4.2: Робота з двійковими числами

У розділі 7 ми розглянемо кілька перетворювачів для підрахунку фотонів. Перетворювачі виготовлені з масиву - деякі використовують лінійний масив, а деякі використовують двовимірний масив - окремих одиниць виявлення. Ми будемо турбуватися про подробиці того, як працюють ці перетворювачі в розділі 7, але якщо ви швидко подивитеся на рис. 7.5.4 - 7.5.6, ви побачите, що кількість окремих одиниць виявлення цікава: лінійний масив 1024 окремих одиниць; інший лінійний масив, але з 2048 одиницями, і двовимірний масив, який має\(1024 \times 1024 = 1,048,576\) окремі одиниці. Що цікаво в цих числах, так це те, що кожен - це сила двох:\(1024 = 2^{10}\),\(2048 = 2^{11}\), і\(1,048,576 = 10^{20}\).

Людям зручно працювати з числами, вираженими за допомогою десяткового позначення, яке спирається на 10 унікальних цифр (0, 1, 2, 3, 4, 5, 6, 7, 8 і 9), але комп'ютери працюють з інформацією, використовуючи двійкові позначення, які обмежені лише двома унікальними цифрами (0 і 1). Хоча ми не будемо завершувати обчислення за допомогою двійкових чисел, ви побачите приклади інструментальних методів, таких як FT-ЯМР, де алгоритми аналізу даних (перетворення Фур'є в даному випадку) вимагають, щоб кількість точок даних була степеню дві. Тому корисно ознайомитися з тим, як ми представляємо числа як в десятковій, так і в двійковій формі.

Десяткове представлення чисел

Мій університет був заснований в 1837 році, який є десятковим виразом року. Кожна з цих чотирьох цифр являє собою силу 10, факт, який зрозумілий, коли ми читаємо число вголос: тисяча - вісімсот - тридцять - сім, або, коли ми записуємо його таким чином

\[(1 \times 1000) + (8 \times 100) + (3 \times 10) + (7 \times 1) = 1837 \nonumber \]

або таким чином

\[(1 \times 10^3) + (8 \times 10^2) + (3 \times 10^1) + (7 \times 10^0) = 1837 \nonumber \]

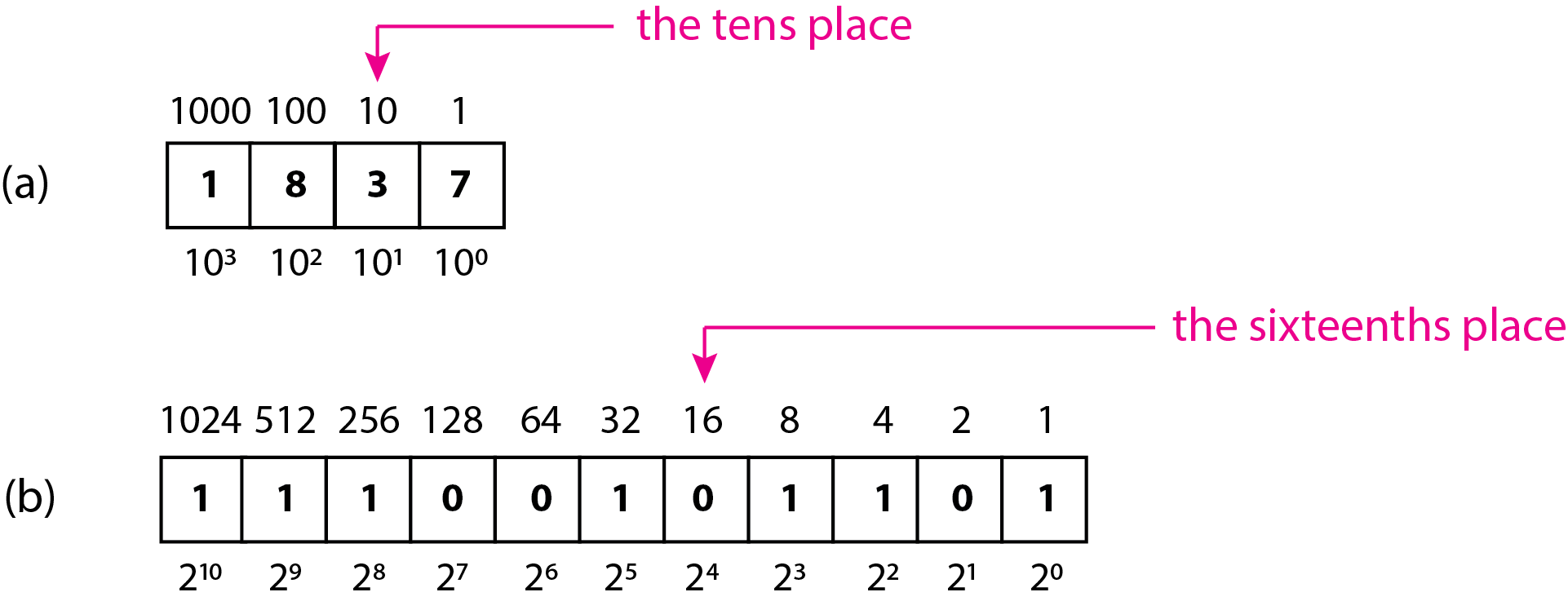
Ми маємо на увазі 7, що знаходяться в одному місці (\(10^0 = 1\)), 3 в десятках місце (\(10^1 = 10\)), 8 у сотні місце (\(10^2 = 100\)), і 1 в тисячних місце (\(10^3 = 1000\)). \(\PageIndex{1}a\)На малюнку показані ці три способи представлення числа за допомогою десяткового позначення.

Малюнок\(\PageIndex{1}\). Три позначення, що використовуються для представлення числа, використовуючи (а) десяткові цифри та степені 10 та (b) двійкові цифри та степені 2. Однакове число представлено як в (a), так і (b).

Двійкове представлення чисел

Десяткове число 1837 - це 11100101101 в двійковій системі числення. Ми бачимо, що це правда, якщо ми дотримуємося шаблону для десяткових чисел у зворотному напрямку. Є одинадцять двійкових цифр, тому ми починаємо з вираження числа у вигляді кратних степеням двох від\(2^{10}\) до\(2^{0}\), починаючи з цифри найдалі вліво і рухаючись вправо

\[(1 \times 2^{10}) + (1 \times 2^{9}) + (1 \times 2^{8}) + (0 \times 2^{7}) + (0 \times 2^{6}) + (1 \times 2^{5}) + (0 \times 2^{4}) + (1 \times 2^{3}) + (1 \times 2^{2}) + (0 \times 2^{1}) + (1 \times 2^{0}) = 1837 \nonumber \]

Кожна сила двох має десятковий еквівалент -\(2^4\) це те ж саме, що\(2 \times 2 \times 2 \times 2 = 16\), наприклад, - який ми можемо висловити тут як

\[(1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Кожна сила двох також представляє місце; таким чином, другий 0 праворуч знаходиться в шістнадцятому місці. Малюнок\(\PageIndex{1}b\) надає наочне уявлення цих способів вираження двійкового числа.

Перетворення між десятковими та двійковими уявленнями чисел

Існує безліч он-лайн калькуляторів, які ви можете використовувати для перетворення між десятковими та двійковими уявленнями чисел, наприклад, тут. Тим не менш, корисно бути зручним з перетворенням чисел вручну. Перетворення двійкового числа в десятковий еквівалент є простим, як ми показали вище для двійкового представлення року, в якому був заснований мій університет

\[11100101101 = (1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Перетворення десяткового числа, такого як 1837, в його двійковий еквівалент вимагає трохи більше роботи; Таблиця\(\PageIndex{1}\) допоможе нам організувати перетворення. Ми починаємо з написання дивіденду, який становить 1837 рік, у крайньому лівому стовпці і ділимо його на 2, записуючи частку 918 у другому стовпці, а залишок 1 у третьому стовпці; зауважте, що ділення на 2 дає залишок 0, якщо дивіденд парний або залишок 1, якщо дивіденд непарний. Залишок - показник для першого місця в двійковій системі числення. В даному випадку у нас є\(2^0 = 1\). Коефіцієнт стає дивідендом для наступного циклу, при цьому процес триває, поки ми не досягнемо частки 0. Двійковий еквівалент початкового десяткового числа задається читанням залишків від низу до верху як 11100101101.

Таблиця\(\PageIndex{1}\). Перетворення двійкового числа в десятковий еквівалент.

дивідендів	частка	залишок	двійкові позначення
1837	918	1	\(2^0 = 1\)
918	459	0	\(2^1 = 1\)
459	229	1	\(2^2 = 1\)
229	114	1	\(2^3 = 1\)
114	57	0	\(2^4 = 1\)
57	28	1	\(2^5 = 1\)
28	14	0	\(2^6 = 1\)
14	7	0	\(2^7 = 1\)
7	3	1	\(2^8 = 1\)
3	1	1	\(2^9 = 1\)
1	0	1	\(2^{10} = 1\)