5: Тестування гіпотез
- Page ID
- 97447
З початку тексту було підкреслено, що першочерговим приводом для ведення статистики є прийняття рішення. Кращі рішення можуть бути прийняті, якщо вони базуються на найкращих наявних доказах. Хоча ідеальною ситуацією було б отримання даних від усього населення, реальність така, що дані майже завжди надходитимуть із вибірки. Оскільки вибіркові дані варіюються залежно від випадкового процесу, який використовувався для його вибору, дослідник змушений використовувати вибіркові дані, щоб зробити висновок про всю сукупність. Це умовивід. Він використовує конкретні часткові докази, щоб зробити більш загальний висновок.
У главі 5 були розроблені формули для перевірки гіпотез про пропорції і засоби. У першому випадку формула була
\[z = \dfrac{\hat{p} - p}{\dfrac{p(1 - p)}{n}}\]
і в останньому випадку це було
\[z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}.\]
Загалом, ці формули генерують тестову статистику z, яка використовується для визначення кількості стандартних помилок, з яких є статистика. Нормальний розподіл потім використовується для визначення ймовірності отримання цієї статистики або більш екстремальної статистики. Ця ймовірність називається p-значенням.
Кожне число, необхідне для використання формули
\[z = \dfrac{\hat{p} - p}{\dfrac{p(1 - p)}{n}}\]
можна знайти в нульовій гіпотезі (p) або за даними (\(\hat{p}\),\(n\)). Те ж саме не можна сказати і про формулу
\[z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}.\]
Хоча значення для\(\mu\) походить від нульової гіпотези,\(\bar{x}\) а значення і n походять з вибіркових даних, немає можливості отримати значення\(\sigma\) без проведення перепису. В останньому розділі вам завжди говорили значення\(\sigma\), але цього не відбувається в реальному світі, тому що для пошуку\(\sigma\) потрібно спочатку знайти,\(\mu\) і якби ви знали\(\mu\), не було б підстав перевіряти гіпотезу про це.
Вирішення цієї проблеми вимагає двох змін до процесу, який використовувався в попередньому розділі. Перша зміна полягає в тому, що нам доведеться оцінити\(\sigma\). Найкраща оцінка - s, стандартне відхилення вибірки. Заміна\(\sigma\) на s означає, що ми більше не можемо використовувати стандартний нормальний розподіл (z розподіл). Друга зміна, отже, полягає у пошуку більш відповідного розподілу, який може бути використаний для моделювання розподілу засобів вибірки.
Набір розподілів, званих t розподілами, використовується, коли стандартна похибка середнього,\(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\) замінюється розрахунковою стандартною похибкою середнього\(s_{\bar{x}} = \dfrac{s}{\sqrt{n}}\). Формула z для засобів,
\[z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}\]
потім модифікується, щоб стати формулою t
\[t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}.\]
Зверніть увагу, єдина різниця полягає у використанні s замість\(\sigma\). Розподіли t використовуються, оскільки вони забезпечують кращу апроксимацію розподілу вибіркових засобів, коли стандартне відхилення населення повинно бути оцінено за допомогою стандартного відхилення вибірки.
На відміну від нормального розподілу, існує багато розподілів t, кожен з яких визначається кількістю ступенів свободи. Ступені свободи - це нове поняття, яке вимагає невеликого пояснення.
Поняття ступенів свободи пов'язане з кількістю незалежних значень, які можуть ідентифікувати позицію. Це може бути простіше подумати, якщо ви зображуєте декартову систему координат. З будь-якими двома незалежно вибраними значеннями, які зазвичай називаються x та y, позиція точки може бути розташована десь на графіку. Отже, точка, яка підібрана, має два ступені свободи. Однак якщо на точках ставиться обмеження, наприклад x + y = 3, то тільки одне з значень може бути незалежним, а інше значення буде залежати від незалежного значення. Через обмеження одна ступінь свободи була втрачена, тому тепер точка має лише один ступінь свободи. Якщо на систему ставиться друге обмеження, наприклад x — y = 1, то інший ступінь свободи втрачається. Ступені свободи втрачаються кожного разу, коли застосовується обмеження.
Для вибіркових даних кожне значення являє собою новий доказ, за умови, що дані є незалежними. Залежні дані штучно завищують розмір вибірки, не надаючи більше інформації. Оскільки більший розмір вибірки призведе до меншої стандартної помилки, яка призведе до більшого значення t і, отже, збільшить шанс статистично значущого висновку, то важливо лише підрахувати кількість незалежних значень даних, які відомі як ступені свободи. Один ступінь свободи втрачається щоразу, коли параметр замінюється статистикою. Тому, коли стандартна помилка\(\sigma_{bar{x}} = \dfrac{\sigma}{\sqrt{n}}\) стає розрахунковою стандартною похибкою\(s_{\bar{x}} = \dfrac{s}{\sqrt{n}}\), втрачається одна ступінь свободи. У цьому випадку df = n — 1, де df - абревіатура ступенів свободи.
Формула для генерації тестової статистики, t, яка використовується для визначення кількості стандартних похибок вибіркового середнього від гіпотезованого середнього
\[t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}\]
Він має n-1 ступінь свободи.
Так само, як z = 1 являє собою 1 стандартне відхилення вище середнього для нормального розподілу,\(t = 1\) являє собою 1 стандартне відхилення вище середнього в розподілі t. Після того, як значення\(t\) було визначено, p-значення можна знайти, заглянувши в таблицю t.
Студентські дистрибутиви
| Ймовірність одного хвоста | 0.4 | 0,25 | 0.1 | 0,05 | 0,025 | 0,01 | 0,005 | 0,0005 |
| Ймовірність двох хвостів | 0.8 | 0.5 | 0.2 | 0.1 | 0,05 | 0,02 | 0,01 | 0,001 |
| Рівень довіри | 20% | 50% | 80% | 90% | 95% | 98% | 99% | 99,9% |
| дф | ||||||||
| 1 | 0,325 | 1.000 | 3.078 | 6.314 | 12.706 | 31.821 | 63.656 | 636.578 |
| 2 | 0,289 | 0,816 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 31.600 |
| 3 | 0,277 | 0,765 | 1,638 | 2.353 | 3.182 | 4.541 | 5.841 | 12.924 |
| 4 | 0,271 | 0,741 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 8.610 |
| 5 | 0,267 | 0,727 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 6.869 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2.447 | 3.143 | 3.707 | 5.959 |
| 7 | 0,263 | 0,711 | 1.415 | 1,895 | 2.365 | 2.998 | 3.499 | 5.408 |
| 8 | 0,262 | 0.706 | 1.397 | 1,860 | 2.306 | 2.896 | 3.355 | 5.041 |
| 9 | 0,261 | 0.703 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.781 |
| 10 | 0,260 | 0,700 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.587 |
| 11 | 0,260 | 0.697 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 4.37 |
| 12 | 0,259 | 0,695 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 4.318 |
| 13 | 0,259 | 0.694 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 4.221 |
| 14 | 0,258 | 0.692 | 1,345 | 1.761 | 2.145 | 2.624 | 2.97 | 4.140 |
| 15 | 0,258 | 0.691 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 4.073 |
| 16 | 0,258 | 0.690 | 1,337 | 1.746 | 2.120 | 2.583 | 2.921 | 4.015 |
| 17 | 0,257 | 0.689 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3,965 |
| 18 | 0,257 | 0.689 | 1,330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.922 |
| 19 | 0,257 | 0.688 | 1,328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.883 |
| 20 | 0,257 | 0.687 | 1.325 | 1,725 | 2.086 | 2.528 | 2.845 | 3.850 |
| 21 | 0,257 | 0.686 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.819 |
| 22 | 0,256 | 0.686 | 1.321 | 1.717 | 2.074 | 2.608 | 2.819 | 3.792 |
| 23 | 0,256 | 0.685 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.768 |
| 24 | 0,256 | 0.685 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.745 |
| 25 | 0,256 | 0,684 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.745 |
| 26 | 0,256 | 0,684 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.707 |
| 27 | 0,256 | 0,684 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.689 |
| 28 | 0,256 | 0.683 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.674 |
| 29 | 0,256 | 0.683 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.660 |
| 30 | 0,256 | 0.683 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.646 |
| 40 | 0,255 | 0.681 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 3.551 |
| 60 | 0,254 | 0.679 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.460 |
| 120 | 0,254 | 0.677 | 1.289 | 1.658 | 1,980 | 2.358 | 2.617 | 3.373 |
| \(z^{\ast}\) | 0,253 | 0.674 | 1.282 | 1,645 | 1,960 | 2.326 | 2.576 | 3.290 |
Припущення при використанні t розподілів з малим розміром вибірки полягає в тому, що вибірка береться з нормально розподіленої сукупності. Хоча деякі дослідники вважають, що ця тестова статистика є достатньо надійною, щоб терпіти деяке порушення цього припущення, як мінімум, слід переглянути гістограму даних, щоб побачити, чи здається припущення реалістичним. Якщо цього не відбувається, повинні бути переслідувані інші методи аналізу, не обговорювані в цьому тексті.
Спосіб використання цієї таблиці t для визначення p-значення полягає в тому, щоб спочатку знайти рядок з відповідною кількістю ступенів свободи. У цьому рядку знайдіть діапазон, який буде містити статистику тесту. Переміщайтеся до першого ряду, якщо ви робите тест з одним хвостом або другого ряду, якщо це тест на два хвоста. Далі визначте місце розташування альфа. Якщо ваше p-значення більше альфа, то використовуйте символ нерівності, щоб показати, що. Якщо ваше p-значення менше альфа, то покажіть, що з символом нерівності. Якщо може бути передбачена більша деталізація, вона повинна бути. Оскільки розподіли t симетричні, негативні значення t можна знайти в цій таблиці, ігноруючи негативні знаки і припускаючи, що області в першому рядку знаходяться ліворуч. Нижче наведено 2 приклади. Знак в альтернативній гіпотезі, рівень значущості, ступені свободи і значення t наводяться в кожному прикладі.
1. \(H_1: > \)\(\alpha = 0.05\)дф = 6, т = 2,3
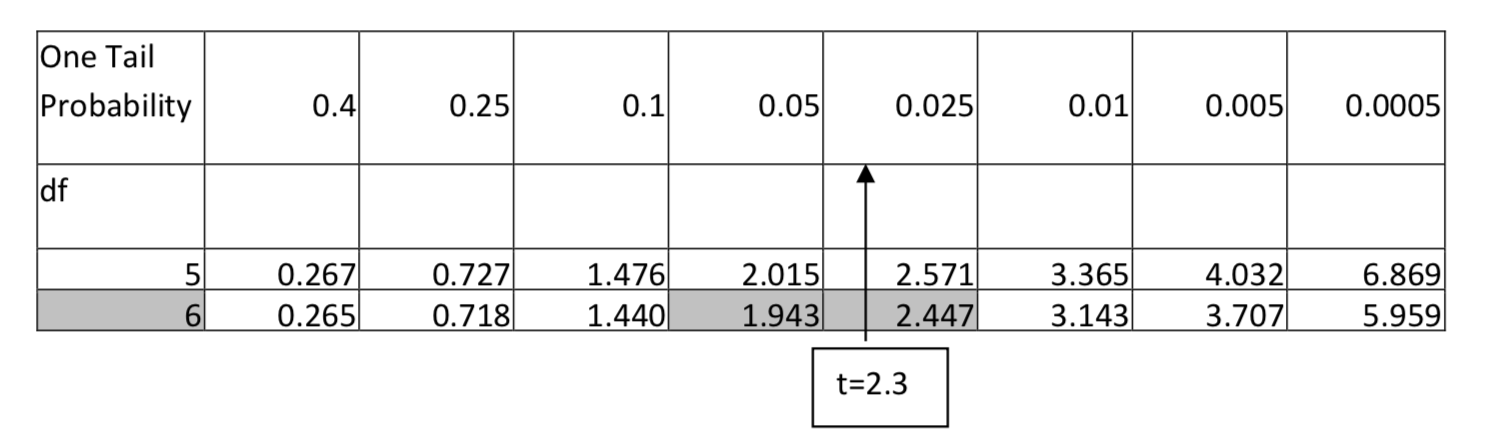
Для 6 ступенів свободи 2,3 падає між 1,943 і 2,447, що означає, що він має площу в хвості, яка знаходиться між 0,05 і 0,025. Значення p буде повідомлено як p < 0,05.
2. \(H_1: \ne \)\(\alpha = 0.01\)дф = 18, т = -1,26
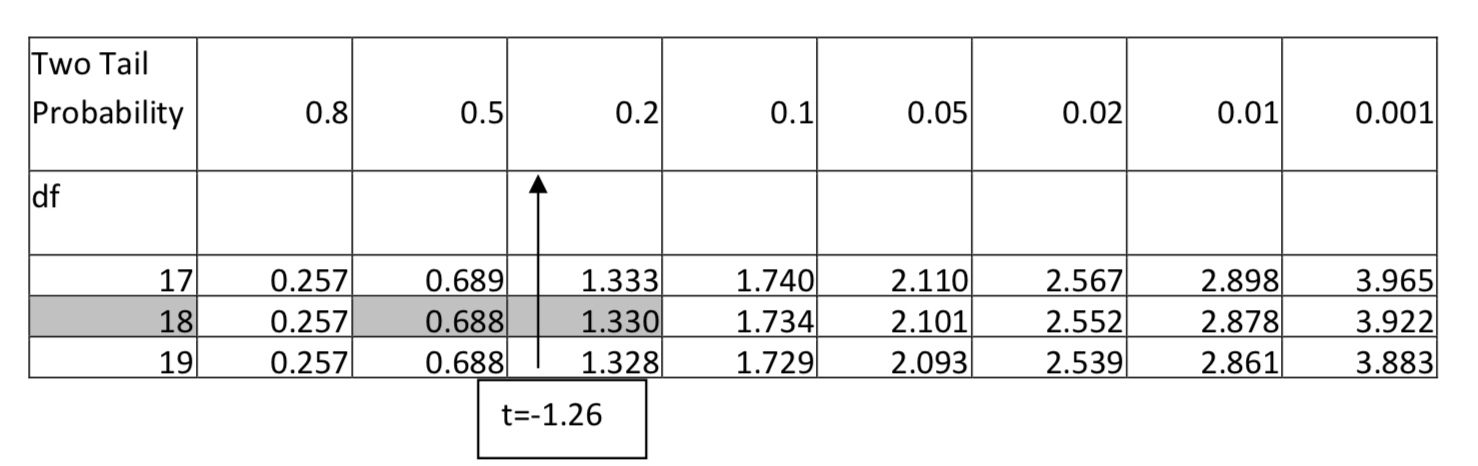
Для 18 ступенів свободи -1,26 падає між 0,688 і 1,328, якщо негативний знак ігнорується, тому площа в двох хвостах падає між 0,5 і 0,2. Оскільки будь-яке значення в цьому діапазоні не було б значним на рівні 0,01, то p-значення більше 0,01. Однак більшу деталізацію можна надати, вказавши p-значення більше 0,2. Було б неправильно сказати, що p-значення менше 0,5, тому що це не говорить нам, чи воно більше або менше 0,01.
Є два різних інференційних підходи, які можуть бути прийняті. Протягом більшої частини цього тексту основна увага приділялася концепції тестування гіпотез. Це означає, що насправді існує гіпотеза про те, що було б знайдено з перепису. Альтернативний інференційний підхід виникає тоді, коли немає гіпотези. У таких випадках мета полягає в тому, щоб оцінити параметр, а не визначити, чи є гіпотеза про нього правильною. Оскільки вся увага книги була зосереджена на тестуванні гіпотез, ми почнемо там, а потім розглянемо ідею оцінки параметра в наступному розділі. Існує значна кількість ситуацій тестування гіпотез і формул, але ми зупинимося лише на чотирьох з них у цій главі, а потім додамо ще кілька в наступних розділах. Пояснення буде надано з обговоренням вправи.
Брифінг 5.1 Вправа
Уряд США рекомендує людям отримувати 2,5 години помірно-інтенсивних аеробних вправ щотижня або 1,25 годин енергійно-інтенсивних вправ щотижня разом з деякими силовими тренуваннями, такими як ваги або віджимання. Вправи допомагають знизити ризик діабету, серцевих захворювань, деяких видів раку та покращують психічне здоров'я. (www.cbsnews.com/8301-204_162-... потрібна вправа/)
Чотири формули тестування гіпотез, які будуть показані в цьому розділі, будуть проілюстровані цими п'ятьма питаннями. Коли ви читаєте питання, спробуйте визначити будь-які подібності або відмінності між ними, оскільки це в кінцевому підсумку допоможе вам, яку формулу слід використовувати.
- Чи є частка людей, які займаються фізичними вправами, достатньою для виконання рекомендацій уряду менше 0,25?
- Чи є частка людей з проблемами зі здоров'ям, такими як діабет, серцеві захворювання або рак, нижча для тих, хто відповідає рекомендаціям уряду щодо фізичних вправ, ніж для тих, хто цього не робить?
- Чи середня кількість вправ, яку студент коледжу робить за тиждень більше 2,5 годин?
- Чи менше середня вага людини після місяця нової регулярної аеробної фітнес-програми?
- Для тих, хто регулярно займається фізичними вправами, середня кількість вправ випускник коледжу робить за тиждень, відрізняється від того, хто не закінчує коледж?
Є дві різні речі, на які слід звернути увагу при визначенні подібності та відмінностей. Перший - чи є параметр, який згадується, середнім або пропорційним. Друге - це кількість популяцій. Наступна таблиця повторює питання, надає цікавить параметр, кількість популяцій і приклад гіпотез.
|
Питання |
Параметр |
Популяції |
Гіпотези |
|
Чи є частка людей, які займаються фізичними вправами, достатньою для виконання рекомендацій уряду менше 0,25? |
пропорція |
1 |
\(H_0: P = 0.25\) |
|
Чи є частка людей з проблемами зі здоров'ям, такими як діабет, серцеві захворювання або рак, нижча для тих, хто відповідає рекомендаціям уряду щодо фізичних вправ, ніж для тих, хто цього не робить? |
пропорція |
2 |
\(H_0: P_{\text{exercise}} = P_{\text{don’t}}\) |
|
Чи середня кількість вправ, яку студент коледжу робить за тиждень більше 2,5 годин? |
маю на увазі |
1 |
\(H_0: \mu = 2.5\) |
|
Чи менше середня вага людини після місяця нової регулярної аеробної фітнес-програми? |
маю на увазі |
1 |
\(H_0: \mu = 0\) |
|
Для тих, хто регулярно займається фізичними вправами, середня кількість вправ випускник коледжу робить за тиждень, відрізняється від того, хто не закінчує коледж? |
маю на увазі |
2 |
\(H_0: \mu_{\text{college grad}} = \mu_{\text{not college grad}}\) |
Категоричні дані знадобляться для питань про пропорції; кількісні дані знадобляться для питань про середнє значення. Коротке пояснення потрібно для четвертого питання. Щоб визначити кількість змін у людини після початку фітнес-програми, необхідно зібрати два набори даних. Людина повинна бути зважений до фітнес-програми, а потім знову після одного місяця. Ці дані залежні, а значить, вони повинні звертатися до однієї і тієї ж особи. Зрештою, дані, які будуть проаналізовані, - це різниця між вагою людини до і після. Тому два значення даних стискаються в одне значення шляхом віднімання. Якщо після мінус-до різниця у вазі дорівнює 0, то змін не відбулося. Якщо вона менше 0, вага була втрачена.
Оскільки докази, які допоможуть вирішити, яка гіпотеза підтверджується даними, будуть надходити з вибірки, і ця вибірка є лише одним з багатьох можливих результатів вибірки, які утворюють нормально розподілений розподіл вибірки, то ми можемо використовувати те, що відомо про розподіл вибірки для визначення ймовірності. що ми вибрали б дані, які ми отримали, або більш екстремальні дані (p-значення).
Незважаючи на теоретичну природу розподілу вибірки, він є джерелом для визначення ймовірностей. Тому ми спочатку визначимо, що містять дистрибутиви та важливі формули, пов'язані з цим розподілом.
Перший раз ми зіткнулися з нормальним розподілом, коли він використовувався як наближення для біноміального розподілу. В даному випадку дані складалися з підрахунків.
Середнє значення цього розподілу знайдено з\(\mu = np\). Стандартне відхилення - це\(\sigma = \sqrt{npq}\). Формула для визначення кількості стандартних відхилень величини становить від середнього значення\(z = \dfrac{x - \mu}{\sigma}\).
Підрахунок врешті-решт перетворили на пропорції, розділивши кількість на розмір вибірки. Розподіл складався з усіх можливих пропорцій зразка.
Розподіл пропорцій зразка має середнє значення\(\mu_{\hat{p}} = p\) і стандартне відхилення\(\sigma_{\hat{p}} = \dfrac{p(1 - p)}{n}\). Формула визначення кількості стандартних відхилень пропорції вибірки становить від середнього значення\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1 - p)}{n}}}\).
Наступного разу ми зіткнулися з нормальним розподілом, коли ми мали кількісні дані, і в цьому випадку розподіл складався з вибіркових засобів.
Середнє значення всіх можливих засобів вибірки є\(\mu_{\bar{x}} = \mu\) і стандартна помилка є\(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\). Формула для визначення кількості стандартних відхилень, яке має середнє значення вибірки від гіпотезованого середнього значення популяції\(z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}\). Оскільки\(\sigma\) невідомо, він оцінюється з s, так що розрахункова стандартна похибка є\(s_{\bar{x}} = \dfrac{s}{\sqrt{n}}\) і формула Z замінюється формулою t де\(t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}\).
Розподіли та формули, які були щойно показані, такі ж, як або схожі на ті, які ви бачили в главі 5, і які підходять для питань 1, 3 та 4. З іншого боку, питання 2 і 5 мають гіпотези на відміну від тих, що зустрічалися раніше, і тому потрібні певні зусилля для визначення відповідних розподілів та їх засобів та стандартних відхилень. Вони базуватимуться на трьох статистичних результатах, які тут не будуть доведені:
1. Середнє значення різниці двох випадкових величин - це різниця середніх.
2. Дисперсія різниці двох незалежних випадкових величин - це сума дисперсій.
3. Різниця двох незалежних нормально розподілених випадкових величин також нормально розподілена. (Аліага, Марта та Бренда Гундерсон. Інтерактивна статистика. Верхня річка Сідло, Нью-Джерсі: Пірсон Прентіс Холл, 2006. Друк.)
Ми почнемо з питання про те, чи є частка людей з такими проблемами зі здоров'ям, як діабет, серцеві захворювання або рак, нижча для тих, хто відповідає рекомендаціям уряду щодо фізичних вправ, ніж для тих, хто цього не робить. Уряд рекомендував рівні і населення, яке не робить, в межах кожної популяції буде виявлена частка людей з проблемами зі здоров'ям. Тест на гіпотезу буде використовуватися для визначення того, чи мають люди, які займаються фізичними вправами на рекомендованих рівнях, менше проблем зі здоров'ям, ніж люди, які цього не роблять.
\(H_0: P_{\text{exercise}} = P_{\text{don't}}\)
\(H_1: P_{\text{exercise}} < P_{\text{don't}}\)
Написання гіпотез таким чином легко інтерпретувати, але алгебраїчна маніпуляція з ними дасть нам деяке уявлення про розподіл, який би використовувався для представлення нульової гіпотези. \(P_{\text{don’t}}\)буде відніматися з обох сторін.
\(H_0: P_{\text{exercise}} - P_{\text{don't}} = 0\)
\(H_1: P_{\text{exercise}} - P_{\text{don't}} < 0\)
Оскільки жоден\(P_{\text{exercise}}\) або не\(P_{\text{don’t}}\) відомий, оскільки це параметри, найкраще, що можна зробити, це оцінити їх за допомогою пропорцій зразка. Тому\(\hat{p}_{exercise}\) буде використовуватися в якості кошторису\(P_{\text{exercise}}\) і\(\hat{p}_{don't}\) буде використовуватися в якості кошторису\(P_{\text{don’t}}\). Тоді\(\hat{p}_{exercise} - \hat{p}_{don't}\) як кошторис для\(P_{\text{exercise}} - P_{\text{don’t}}\).
Розподіл цікавить нас полягає в тому, що складається з різниці між пропорціями вибірки, узагальнено показаної як\(\hat{p}_{A} - \hat{p}_{B}\).
Середнє значення цього розподілу є\(p_A - p_B\) і стандартне відхилення є\(\sqrt{\dfrac{p_{A} (1 - p_{A})}{n_{A}} + \dfrac{p_{B} (1 - p_{B})}{n_{B}}}\). Оскільки єдине, про що відомо\(p_A\) і\(p_B\) це те, що вони рівні, необхідно оцінити їх значення так, щоб фактично можна було обчислити стандартне відхилення. Для цього пропорції зразка будуть об'єднані. Комбінована пропорція визначається як
\[\hat{p}_c = \dfrac{x_A + x_B}{n_A + n_B}.\]
Заміна\(p_A\) і\(p_B\) з\(\hat{p}_c\) результатами в формулі розрахункової стандартної похибки
\[\sqrt{\dfrac{\hat{p}_{c} (1 - \hat{p}_{c})}{n_{A}} + \dfrac{\hat{p}_{c} (1 - \hat{p}_{c})}{n_{B}}} \text{ or } \sqrt{\hat{p}_{c} (1 - \hat{p}_{c}) (\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}})}\]
Тепер ми можемо замінити\(z\) формулу,\(z = \dfrac{x − \mu}{\sigma}\) щоб отримати тестову статистику, яка використовується при тестуванні різниці між двома пропорціями населення,
\[z = \dfrac{(\hat{p}_{A} - \hat{p}_{B}) - (p_{A} - p_{B})}{\sqrt{\hat{p}_{c} (1 - \hat{p}_{c}) (\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}})}}\]
Це можна написати трохи простіше у випадках, коли нульова\(P_A = P_B\) гіпотеза\(p_A – p_B = 0\), що означає, що, так що цей термін може бути усунений, щоб дати статистику тесту.
\[z = \dfrac{(\hat{p}_{A} - \hat{p}_{B})}{\sqrt{\hat{p}_{c} (1 - \hat{p}_{c}) (\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}})}}\]
Для цієї тестової статистики обидва розміри вибірки повинні бути достатньо великими (n> 20) з мінімальним успіхом 5 та 5 невдачами.
Аналогічний підхід буде прийнятий з питанням 4, який запитує, чи середня кількість вправ випускник коледжу робить за тиждень, відрізняється від того, хто не закінчує коледж? Є два населення порівнюються, населення випускників коледжів і населення не- випускників коледжів. Буде порівнюватися середня кількість фізичних вправ у кожній з цих популяцій.
Коли порівнюються засоби двох популяцій, гіпотези пишуться так:
\(H_0: \mu_{\text{college grad}} = \mu_{\text{not college grad}}\)
\(H_1: \mu_{\text{college grad}} \ne \mu_{\text{not college grad}}\)
Написання гіпотез таким чином легко інтерпретувати, але алгебраїчна маніпуляція з ними дасть нам деяке уявлення про розподіл, який би використовувався для представлення нульової гіпотези.
\(\mu_{\text{not college grad}}\)буде відніматися з обох сторін.
\(H_0: \mu_{\text{college grad}} - \mu_{\text{not college grad} = 0}\)
\(H_1: \mu_{\text{college grad}} - \mu_{\text{not college grad} \ne 0}\)
Оскільки\(n\) або\(\mu_{\text{college grad}}\) або\(\mu_{\text{not college grad}}\) відомі, оскільки це параметри, найкраще, що можна зробити, це оцінити їх за допомогою зразкових засобів. Тому\(\bar{x}_{college\ grad}\) буде використовуватися в якості кошторису\(\mu_{\text{college grad}}\) і\(\bar{x}_{college\ grad}\) буде використовуватися в якості кошторису\(\mu_{\text{not college grad}}\). Тоді\(\bar{x}_{college\ grad} - \bar{x}_{not\ college\ grad}\)
Розподіл інтересу для нас полягає в тому, що складається з різниці між вибірковими засобами, узагальнено показаними як\(\bar{x}_{A} - \bar{x}_{B}\).
Середнє значення цього розподілу є\(\mu_A - \mu_B\) і стандартне відхилення є\(\sqrt{\dfrac{\sigma_{A}^{2}}{n_{A}} + \dfrac{\sigma_{B}^{2}}{n_{B}}}\). Ще раз зіткнемося з проблемою, що стандартні відхилення популяцій\(\sigma_A\) і не\(\sigma_B\) відомі, тому їх необхідно оцінювати за допомогою вибірки стандартного відхилення sA і sB. Додатковою проблемою є те, що невідомо, чи однакові відхилення для двох популяцій (однорідні). Нерівні дисперсії (гетерогенні) збільшують коефіцієнт помилок типу I. (Шескін, David J. Довідник параметричних та непараметричних статистичних процедур. Бока-Ратон: Чепмен і Холл/CRC, 2000. Друк.)
\(t\)Тест для двох незалежних зразків використовується для перевірки гіпотези. Цей тест залежить від наступних припущень.
- Кожен зразок вибирається випадковим чином з популяції, яку він представляє.
- Розподіл даних в популяції, з якої була проведена вибірка, нормальний.
- Розбіжності двох популяцій рівні. Це однорідність дисперсійного припущення. (Шескін, David J. Довідник параметричних та непараметричних статистичних процедур. Бока-Ратон: Чепмен і Холл/CRC, 2000. Друк.)
Статистика тесту слідує тій же базовій схемі, що й інші тести, яка передбачає знаходження кількості стандартних помилок, які статистика знаходиться далеко від гіпотезованого параметра.
\[t = \dfrac{(\bar{x}_{A} - \bar{x}_{B}) - (\mu_A - \mu_B)}{\sqrt{\dfrac{s_{1}^{2}}{n_1} + \dfrac{s_{2}^{2}}{n_2}}}\]
Припущення з цією формулою полягає в тому, що два розміри вибірки рівні. Якщо ця формула використовується, коли розміри вибірки не рівні, підвищується ймовірність зробити помилку типу I. У таких випадках використовується альтернативна формула, яка включає середньозважене значення оціночних відхилень населення двох груп. Середньозважене значення базується на кількості ступенів свободи в кожному зразку. Цю формулу можна використовувати як для рівних, так і для нерівних розмірів вибірки.
\[t = \dfrac{(\bar{x}_{A} - \bar{x}_{B}) - (\mu_A - \mu_B)}{\sqrt{[\dfrac{(n_A - 1)s_{A}^{2} + (n_B - 1)s_{B}^{2}}{n_A + n_B - 2}][\dfrac{1}{n_A} + \dfrac{1}{n_B}]}}\]
Оскільки два параметри (\(\sigma_A\)і\(\sigma_B\)) замінюються на\(s_A\) і\(s_B\), втрачаються два ступені свободи. Таким чином, кількість ступенів свободи для цієї тестової статистики є\(n_1 + n_2 - 2\).
У цьому розділі представлено чотири різних тести гіпотез. Гіпотези та статистика тестів зведені в наступній таблиці.
| Пропорції (для категоричних даних) | Засоби (для кількісних даних) | |
| 1 - зразок | \(H_0: p = p_0\) \(H_1: p < p_0\)або\(p > p_0\) або\(p \ne p_0\) \(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1 - p)}{n}}}\) припущення: \(np \ge 5, n(1 - p) \ge 5\) |
\(H_0: \mu = \mu_0\) \(H_1: \mu < \mu_0\)або\(\mu > \mu_0\) або\(\mu \ne \mu_0\) \(t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}\) df = n - 1 Припущення: Якщо\(n < 30\), населення приблизно нормально розподілено. |
| 2 - зразки | \(H_0: p_A = p_B\) \(H_1: p_A < p_B\)\(p_A > p_B\)або\(p_A \ne p_B\) \(z = \dfrac{(\hat{p}_{A} - \hat{p}_{B}) - (p_{A} - p_{B})}{\sqrt{\hat{p}_{c} (1 - \hat{p}_{c}) (\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}})}}\) де\(\hat{p}_c = \dfrac{x_A + x_B}{n_A + n_B}\) Припущення: \(np \ge 5\),\(n(1 - p) \ge 5\) для обох популяцій |
\(H_0: \mu_A = \mu_B\) \(H_1: \mu_A < \mu_B\)або\(\mu_A > \mu_B\) або\(\mu_A \ne \mu_B\) \(t = \dfrac{(\bar{x}_{A} - \bar{x}_{B}) - (\mu_A - \mu_B)}{\sqrt{[\dfrac{(n_A - 1)s_{A}^{2} + (n_B - 1)s_{B}^{2}}{n_A + n_B - 2}][\dfrac{1}{n_A} + \dfrac{1}{n_B}]}}\) df =\(n_A + n_B - 2\) Припущення: Якщо\(n < 30\), населення приблизно нормально розподіляється. |
Для кожної ситуації тестування гіпотез вам доведеться вирішити, яку формулу і яку таблицю використовувати. Зверніть увагу, що коли гіпотези стосуються пропорцій, використовується стандартний нормальний\(z\) розподіл. Коли гіпотези стосуються засобів, використовуються t розподіли.
Тепер ми повернемося до наших початкових п'яти питань. Статистика, наведена в цій проблемі, є фіктивною.
- Чи є частка людей, які займаються фізичними вправами, достатньою для виконання рекомендацій уряду менше 0,25?
Припустимо, що була взята випадкова вибірка 800 дорослих. З них 184 стверджували, що вони відповідали рекомендації уряду щодо здійснення. Чи можемо ми зробити висновок, що частка, яка відповідає цій рекомендації, становить менше 25%? Використовуйте рівень значущості 0,05.
Гіпотези:
\(H_0: p = 0.25\)
\(H_1: p < 0.25\)
Пропорція\(\bar{p} = \dfrac{x}{n} = \dfrac{184}{800} = 0.23\)
вибірки є Статистика тесту є\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1 - p)}{n}}}\). З заміною\(z = \dfrac{0.23 - 0.25}{\sqrt{\dfrac{0.25(1 - 0.25)}{800}}} = -1.31\)
Перевірте стандартну нормальну таблицю розподілу, щоб знайти область зліва 0.0951. Це p-значення, тому що напрямок крайності - вліво. Оскільки p-значення більше рівня значущості, дані узгоджуються з нульовою гіпотезою. Робимо висновок, що при рівні 0,05 значущості частка дорослих, які відповідають державним рекомендаціям щодо фізичних вправ, не значно менше 25% (\(z\)= -1,31,\(p\) = 0,0951,\(n\) = 800). - Чи є частка людей з проблемами зі здоров'ям, такими як діабет, серцеві захворювання або рак, нижча для тих, хто відповідає рекомендаціям уряду щодо фізичних вправ, ніж для тих, хто цього не робить?
Припустимо, що випадкова вибірка взята з обох популяцій. Для людей, які відповідають рекомендованій кількості фізичних вправ, 84 з 560 мали проблеми зі здоров'ям. Для людей, які недостатньо займалися фізичними вправами, 204 з 850 мали проблеми зі здоров'ям.
Гіпотези:
\(H_0: P_{\text{exercise}} = P_{\text{don't}}\)
\(H_1: P_{\text{exercise}} < P_{\text{don't}}\)
Пропорції вибірки є\(\hat{p}_{exercise} = \dfrac{x}{n} = \dfrac{84}{560} = 0.15\) і\(\hat{p}_{don't} = \dfrac{x}{n} = \dfrac{204}{850} = 0.24\)
об'єднана пропорція є \(\hat{p}_{c} = \dfrac{x_{A} + x_{B}}{n_{A} + n_{B}} = \dfrac{84 + 204}{560 + 850} = 0.204\)
Тестова статистика\(z = \dfrac{(\hat{p}_{A} - \hat{p}_{B}) - (p_{A} - p_{B})}{\sqrt{\hat{p}_{c} (1 - \hat{p}_{c}) (\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}})}}\)
з заміною\(z = \dfrac{(0.15 - 0.24)}{\sqrt{0.204(1 - 0.204) (\dfrac{1}{560} + \dfrac{1}{850})}} = -4.10\)
Перевірка стандартної нормальної таблиці розподілу,\(z\) значення -4.10 нижче найнижчого значення в таблиця (-3.49) тому площа в лівому хвості менше 0,0002. Ми робимо висновок, що на рівні 0,05 значення частка проблем зі здоров'ям для людей, які відповідають рекомендаціям уряду щодо фізичних вправ, значно менша, ніж для людей, які не займаються цим великим навантаженням (\(z\)= -4.10, p < 0.0002,\(n_{\text{exercise}}=560\),\(n_{\text{don’t}} = 850\)). - Чи середня кількість вправ, яку студент коледжу робить за тиждень більше 2,5 годин?
Для цього питання докази, які потрібно зібрати, - це години фізичних вправ за тиждень. Тобто кількісні дані. Щоб скористатися t-test, нам потрібно переконатися, що дані в вибірці приблизно нормально розподілені. Гіпотези, які будуть перевірені, такі:
\(H_0: \mu = 2.5\)
\(H_1: \mu > 2.5\)
Рівень значущості - 0,10.
Кількість годин вправ по 20 випадково відібраним учням наведено в таблиці нижче.3.7 2 7.1 1.7 0 0 2.1 2.9 4 3.2 3.4 1.3 1 4.2 0 1.3 2.9 5.3 4.4 2.3 Гістограма для цих даних показує, що вона приблизно нормально розподілена. Найбільше відхилення від нормальності знаходиться в лівому хвості, оскільки неможливо здійснювати менше 0 годин на тиждень.
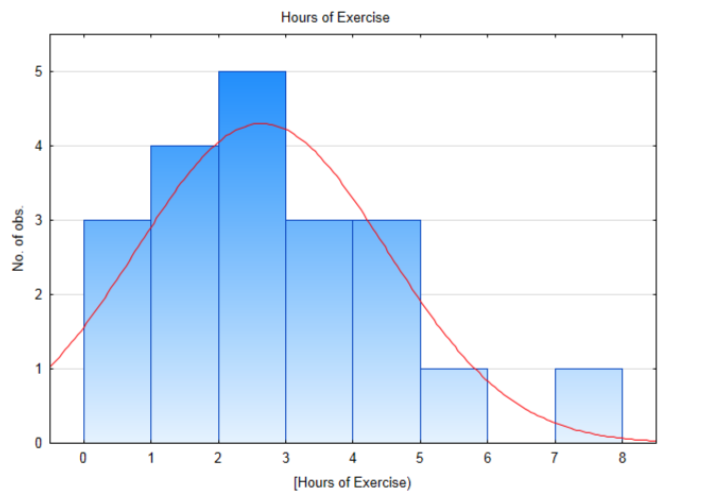
Середнє значення зразка та стандартне відхилення - 2,64 години та 1,855 годин відповідно. Статистика тесту така:\(t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}\), з підміною,\(t = \dfrac{2.64 - 2.5}{\dfrac{1.855}{\sqrt{20}}}\). Після спрощення t = 0,338. Існує 19 ступенів свободи (20 — 1). Скористайтеся таблицею t, в рядку з 19 ступенями свободи знайдіть розташування 0,338. Витяг з таблиці наведено нижче. Зверніть увагу, що 0.338 падає між 0,257 і 0,688, отже, таблиця показує, що область в правому хвості знаходиться між 0,25 і 0,40. Оскільки рівень значущості дорівнює 0,1, а оскільки площа в хвості більше 0,1 і більш конкретно більше 0,25, ми б повідомили, що p-значення більше 0,25.
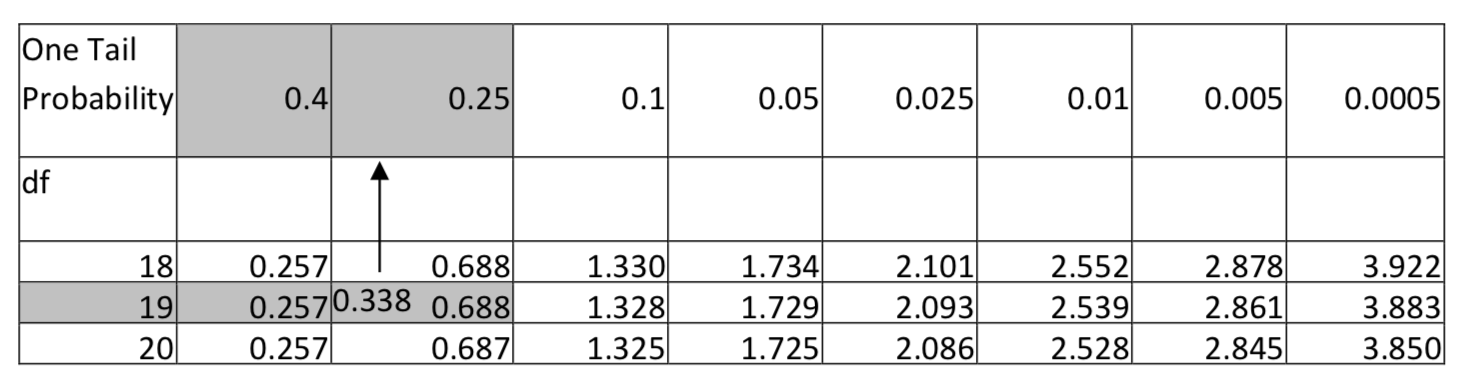
Висновок: при рівні значущості 0,10 середній час, який студенти коледжу здійснюють, не значно перевищує 2,5 години (\(t\)= 0,338,\(p\) > 0,25,\(n\) = 20). - Чи менше середня вага людини після місяця нової регулярної аеробної фітнес-програми?
Для цього питання необхідно зібрати два набори даних, до ваги і після ваги. До ваги буде відніматися від ваги після, щоб визначити зміну ваги. Оскільки в кінцевому підсумку буде тільки один набір даних, буде використаний тест t для одного середнього популяції.
\(H_0: \mu = 0\)
\(H_1: \mu < 0\)
Рівень значущості - 0,10.Предмет 1 2 3 4 5 6 7 8 9 До ваги 158 213 142 275 184 136 172 263 205 Після ваги 154 213 135 278 180 134 171 258 199 Після того, як -4 0 -7 3 -4 -2 -1 -5 -6 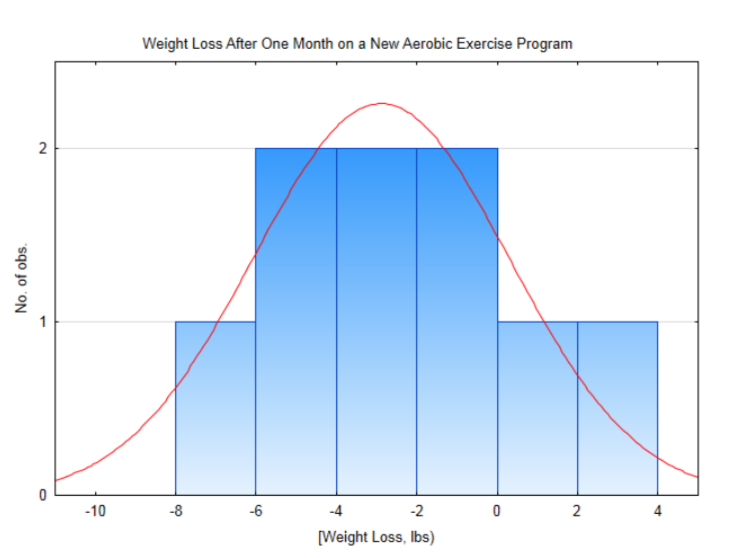
Цей розподіл приблизно нормальний, тому доречно використовувати t-тест для одного середнього популяції. Середнє значення зразка становить -2,89 фунтів зі стандартним відхиленням 3,18 фунтів. статистика випробувань:\(t = \dfrac{\bar{x} - \mu}{\dfrac{s}{\sqrt{n}}}\), з заміною,\(t = \dfrac{-2.89 - 0}{\dfrac{3.18}{\sqrt{9}}}\). Після спрощення t = -2,726. Існує 8 ступенів свободи (9-1). Оскільки -2.726 припадає між 2,306 і 2,896 в ряду для 8 ступенів свободи і так як рівень значущості дорівнює 0,1 але площа в хвості зліва від -2.726 менше 0,025, то висновок полягає в тому, що нова вага значно менше початкової ваги (\(t\)= -2,726,\(p\) < 0,025,\(n\) = 9). Робимо висновок, що люди схудли.
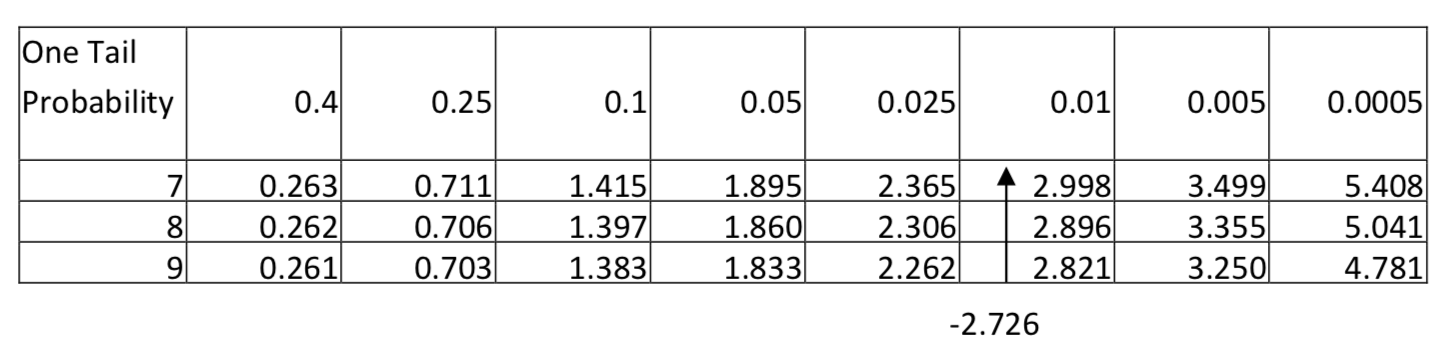
- Для тих, хто регулярно займається фізичними вправами, середня кількість вправ випускник коледжу робить за тиждень, відрізняється від того, хто не закінчує коледж?
Припустимо, що випадкова вибірка береться для населення випускників коледжів, які регулярно займаються фізичними вправами, і інша випадкова вибірка береться з населення не-випускників, які регулярно займаються фізичними вправами. Також припустимо, що кількість вправ зазвичай розподіляється для обох груп і що дисперсія однорідна. Гіпотези наведені нижче. Використовуйте рівень значущості 0,05.
\(H_0: \mu_{\text{college grad}} = \mu_{\text{not college grad}}\)
\(H_1: \mu_{\text{college grad}} \ne \mu_{\text{not college grad}}\)
У таблиці нижче наведено середнє значення, стандартне відхилення та розмір вибірки для двох зразків.Одиниці виміру: години/тиждень Випускники коледжу Не випускний коледж Середнє 4.2 3.8 Стандартне відхилення 1.3 1.2 Розмір вибірки,\(n\) 12 16 Різниця в розмірі вибірки означає, що нам потрібна тестова статистика формула:
\(t = \dfrac{(\bar{x}_{A} - \bar{x}_{B}) - (\mu_A - \mu_B)}{\sqrt{[\dfrac{(n_A - 1)s_{A}^{2} + (n_B - 1)s_{B}^{2}}{n_A + n_B - 2}][\dfrac{1}{n_A} + \dfrac{1}{n_B}]}}\)
яка використовується для незалежних популяцій. Підстановка в формулу дає:
\(t = \dfrac{(4.2 - 3.8) - (0)}{\sqrt{[\dfrac{(12 - 1) 1.3^{2} + (16 - 1) 1.2^{2}}{12 + 16 - 2}][\dfrac{1}{12} + \dfrac{1}{16}]}} = 0.842\)
Через знак нерівності в альтернативній гіпотезі це двоххвостий тест. Тестова статистика 0,842 дає p-значення між 0,5 і 0,8. Оскільки це явно вище рівня значущості, то робиться висновок, що на рівні 0,05 значущості кількість вправ для випускників коледжів істотно не відрізняється від суми для невипускників (\(t\)= 0,842,\(p\) > 0,5,\(n_{\text{college grads}} =12\),\(n_{\text{not college grads}} =16\)). 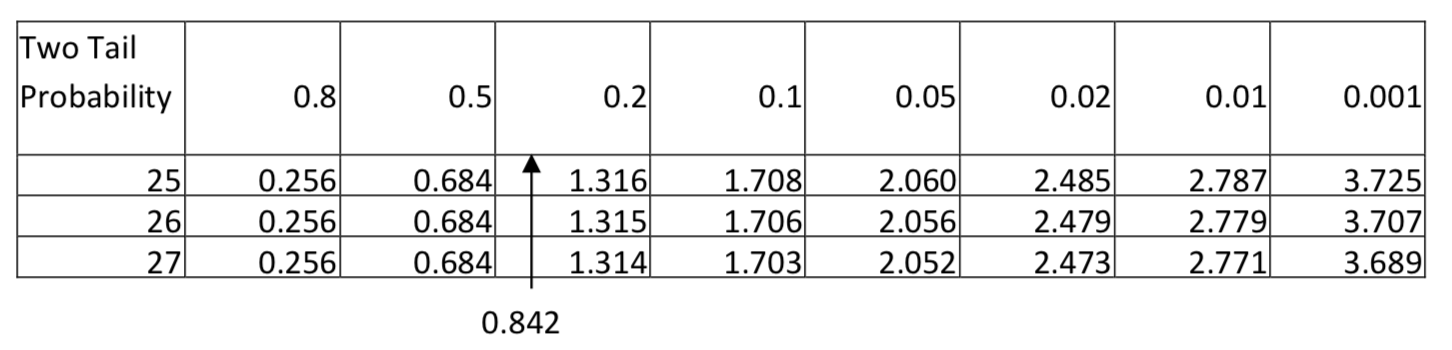
Т-тест для двох незалежних зразків був заснований на припущенні однорідності дисперсії. Існують тести, щоб визначити, чи є дисперсія однорідною, і зміни, які можуть бути внесені до ступенів свободи, якщо це не так.
Всі ці тести можна зробити за допомогою калькулятора TI84. Тести знаходять, вибравши клавішу STAT, а потім за допомогою стрілок курсора рухатися вправо до TESTS.
| Пропорції (для категоричних даних) | Засоби (для кількісних даних) | |
| 1 - зразок | \(H_0: p = p_0\) \(H_1: p < p_0\)або\(p > p_0\) або\(p \ne p_0\) тест 5:1- PropzTest |
\(H_0: \mu = \mu_0\) \(H_1: \mu < \mu_0\)або\(mu > \mu_0\) або\(mu \ne \mu_0\) тест 2: T- тест |
| 2 - зразки | \(H_0: p_A = p_B\) \(H_1: p_A < p_B\)\(p_A > p_B\)або\(p_A \ne p_B\) тест 6:2- PropzTest |
\(H_0: \mu_A = \mu_B\) \(H_1: \mu_A < \mu_B\)або\(\mu_A > \mu_B\) або\(\mu_A \ne \mu_B\) тест 4:2-SamptTest |
