11: Додаток А - Теорія лінійних хвиль
- Page ID
- 1697
У теорії для лінійних хвиль наведені рівняння для таких властивостей, як:
| швидкість частинок\((u, w)\) на будь-якій висоті в товщі води | \(m/s\) |
| прискорення частинок\((a_x, a_z)\) на будь-якій висоті в товщі води | \(m^2/s\) |
| зміщення частинок\((\xi , \zeta)\) на будь-якій висоті в товщі води | \(m\) |
| тиск (\(p\)) на будь-якій висоті в товщі води | \(N/m^2\) |
| швидкість хвилі (\(c\)) | \(m/s\) |
| швидкість групи хвиль\((c_g)\) | \(m/s\) |
| довжина хвилі\((L)\) | \(m\) |
| хвильовий профіль (\(\eta\)) | \(m\) |
| енергія хвилі на довжину хвилі на одиницю довжини гребеня\((E_t)\) | \(J/m\) |
| енергія на одиницю площі водної поверхні\((E)\) | \(J/m^2\) |
| потужність хвилі\((U)\) | \(J/m \times s\) |
Загальні рівняння цих властивостей можна знайти в таблиці А.2 стовпця «Перехідна глибина води». Рівняння перехідної глибини води містять гіперболічні функції. Може бути корисним використання стандартних таблиць, що містять значення гіперболічних функцій. Ці таблиці можна знайти в Посібнику з прибережної інженерії. Витяг з цих таблиць наведено в табл. А.3.
Таблиця A.1: Критерії глибоких і мілководних хвиль з похибкою порядку 1%

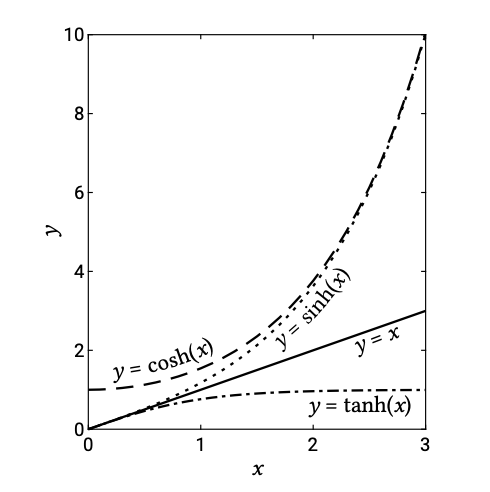
Для граничних випадків глибокого і мілководдя (див. Таблицю А.1) спрощення можна зробити в гіперболічних функціях (див. Також рис. A.1).
Для відносної глибокої води (\(h > L/2\)так\(kh > \pi\) де\(k = 2\pi /L\) знаходиться хвильове число):
\[\sinh kh = \dfrac{1}{2} (e^{kh} - e^{-kh}) = \dfrac{1}{2} e^{kh} \ \ \ \ \ \ \text{ for } kh \to \infty\]
\[\cosh kh = \dfrac{1}{2} (e^{kh} + e^{-kh}) = \dfrac{1}{2} e^{kh} \ \ \ \ \ \ \text{ for } kh \to \infty\]
\[\tanh kh = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ for } kh \to \infty\]
Для відносно мілководдя (\(h < L/20\)так\(kh < \pi /10\)):
\[\sinh kh = kh \ \ \ \ \ \ \ \text{ for } kh \to 0\]
\[\cosh kh = 1 \ \ \ \ \ \ \ \ \text{ for } kh \to 0\]
\[\tanh kh = kh \ \ \ \ \ \ \ \text{ for } kh \to 0\]
Таблиця А.2: Вирази для обчислень дрібних, перехідних і глибоководних хвиль відповідно до теорії лінійних хвиль. Зверніть увагу, що на відміну від визначень в главах 3 і 5,\(z = 0\) на дні (замість\(z = -h\)) і\(z = h\) на середньому рівні води (замість\(z = 0\)).

З рівнянь у таблиці А.2 в цих конспектах часто використовуються наступні:
\[\omega^2 = \left ( \dfrac{2\pi }{T} \right )^2 = gk \tanh kh \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ dispersion relation } [1/s^2]\]
\[k = \dfrac{2\pi}{L} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{wavenumber} [1/m]\]
\[n = \dfrac{c_g}{c} = 0.5 \left ( 1 + \dfrac{2kh}{\sinh 2kh} \right ) \ \ \ \ \ \ \ \ \ \ \ [-]\]
Таблиця A.3: Лінійні хвильові функції

Дисперсійна залежність неявна з точки зору хвильовогочисла. Це означає, що для вирішення рівняння для перехідної глибини води необхідний ітераційний процес (для обчислення\(L\) з заданого\(h\) і\(T\)). Існують також явні вирази, які наближають рішення близько. Крім того, використання може бути зроблено з таблиці перегляду, як Таблиця A.3, яка дає\(h/L\) для даного\(h/L_0\) (з глибокою довжиною хвилі води\(L_0 = gT^2/2\pi\)).

Зсув частинок води показано на рис. А.2 для хвилі на мілководді і для хвилі в глибокій воді. У глибокій воді хвильовий рух не поширюється вниз до русла; на мілководді вода здійснює коливальний рух по всій глибині. Біля поверхні частинки води описують еліптичний шлях; біля дна частинки води здійснюють горизонтальний коливальний рух.
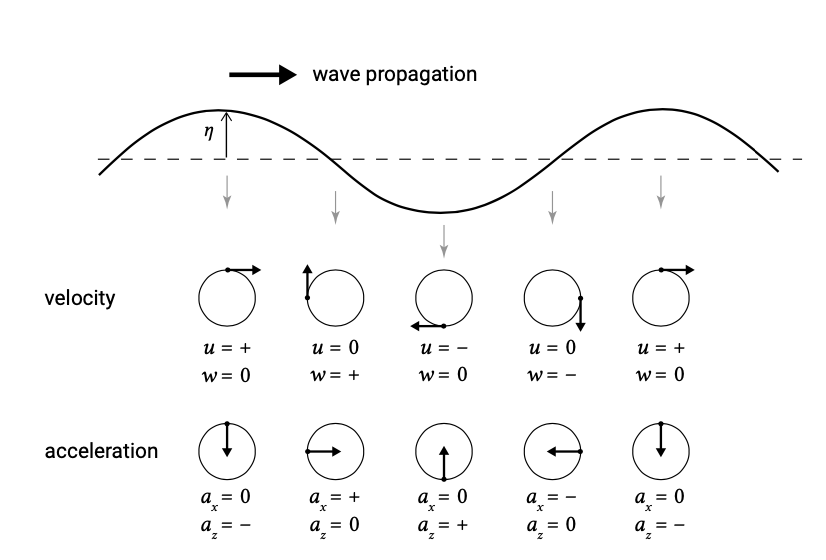
На малюнку А.3 показано співвідношення між напрямком швидкості і прискоренням частинок води на певних фазах в хвильовому періоді.
