6.2.3: Швидкість падіння

Малюнок 6.1: Сили на «сфері» у прозорій воді.

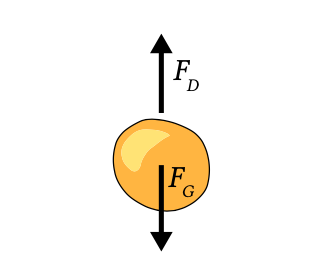
Коли частинка потрапляє в тиху і чисту воду, вона прискорюється, поки не досягне постійної вертикальної швидкості, яка називається швидкістю падіння або швидкістю осідання. Цю швидкість можна оцінити за балансом між спрямованою вниз силою тяжіння\(F_G\) (мінус ефект плавучості) і спрямованою вгору (уповільнює) силою опору,\(F_D\) як зазначено на рис. 6.1.

Основне рівняння

Спрямована вниз сила тяжіння\(F_G\) на сферу в поєднанні з ефектом висхідної плавучості задається так званим підводним вагою сфери, тобто вагою сфери за вирахуванням ваги зміщеного об'єму води. При вазі, рівній масі раз прискорення за рахунок сили тяжіння, ми маємо для ідеальної сфери:

\[F_G = (\rho_s - \rho) g \left (\dfrac{\pi}{6} D^3 \right )\]

де:

\(\rho_s\)	масова щільність частинки	\(kg/m^3\)
\(\rho\)	масова щільність навколишньої рідини	\(kg/m^3\)
\(D\)	діаметр частинок	\(m\)
\(g\)	прискорення гравітації	\(m/s^2\)

У цьому рівнянні термін між дужками - це обсяг сфери.

Спрямована вгору сила дорівнює так званій силі перетягування, що позначається:

\[F_D = \dfrac{1}{2} C_D \rho w_s^2 \left (\dfrac{\pi}{4} D^2 \right )\]

де:

\(C_D\)	коефіцієнт опору
\(w_s\)	швидкість падіння частинок	\(m/s\)

Другий термін між дужками відноситься до перетину сфери. Сила перетягування не дорівнює нулю, тільки якщо\(w_s > 0\).

У рівновазі обидві сили знаходяться в рівновазі, а швидкість падіння\(w_s\) (в\(m/s\)) задається:

\[w_s = \sqrt{\dfrac{4(s - 1) gD}{3C_D}}\label{eq6.2.3.3}\]

в\(s\) якому відносна щільність (див. 6.2.2).

Швидкість падіння частинки залежить від її розміру, щільності та величини коефіцієнта опору\(C_D\). Цей коефіцієнт опору залежить від форми частинки, її шорсткості, але в основному від числа Рейнольдса зерна:

\[\text{Re} = w_s D/v\]

де

\(v\)

кінематичний коефіцієнт в'язкості

\(m^2/s\)

Кінематична в'язкість визначається як динамічна в'язкість, поділена на щільність води:\(v = \mu /\rho\). Характерне значення для\(v\) є\(10^{-6}\ m^2/s\). Динамічна в'язкість представляє внутрішній опір рідини потоку («товщина») і є функцією температури і в меншій мірі щільності.

Залежність від числа Рейнольдса

Малюнок 6.2: Коефіцієнт опору як функція числа Рейнольдса (Vanoni, 1975).

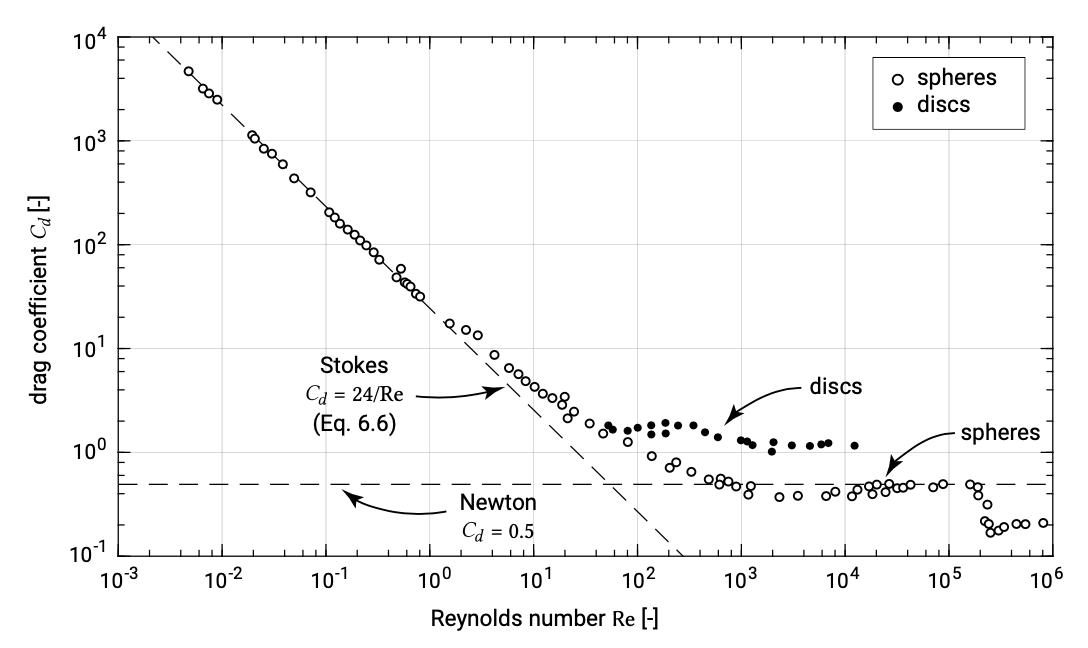
Для низькозернистих чисел Рейнольдса (\(\text{Re} < 0.1\)до 0,5) в так званому діапазоні Стокса коефіцієнт опору можна описати (див. Рис. 6.2):

\[C_D = 24/\text{Re}\]

врожайність:

\[w_s = \dfrac{(s - 1) gD^2}{18v}\]

У цьому діапазоні швидкість падіння залежить від квадрата діаметра зерна, відносної щільності і кінематичного коефіцієнта в'язкості.

Для високозернистих чисел Рейнольдса (\(400 < Re < 2 \times 10^5\)), в так званому діапазоні Ньютона, коефіцієнт опору стає постійним (\(C_D \approx 0.5\)). У такому випадку це випливає з Eq. \(\ref{eq6.2.3.3}\):

\[w_s = 1.6 \sqrt{gD(s - 1)}\]

У цьому діапазоні швидкість падіння залежить від квадратного кореня діаметра зерна і відносної щільності і не залежить від кінематичного коефіцієнта в'язкості. Це також стосується надзвичайно високих чисел Рейнольдса (\(\text{Re} > 2 \times 10^5\)), де коефіцієнт опору (постійний) близько 0,2.

Для кварцових сфер, що падають у негазованій воді, число Рейнольдса 0,5 приблизно відповідає діаметру частинок 0,08 мм, тоді як число Рейнольдса 400 відповідає діаметру близько 1,9 мм. Оскільки більшість пляжних відкладень падають в діапазоні від 0,08 мм до 1,9 мм, в більшості практичних випадків ні наближення Стокса, ні наближення Ньютона не можуть бути використані.

Малюнок 6.3: Швидкість падіння осаду в залежності від розміру зерна в прісній воді з температурою\(18^{\circ}\) (\(\rho_w = 1000\ kg/m^3, \rho_s = 2650\ kg/m^3\)і\(v = 1.05 \times 10^{-6}\ m^2/s\)). Порівняння між Ван Рейн (1984b) та Аренсом (2000).

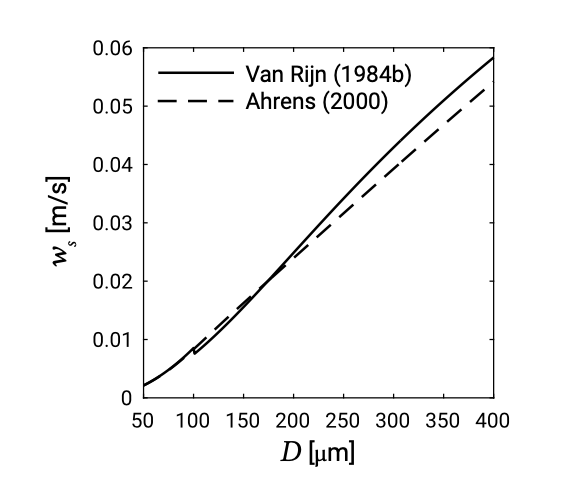
Для дуже дрібних частинок (мулу, глини) швидкість падіння пропорційна\(D^2\); для частинок гравію розмір пропорційна швидкості падіння\(\sqrt{D}\). Для піску швидкість падіння падає в перехідному діапазоні між\(D^2\) залежністю та\(\sqrt{D}\) залежністю. Через відсутність простого співвідношення коефіцієнта опору в цьому діапазоні прийнято використовувати емпіричні формули для швидкості падіння. У літературі можна знайти багато формул (наприклад, Ван Рейн (1984b) та Аренс (2000)). Як приклад, на рис. 6.3, для двох формул побудована швидкість падіння в залежності від діаметра зерен.

Утруднене заселення

У сумішах з високою концентрацією швидкість падіння однієї частинки знижується за рахунок присутності інших частинок. Це можна пояснити наступним чином: при кожному русі зерен вниз аналогічний обсяг рідини повинен витікати вгору; цей висхідний потік уповільнює інші зерна. Для того, щоб врахувати цей утруднений ефект осідання, швидкість падіння в суміші рідина-осад повинна визначатися як функція концентрації осаду\(c\) та швидкості падіння частинок\(w_s\). Часто використовувана рецептура для ефективної швидкості падіння в суміші є:

\[w_e = (1 - c)^{\alpha} w_s\]

де:

\(w_e\)	ефективна швидкість падіння	\(m/s\)
\(w_s\)	швидкість падіння одного зерна в прозорій воді в спокої	\(m/s\)
\(c\)	концентрація осаду (об'ємний%, об'єм частинок твердого осаду в об'ємі водно-осадової суміші)	-
\(\alpha\)	коефіцієнт (від 4.6 при низьких числах Рейнольдса до 2.3 при високих числах Рейнольдса)	-

У багатьох інженерних випадках, пов'язаних з транспортуванням осаду, концентрація осаду може становити приблизно до 1% (\(2.65\ kg/m^3\)), що означає, що вплив концентрації осаду на швидкість падіння невеликий. Це не так в умовах потоку аркушів (див. 6.4.2) і в дуже мулистих середовищах, де концентрації осаду можуть бути значно вищими.