Рішення
- Page ID
- 66878
Модуль 1 Теорія наборів
Набір вправ 1 Рішення
| а. 5П, 6П, 7П, 8П | ||||||
| б. 4Д, 5Д, 6Д, 7Д, 8Д, 9Д | ||||||
| c. 5H, 6H, 7H, 9H | ||||||
|
д. існує 6 груп. Ви повинні були перерахувати 2 з цих груп:
|
5. колекція предметів
6. об'єкти в наборі
7. Нульовий набір - це набір, який не містить елементів, тобто він порожній.
9. Так.
| N = {4Н, 5Н, 6Н, 7Н, 8Н} |
| Q = {4Q, 5Q, 6Q, 7Q, 8Q, 9Q} |
| S = {4Н, 4Д, 4Q} |
| Ш = {6П, 6Н, 6Д, 6Q, 6H} |
| Y = {8P, 8N, 8D, 8Q} |
| Т = {} |
10.
|
a. так; достатньо будь-якого елемента N 4Н, 5Н, 6Н, 7Н або 8Н |
б. немає | c. ні | d. так |
11. Відповіді можуть відрізнятися. Будь-якого елемента в Р вистачить 5P, 6P, 7P або 8P
12.
| а. ф | б. т | c. Т | д. Т | е. Ф |
| ф. Т | г. Т | ч. т | i. Ф |
| а. 4 | б. 5 | с. 6 | д. 6 | д. 3 | ф. 4 |
| г. 4 | ч. 0 | i. 3 | дж. 5 | к.5 | л. 5 |
| м. 25 | п. 0 | o Z ~ S; P ~ H, H ~ Y; N ~ W; X ~ V; Q ~ D (не обов'язково включати будь-які нульові підмножини) |
15.
| а. Ø | б. {9H} | c. {4H} |
| д. {6Q} | е. Ø |
17. Два множини, A і B, є нероз'єднаними\(A \cap B = Ø\), якщо це означає, що їх перетин порожній.
18. 5D, 6P, 7P, 8P, 5P, 5N, 5Q, 5H. так, Є 8 монет.
19.
| а. {4Н, 5Н, 6Н, 7Н, 8Н, 4Д, 4Q} |
| б. {4Q, 5Q, 6Q, 7Q, 8Q, 9Q, 6P, 6N, 6D, 6H} |
| c. {5П, 6П, 7П, 8П, 4Д, 5Д, 6Д, 7Д, 8Д, 9Д} |
| д. {7П, 7Н, 7Д, 7Q, 7Н, 8П, 8Н, 8Д, 8Q} |
23.
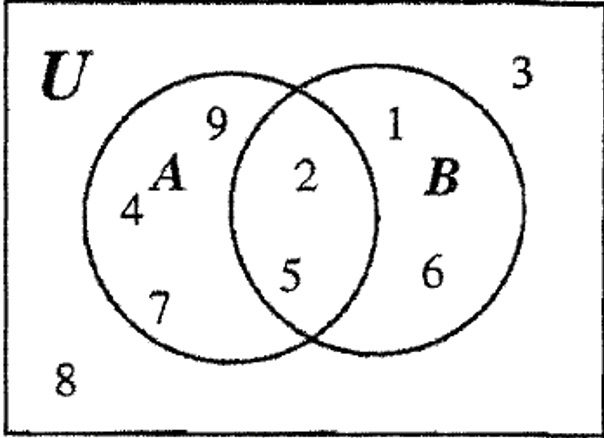
| a. {2, 4} | б. {3, 5} |
| c. {} або Ø | д. {1, 2, 3, 4, 5, 6, 8} |
| е. {1, 2, 3, 4, 5, 7} | f. {2, 3, 4, 5, 6, 7, 8} |
| г. {6, 7, 8, 9} | h. {1, 3, 5, 7, 9} |
| i. {1, 2, 4, 6, 8, 9} | р. {1, 3, 5, 7} |
| j. {1, 3, 5} | q. {3, 5, 6, 7, 8, 9} |
| к. {6, 8} | р. {2,3,4,5,7} |
| л. {1, 2, 4} | с. {2, 4} |
| м. {7} | т. {6, 8, 9} |
| п. б або {2,4,6,8} | у. {7, 9} |
| o. С або {3,5,7} | v. {1, 3, 5, 6, 7, 8, 9} |
| ш. {7, 9} | x. {3, 5, 6, 7, 8, 9} |
| й. т | з. т |
| аа. F | бб. F |
| куб.см. Т | дд. F |
| ee. Т | Ф.Ф. |
| гг. F | ч-ч. Т |
| II. Т | Джей. F |
25.
| а. {a, b, c,..., z} |
| б. {124, 126, 128,..., 698} |
| c. {101, 102, 103,..., 999} |
| d. {x|x - колишній президент США до 1995 року} |
| e. {Рейган, Буш, Клінтон} |
30.
| а. 3; 8; відповіді можуть відрізнятися |
| б. 4; 6; відповіді можуть відрізнятися |
| c. 2; 12; відповіді можуть відрізнятися |
| d. 12; 2; відповіді можуть відрізнятися |
| д. 8; 3; відповіді можуть відрізнятися |
| f. 6; 4; відповіді можуть відрізнятися |
31. е. союз
32.
| c. ні |
| d. так; LYC, LYQ, LYT |
| е. перетин; {LYC, LYQ, LYT} |
34.
| а. {} |
| б. {}, {P} |
| c. {}, {Г}, {F}, {F, G} |
| d. {}, {X}, {Y}, {Z}, {X, Y}, {X, Z}, {Y, Z}, {X, Y, Z} |
| е. {}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {1, 3, 4}, {2, 3, 4}, {1, 3, 4}, {1, 2, 2, 4} 3, 4} |
35.
| а. 1 | б. 2 | c. 4 | д. 8 |
| е. 16 | ф. 32 | г.\(2^{n}\) |
36. 35
37. 35
38. так
39.
| а. н.е. | б.\(b^{2}\) | c.\(c^{2}\) |
40. Однією з можливостей є нехай A = {m} і B = {n}. Тоді\(A \times B = {(m,n)}\) але\(B \times A = {(n,m)}\). Тому\(A \times B \nleq B \times A\) (обов'язково напишіть своє рішення)
41.
| а. {(3,2), (3,6), (4,2), (4,6)} |
| б. {(6,5), (7,5), (8,5), (9,5)} |
| c. {} |
| d. {(a, a)} |
| е. {(х, х), (х, у), (у, х), (у, у)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
| г. {(9,4), D), (9,4), {a, b, c}), (C, D), (C, {a, b, c})} |
| ч. {({5,6,7,8,9}, г), ({5,6,7,8,9}, {4,3})} |
Набір вправ 2 Рішення
















18-56: Відповіді на ці вправи - діаграми Венна в кінці набору вправ 2.
Набір вправ 3 Рішення
1. Відповіді можуть відрізнятися. Перекриття - це перетин. Всього налічується 8 регіонів.
2.
|
а.  |
б.  |
|
c.  |
д.  |
4.
|
а.  |
|
б.  |
|
c.  |
5. Деякі можливості: трикутник, коло, квадрат; великий, малий і будь-яке інше значення.
8.
|
а.  |
| б. СТО, СТ, СГТ, ЛГТ, SYC, LYT, SRC, СГК, ЛРТ, ЛГК, LRC, LYC |
| c. СТО, СТ, СГТ, ЛГТ, SYC, LYT, SRC, СГК, ЛРТ, ЛГК, LRC, LYC |
| d Елементи абсолютно однакові |
| е.\(B \cup Q)^{c} = B^{c} \cap Q^{c}\) |
9.
|
а.  |
| б. СТО, ЛРК, ЛРТ, SRQ |
| c. СТО, ЛРК, ЛРТ, SRQ |
| d Елементи абсолютно однакові. |
| е.\((R^{c} \cup C)^{c} = R \cap C^{c}\) |
10. Для частини a та b остаточні затінення такі ж, як показано на діаграмі Венна нижче. Рівняння, яке ви можете записати, таке:\((B \cup Q)^{c} = B^{c} \cap Q^{c}\)

11. Для частини a та b остаточні затінення такі ж, як показано на діаграмі Венна нижче. Рівняння, яке ви можете записати, таке:\((A \cap B)^{c} = A^{c} \cup B^{c}\)

12.
| а.\(R \cup S\) | б. (\(M^{c} \cup N^{c})^{c}\) | c.\(F^{c} \cap G\) | д.\((H \cap I^{c})^{c}\) | е.\(P \cup Q^{c}\) | ф.\((S^{c} \cup T)^{c}\) |
14. Надано лише доказ до 14.c.
|
\((B^{c} \cup C)^{c} = (({2, 4, 6, 8}}}^{c} \cup {3, 5, 7}^{c}\) =\({1, 3, 5, 7, 9} \cup {3, 5, 6})^{c}\) =\(({1, 3, 5, 7, 9})^{c}\) = {2, 4, 6, 8}. |
|
\(B \cap C^{c} = {2, 4, 6, 8} \cap ({1, 3, 5, 7, 9})^{c}\) =\({2, 4, 6, 8} \cap {2, 4, 6, 8}\) = {2, 4, 6, 8}. |
Так як\((B^{c} \cup C)^{c}\) і\(B \cap C^{C}\) мають точно такі ж елементи, вони рівні. Тому,\((B^{c} \cup C)^{c} = B \cap C^{c}\).
15.
|
a, b: остаточні затінення такі ж, як показано на діаграмі Венна нижче.  |
| c. {2,3,4,5} |
| д. {2,3,4,5} |
| е. вони однакові рівні. |
16.
|
a, b: остаточні затінення такі ж, як показано на діаграмі Венна нижче.  |
| c. {1,2,3,4,5} |
| д. {1,2,3,4,5} |
| е. вони однакові. |
17.
| а. (\(X \cap Y) \cup (X \cap Z\)) |
| б.\((P \cup Q^{c}) \cap (P \cup R\)) |
| c.\(K^{c} \cap (L \cup M)\) |
| г.\(D \cup (E^{c} \cap F\)) |
Набір вправ 4 Рішення
1.
2.
3.
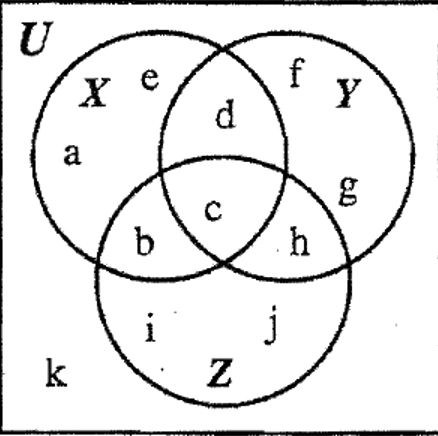
| а.\((A \cup B \cup C)^{c}\) | б. а - (\(B \cup C)\) |
| c. (А\ ковпачок B) - C | д. б - (\(A \cup C)\) |
| д.\((A \cap B \cap C\)) | ф.\((A \cap C) - B\) |
| г.\((B \cap C) - A\) | ч.\(C - \(A \cup B)\) |
4.
| а. 43 | б. 51 | c. 46 | д. 38 |
| д. 18 | ф. 25 | г. 13 | ч. 89 |
5.
| а. п (\(A - (B \cup C)\)) = 11 |
| б. п (А) = 69 |
| с. п (\(B \cap C\)) = 51 |
| д. п (\((A \cup B) - C\)) = 71 |
| е. п (\(C^{c}\)) = 73 |
| ф. п (\(B \cup C\)) = 160 |
| г. п (В - С) = 60 |
| ч. п (\((A \cap B) \cup (B \cap C) \cup (A \cap C)\)) = 66 |
| i. п (\((A \cap B) \cup (B \cap C) \cup (A \cap C) - (A \cap B \cap C)\)) = 23 |
6.
| а. 34 | б. 5 | c. 69 | д. 37 | д. 13 |
| ф. 3 | г. 21 | ч. 9 | я. 23 |
7.
|
а. 12  |
б. 2 | с. 6 |
8.
| а. 9 | б. 5 | c. 10 | д. 43 |
|
д. 37 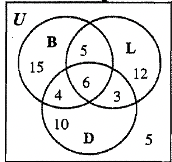 |
ф. 18 | г. 3 |
9.
| а. 86 | б. 49 | c. 31 |
| д. 25 | е. 4 | ф. 27 |

10. Це один із способів показати це.

11. Це один із способів показати це.

12. Це один із способів показати це.

Рішення для домашніх завдань
1.
| a. {a, c} |
| c. {e, v, w, z} |
| е. {r, u, x} |
| г. {a, c, r, u} |
| i. {x} |
| к. Ø або {} |
| м. 10 |
| п. 2 |
3. а.\((N^{c} \cap P)^{c}\)
4. а.\(A^{c} \cup (E \cap F\))
5.
|
а.  |
| с. 15 |
| е. 5 |
| г. 9 |
6.
| а. 8 | б. 3 |
7.
| а. т | c. F | е. Т |
8.
|
а.  |
c.  |
е.  |
9. а.\(A \cup (B \cap C)\)
10.
a. {}
c. {}, {a}, {b}, {a, b}
11.
| a. {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (4, 1), (4, 2), (4, 4)} |
| c. {({a, c}, {a, c}), ({a, c}, 5), (5, {a, c}), (5, 5)} |
| е. {(x, x)} |
12.
| a. {LBC, LYC, LGC} |
| c. {LRC, LBC, LGC, LYC, SRC} |
Модуль 2 Підрахунок і числівники
Набір вправ 1 Рішення
8. Набори мають однакову кількість елементів. Кардинальність дорівнює.
10.
|
а) 1)\(1 \leftrightarrow A\) |
|
б. 1)\(2 \leftrightarrow B, 3 \leftrightarrow C\) 2)\(2 \leftrightarrow C, 3 \leftrightarrow B\) |
|
c. 1)\(4 leftrightarrow D, 5 leftrightarrow E, 6 leftrightarrow F\) 2)\(4 leftrightarrow D, 5 leftrightarrow F, 6 leftrightarrow E\) 3)\(4 leftrightarrow E, 5 leftrightarrow D, 6 leftrightarrow F\) 4)\(4 leftrightarrow E, 5 leftrightarrow F, 6 leftrightarrow D\) 5)\(4 leftrightarrow F, 5 leftrightarrow D, 6 leftrightarrow E\) 6)\(4 leftrightarrow F, 5 leftrightarrow E, 6 leftrightarrow D\) |
11.
|
а) 1)\(M \leftrightarrow M\) |
|
б. 1)\(x \leftrightarrow x, y \leftrightarrow z\) 2)\(x \leftrightarrow z, y \leftrightarrow x\) |
|
c. 1)\(1 \leftrightarrow 1, 2 \leftrightarrow 2\) 2)\(1 \leftrightarrow 2, 2 \leftrightarrow 1\) |
|
д. 1)\(1 \leftrightarrow 1, 2 \leftrightarrow 2, 3 \leftrightarrow 3\) 2)\(1 \leftrightarrow 1, 2 \leftrightarrow 3, 3 \leftrightarrow 2\) 3)\(1 \leftrightarrow 2, 2 \leftrightarrow 1, 3 \leftrightarrow 3\) 4)\(1 \leftrightarrow 2, 2 \leftrightarrow 3, 3 \leftrightarrow 1\) 5)\(1 \leftrightarrow 3, 2 \leftrightarrow 1, 3 \leftrightarrow 2\) 6)\(1 \leftrightarrow 3, 2 \leftrightarrow 2, 3 \leftrightarrow 1\) |
|
е. 1)\(1 \leftrightarrow 3, 2 \leftrightarrow 4, 3 \leftrightarrow 5\) 2)\(1 \leftrightarrow 3, 2 \leftrightarrow 5, 3 \leftrightarrow 4\) 3)\(1 \leftrightarrow 4, 2 \leftrightarrow 3, 3 \leftrightarrow 5\) 4) 1\ стрілка вліво вправо 4, 2\ ліва стрілка вправо 5, 3\ стрілка вліво вправо 3 5) 1\ ліва стрілка вправо 5, 2\ ліва стрілка вправо 3, 3\ стрілка вліво вправо 4 6) 1\ ліва стрілка вправо 5, 2\ стрілка вліво вправо 4, 3\ стрілка вліво вправо 3 |
12.
| а. 1 | б. 2 | с. 6 |
14.
| а. | | | | | | | | | | |
| b. зробити 512 міток обведення; зробити 2 000 000 позначок обведення. |
16.
| а. | | | | | | | | | | | | | | | |
|
б.  |
17. 36
18. Відповіді можуть відрізнятися. Деякі можливості полягають в тому, щоб зробити 123 штрихи або зробити 8 I і 53 штрихів.
19.
| а. 301 020 | б. 4 010 507 |
| c. 35 000 | д. 110 023 |
20.
|
а.  |
|
б.  |
|
c.  |
|
д.  |
|
е. 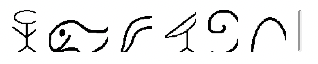 |
21. Базова десятка. Вони мають лише символи до мільйона в єгипетському. Це робить написання дуже великих числівників занадто громіздким і, можливо, практично неможливим.
24.
| а. XXXII | б. DLXI |
| c. позову 8 | д. ММЛІІІ |
25.
| а. 2 687 | б. 1 232 |
26.
| а.\(\bar{\text{CCCXXX}}\) DCCCII |
| б.\(\bar{\bar{\text{LXX}}}\) MDCLI |
27.
| а. CCCCCCCCXXXXIII або ДККХХХХХХІІІІІ |
| б. ХХХХХХХХХХХХХХІІІІІІІІІІІІІІІІ ККХХХХ |
29.
| а. ДКХХЛ ІІІ |
| б.\(\bar{\text{XIV}}\) CDLXXX |
| c. CMXXIX |
| д. CDXLII |
30.
| а.\(\bar{\text{XIX}}\) CDLIII |
| б. ММДКККХЛІКС |
| c. МКМХКВІ |
32. 3, 1, 3, 1, 3, 1
33.
| а. 10 | б. 1 | c. 2 |
| д. 7 | е. 7 |
34.
| а. 3 |
| б. 2 |
| c. 9 |
| д. 900 ударів |
| е. 180 5 розрядів розрядів |
35.
Індуї-Арабська: 3, 3, 7, 5, 4
Розряди: 143, 400, 1000000, 30009, 2124
Кількість: 31, 80, 200000, 6005, 428
Єгипетський: 8, 4, 1, 12, 9
Роман: 6, 2, 1, 5, 7
Набір вправ 2 Рішення
1.
|
а. 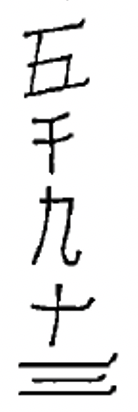 |
б.  |
c.  |
д. 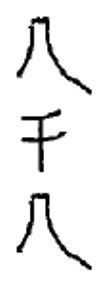 |
2.
| а. 109 | б. 6063 | c. 40 | д. 2815 | e.7800 |
3.
|
1.  |
5. 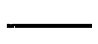 |
9.  |
13.  |
17. 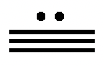 |
|
2.  |
6.  |
10.  |
14.  |
18.  |
|
3.  |
7.  |
11.  |
15.  |
|
|
4.  |
8.  |
12.  |
16.  |
19.  |
4. Крапка представляє номер один, а відрізок лінії - число п'ять. Будь-яка комбінація з 1-3 відрізків ліній і/або 1-4 крапки утворює будь-яку цифру до 19.
5.
| а. 90 | б. 320 | c. 162 |
6.
| а. 3974 | б. 1946 р. | с. 3300 |
| д. 32454 | д. 7319 |
7.
|
а.  |
б.  |
c.  |
д.  |
е.  |
8.
| а. 27 рем. 156 |
| б. 9 рем. 6709 |
| c. 16 рем. 13 |
| д. 2 рем. 142040 |
9. А 19 на другому рівні вгору дорівнює 380. Числівник майя для 380 наведено нижче.

10. Ви не можете мати вище 17 на другому рівні вгору, тому що 18 на цьому рівні представляють 360, які повинні бути представлені на третьому рівні вгору. Для всіх інших рівнів найвища цифра може бути 19.
11.
|
а.  |
б.  |
c. 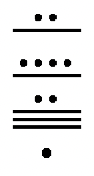
 |
д.  |
е. |
12.
|
а.  |
б.  |
c.  |
13.
| а. 10 | б. 12 | с. 3 |
14.
| китайська | Майя | |
| а. 15 |
 |
 |
| б. 100 |
 |
 |
| c. 1000 |
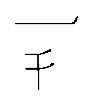 |
 |
| д. 9999 |
 |
 |
Набір вправ 3 Рішення
1.
| а. 2 | б. 2 | c. 2 | д. 2 | е. 2 |
2.
| а. 27 | б. 13, 1, 14 |
| с. 6, 1, 1, 8 | д. 3, 0, 1, 1, 5 |
| е. 1, 1, 0, 1, 1, 4 | ф. 1, 1, 0, 1, 1 |
| г. 27, 4 |
3.
| а. 18 | б. 9, 0, 9 |
| с. 4, 1, 0, 5 | д. 2, 0, 1, 0, 3 |
| е. 1, 0, 0, 1, 0, 2 | ф. 1, 0, 0, 1, 0 |
4.
| а. 45 | б. 22, 1, 23 |
| с. 11, 0, 1, 12 | д. 5, 1, 0, 1, 7 |
| е. 2, 1, 1, 0, 1, 5 | |
| ф. 1, 0, 1, 1, 0, 1, 4 | |
| г. 1, 0, 1, 1, 0, 1 |
5.
| a. три, нуль, два, шість базових |
| б. один, нуль, один, один, база два |
| c. чотири, три, п'ять, сім базових |
6.
| а.\(5016_{\text{eight}}\) | б.\(101001_{\text{two}}\) |
7.
| 2048, 1024, 512, 256,... |
8.
| а. 19 | б. 65 | c. 63 |
9. 3125, 625, 125, 25, 5, 1
10. 8
11. 2187, 729, 243, 81, 27, 9, 3, 1
12.
| а. 500 | б. 3711 | c. 1093 |
13.
| а. шість: 7776, 1296, 216, 36, 6, 1 |
| б. сімка: 16807, 2401, 343, 49, 7, 1 |
| c Дев'ять: 59049, 6561, 729, 81, 9, 1 |
| д. вісім: 32768, 4096, 512, 64, 8, 1 |
| е. чотири: 1024, 256, 64, 16, 4, 1 |
| f. десять: 100000,10000,1000,100,100,10,1 |
| г Дванадцять: 20736, 1728, 144, 12, 1 |
| год Одинадцять: 14641, 1331, 121, 11, 1 |
14. \(n^{10}, n^{9}, n^{8}, n^{6}, n^{5}, n^{4}, n^{2}, n^{1}\)
15.
| а.\(3 \times 815 + 6 \times 811 + 2 \times 87\) |
| б.\(3 \times 515 + 4 \times 510 + 2 \times 57\) |
| c.\(4 \times 1114 + 3 \times 1110 + 2 \times 110\) |
| д.\(1 \times 214 + 1 \times 211 + 1 \times 24\) |
16.
| а.\(9^{6}\) | б.\(9^{0}\) | c.\(9^{12}\) | д.\(9^{10}\) |
17.
| а.\(2401000300_{\text{five}}\) |
| б.\(30040001600_{\text{eight}}\) |
| c.\(7000804000_{\text{twelve}}\) |
| д.\(201010200_{\text{three}}\) |
18.
| а.\(6^{17}\) | б.\(9^{19}\) |
19. 3:0, 1, 2
20. 4:0, 1, 2, 3
21. 5:0, 1, 2, 3, 4
22. 6:0, 1, 2, 3, 4, 5
23. 8:0, 1, 2, 3, 4, 5, 6, 7
24. Ні, оскільки єдині цифри, які можуть зустрічатися в числівнику Base Seven - це 0, 1, 2, 3, 4, 5 та 6.
25.
| а. сім |
| б. найвищої бази немає, вона може зустрічатися в будь-якій базі вище шести. |
26. 11
27. 12
28. 13
29.
| а. 671 | б. 1291 | c. 1830 |
| д. 3496 | д. 1358 | ф. 2231 |
30.
| а. 6 | б. 12 | c. 20 | д. 30 |
| д. 42 | ф. 56 | г. 72 | ч. 90 |
| я. 132 | дж. 156 | к. 182 | л. 420 |
31. \(13201154320050146_{\text{eleven}}\)більше. Вправа 30 ілюструє, що якщо дві цифри мають однакові точні цифри, той, що має вищу базу, має більш високе значення, оскільки кожне місце значення коштує більше. Пояснення можуть відрізнятися.
32. \(4 \times 1213 + 10 \times 129 + 11 \times 123\)
33. \(600T000E0000W00_{\text{thirteen}}\)
Набір вправ 4 Рішення
1. Запитайте у друга, як твоє художнє твір.
2.
| а. 4, 4, 4, 4, 4, 4 |
| б. 4,16,64,256 |
| с. 5 |
| д. 36 |
3. 2, 2, 2, 2, 2
4. 3, 3, 3
5. 4, 4, 4
6.а.
|
я. 42 Іі. 21, 0 іі. 10, 1, 0 iv. 5, 0, 1, 0 т. 2, 1, 0, 1, 0 vi. 1, 0, 1, 0, 1, 0 vii. Див. Перший ряд частини d. |
| б. див. другий ряд частини d. |
| c. див. третій ряд частини d. |
|
д. 101010 База Дві 001120 База три 000222 База Чотири |
7.
| а.\(110100_{\text{two}}\) |
| б.\(1221_{\text{three}}\) |
| c.\(310_{\text{four}}\) |
8.
| а.\(3020_{\text{four}}\) |
| б.\(1212_{\text{seven}}\) |
| c.\(1011001_{\text{two}}\) |
| д.\(100210_{\text{three}}\) |
| е.\(1E8_{\text{thirteen}}\) |
9.
| а.\(12202_{\text{three}}\) |
| б.\(10E_{\text{twelve}}\) |
| c.\(10011011_{\text{two}}\) |
| д.\(1110_{\text{five}}\) |
10.
| а.\(T23T_{\text{eleven}}\) |
| б.\(625T_{\text{thirteen}}\) |
11.
| а.\(59T_{\text{twelve}}\) |
| б.\(1506_{\text{eight}}\) |
| c.\(2305_{\text{seven}}\) |
| д.\(1131_{\text{nine}}\) |
13. 10
14. Остання цифра попереднього числівника повинна бути 9, а остання цифра нового числівника - 0.
15. 99 999 999
16. 1 000 000 000
17. 3
18. Остання цифра попереднього числівника повинна бути 2, а остання цифра нового числівника - 0.
19. \(1000000_{\text{three}}\)
20. \(2222222_{\text{three}}\)
21.
| а.\(1202011_{\text{three}}\) |
| б.\(2220012_{\text{three}}\) |
| c.\(1010110_{\text{three}}\) |
| д.\(2100220_{\text{three}}\) |
| е.\(2121000_{\text{three}}\) |
22.
| а.\(1200101_{\text{three}}\) |
| б.\(1202220_{\text{three}}\) |
| c.\(2110012_{\text{three}}\) |
| д.\(2110022_{\text{three}}\) |
23. Цифра «3" не може бути в числівнику.
24. \(0_{\text{four}}, 1_{\text{four}}, 2_{\text{four}}, 3_{\text{four}}, 10_{\text{four}}, 11_{\text{four}}, 12_{\text{four}}, 13_{\text{four}}, 20_{\text{four}}, 21_{\text{four}}, 22_{\text{four}}, 23_{\text{four}}, 30_{\text{four}}, 31_{\text{four}}, 32_{\text{four}}, 33_{\text{four}}, 100_{\text{four}}, 101_{\text{four}}, 102_{\text{four}}, 103_{\text{four}}, 110_{\text{four}}, 111_{\text{four}}, 112_{\text{four}}, 113_{\text{four}}\)
25. 1, 10, 11, 10, 101, 10, 11, 1000, 1001, 1011, 100, 101, 110, 111, 10000, 1001, 10010, 1001, 1001, 1010, 1010
26. 75, 76, 77, 100, 101, 102, 103, 104
27.
| а.\(3026_{\text{eight}}, 3030_{\text{eight}}\) |
| б.\(1234_{\text{five}}, 1241_{\text{five}}\) |
| c.\(101011_{\text{two}}, 101101_{\text{two}}\) |
28.
| а.\(12221_{\text{three}}\), 160 |
| б.\(2405_{\text{eight}}\), 1285 |
| с.\(1310_{\text{three}}\), 205 |
Набір вправ 5 Рішення
1.
| а.\(\frac{1}{4}\) | б.\(\frac{1}{16}\) | c.\(\frac{1}{64}\) |
| д.\(\frac{1}{3}\) | е.\(\frac{1}{25}\) | ф.\(\frac{1}{8}\) |
2.
| а. 35\(\frac{1}{4}\) | б. 168\(\frac{7}{11}\) |
| с. 15\(\frac{1}{2}\) | д. 27\(\frac{1}{2}\) |
3.
| а. 27\(\frac{13}{36}\) | б. 45\(\frac{27}{64}\) |
| c. 90\(\frac{9}{49}\) | д. 7\(\frac{5}{8}\) |
| д. 26\(\frac{26}{27}\) | ф. 1475\(\frac{5}{72}\) |
4.
| а. двійковий: 00110101; десятковий: 53 |
| б. двійковий: 10011010; десятковий: 154 |
| с. двійковий: 01010100; десятковий: 84 |
| d. двійковий: 00000000; десятковий: 0 |
| е. двійковий: 11111111; десятковий: 255 |
5.
| а. двійковий: 00110101; шістнадцятковий: 35 |
| б. двійковий: 10011010; шістнадцятковий: 9A |
| с. двійковий: 01010100; шістнадцятковий: 54 |
| д. двійковий: 00000000; шістнадцятковий: 00 |
| е. двійковий: 11111111; шістнадцятковий: FF |
6.
| а. двійковий: 01011110; десятковий: 94 |
| б. двійковий: 11100101; десятковий: 229 |
| с. двійковий: 00111001; десятковий: 57 |
| д. двійковий: 00011111; десятковий: 31 |
| е. двійковий: 10011000; десятковий: 152 |
| f. двійковий: 00101010; десятковий: 42 |
| г. двійковий: 00000111; десятковий: 7 |
| h. Двійковий: 01000000; десятковий: 64 |
7.
| a. Я ЛЮБЛЮ МАТЕМАТИКУ! |
| б. ВИКЛАДАННЯ Є СКЛАДНИМ, АЛЕ КОРИСНИМ КАР'ЄРА! |
8.
|
а. шестигранник: 48, 45, 4С, 50, 21 Бінарні файли: 01001000,01000101, 01001100, 01010000, 00100001 |
|
б. шестигранник: 2,45,20,48,41,50,50,59,2E Бінарні файли: 01000010, 01000101,00100000,0100100000,01000001,01010000, 01010000, 01010000, 01011001, 00101110 |
| c Це буде залежати від вашого імені! |
9.
| a. двійковий:\(1001001_{\text{two}}\) hex:\(49_{\text{sixteen}}\) |
| б. двійковий:\(1111010_{\text{two}}\) hex:\(7A_{\text{sixteen}}\) |
| c. двійковий:\(110010_{\text{two}}\) hex:\(32_{\text{sixteen}}\) |
| д. двійковий:\(11111010_{\text{two}}\) шістнадцятковий:\(FA_{\text{sixteen}}\) |
| е. двійковий:\(1111101000_{\text{two}}\) шістнадцятковий:\(3E8_{\text{sixteen}}\) |
Рішення для домашніх завдань
1. б. Немає можливості узгодження, оскільки кардинальність двох наборів різна
2. Однією з можливостей є:\(1 \leftrightarrow 5, 2 \leftrightarrow 10, 3 \leftrightarrow 15, 4 \leftrightarrow 20\), і т.д. дати власну відповідь
3.
(1)\(SBC \leftrightarrow SRC, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRQ\)
(2)\(SBC\leftrightarrow SRC, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRT\)
(3)\(SBC \leftrightarrow SRT, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRQ\)
(4)\(SBC \leftrightarrow SRT, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRC\)
(5)\(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRC\)
(6)\(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRT\)
4.
| а. 16 |
| c. 1962 |
| д. 744 |
| ф. 3 031 020 |
| год. 50 703 |
| в. 1395 |
| к. 971 |
5.
| а. CCCXLII |
|
c.  |
|
е. 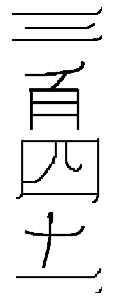 |
6.
| а.\(59T_{\text{twelve}}\) |
д. 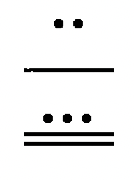 |
7. \(7T4E_{\text{twelve}}\)
10. а.\(17342575T_{\text{eleven}}\)
11. а.\(539100E0_{\text{twelve}}\)
13.
| а.\(10122_{\text{three}}\) | б. 98 |
14.
| а.\(300640000_{\text{seven}}\) | c.\(40T00E00_{\text{thirteen}}\) |
15.
| а.\(2 \times 911 + 5 \times 97 + 3 \times 94\) | c.\(8 \times 1210 + 11 \times 125 + 10 \times 123\) |
16.
| а.\(39\frac{1}{3}\) | б.\(16\frac{7}{9}\) |
18.
| а.\(302.301_{\text{four}}\) | c.\(101.1001_{\text{two}}\) |
Модуль 3 Додавання і віднімання
Набір вправ 1 Рішення
1.
| б. 3 | д. 4 | ф. 7 |
2.
| а. {t, u, v, w, x, y, z} | б. 7 | c. ні | д. ні | е. A & B не повинні мати спільних елементів. |
4.
| a. {ЛБТ, ЛБК, ЛБК, ЛРТ, ЛРК, ЛРК, ЛГТ, ЛГК, ЛГК, ЛГК, ЛГК, LYC, LYQ, SBT, СРТ, СГТ, СТ} | б. 16 | c. ні | д. л і Т мають спільні елементи. |
5.
|
а. нехай A = {x, y} і B = {a, b, c, d} 2+4 = п (А) + п (В) =\(n(A \cup B)\) = n ({x, y, a, b, c, d}) = 6 Тому 2 + 6 = 6 |
Оскільки n (A) = 2, n (B) =4, а\(A \cap B =Ø\), то підставивши n (A) на 2 і n (B) на 4 підставивши n (A) на 2 і n (B) на 4\(A \cup B\) шляхом обчислення підрахунком елементів в\(A \cup B\) |
|
б. нехай A = {x, y} і B = {a, b} 2+2 = п (А) +п (В) =\(n(A \cup B)\) = n ({x, y, a, b}) = 4 Тому 2 + 2 = 4 |
Оскільки n (A) = 2, n (B) =2, а\(A \cap B = Ø\), то підставивши n (A) на 2 і n (B) на 2 на множину теорії визначення складання\(A \cup B\) шляхом обчислення підрахунком елементів в\(A \cup B\) |
|
с. нехай A = {x, y, z} і B = {} 3 + 0 = п (А) + п (В) =\(n(A \cup B)\) = n ({x, y, z}) = 3 Тому 3 + 0 = 3 |
Оскільки n (A) = 3, n (B) =0, а\(A \cap B = Ø\), то підставивши n (A) на 3 і n (B) на 0 на множину теорії визначення складання\(A \cup B\) шляхом обчислення підрахунком елементів в\(A \cup B\) |
6.
| а. К | б. ч | в. б | д. о | е. с. |
| ф. п | г Б | ч. н | i. ч | Дж. б |
| к. н | л. ч | м. кожна пара дорівнює. |
8.
| а. у, Б | б. д, Б | c. те ж саме | д. Б, С | д., С | f. те ж саме |
11.
| а. комутативна властивість додавання |
| б. комутативне майно додавання |
| c. асоціативне властивість додавання |
| d. асоціативне властивість додавання |
13. Ш + Ш, Ш + Р, Р + Ш, Л
14. 1 + 1 + 1 = 3, 1 + 2 = 3, 2 + 1 = 3, 3 = 3
15. Р, Ш + Ш + Ш, Ш + Ш + Р, Ш + Р + Ш, Р + Ш + Ш, Ш + Л, Л + Ш, Р + Р
16. 4 = 4, 1 + 1 + 1 + 1 = 4, 1 + 3 = 4, 3 + 1 = 4, 2 + 2 = 4, 1 + 1 + 2 = 4, 1 + 2 = 4, 2 + 1 = 4, 2 + 1 + 1 = 4
17. Всього одинадцять поїздів: Р + П, Л+ Л, Р + Р + Р, Ш + Ш + Ш + Р, Ш + Ш + Ш + В, Ш + Ш + У, Ш + Ш + Ш + Ш + Ш + Ш + Ш + Р, Ш + Ш + Ш + Р, Ш + Ш + Р
18. 1 + 1 + 1 + 1 + 1 = 6, 1 + 5 = 6, 1 + 1 + 4 = 6, 1 + 1 + 1 + 2 = 6, 1 + 1 + 2 = 6, 1 + 1 + 1 + 3 = 6, 6 = 6, 2 + 2 + 2 = 6, 1 + 2 + 3 = 6, 1 + 2 + 3 = 6, 3 + 3 = 6, 3 + 3 = 6, 2 + 4 = 6
19.
| а. р | б. Y | c. N |
| д. р | е. П | ф. Вт |
20.
| б. тому що 30 = 22 + 8 |
| c. тому що 156 = 96 + 60 |
| д. тому що 80 = 0 + 80 |
| е. тому що 231 = 195 + 36 |
| f. тому що 987 = 967 + 20 |
21.
| б. тому що 30 + 69 = 99 |
| c. тому що 19 + 51 = 70 |
| д. тому що 0 + 32 = 32 |
| е. тому що 489 + 11 = 500 |
| f. тому що 65 + 136 = 201 |
22.
| а. ліворуч | б. право |
23. так
24. так
25.
| а. < | б. > |
26. {0, 1, 2, 3,.}
27. так
28. немає
29.
| а. закрито (починаючи з 0 + 0 = 0) |
| б. не закритий; 1 + 1 = 2 - контрприклад |
| c. закрито; мульт з 2: доказ залишається вам! |
| d. не закритий; 1 + 3 = 4 - контрприклад |
Набір вправ 2 Рішення
1.
|
а.  |
|
б.  |
|
c.  |
|
д.  |
2.
| а. б | б. д | с. г |
3.
| а. ДДДЦККККККААААА |
| б. ЕЕЕДКЦККБББ АААА |
| c. лют |
| д. е |
4.
|
а.  |
б.  |
c.  |
5.
|
а.  |
б.  |
c.  |
|
д.  |
е.  |
6. \(33_{\text{four}} + 31_{\text{four}} = 130_{\text{four}}\)
7. \(21_{\text{seven}} + 16_{\text{seven}} = 40_{\text{seven}}\)
8. \(1111_{\text{two} + 1101_{\text{two} = 11100_{\text{two}}\)
9. \(16_{\text{nine}} + 14_{\text{nine}} = 31_{\text{nine}}\)
10. \(120_{\text{three}} + 111_{\text{three}} = 1001_{\text{three}}\)
11. \(17_{\text{eight}} + 15_{\text{eight}} = 34_{\text{eight}}\)
13.
| а.\(2_{\text{nine}}\) | б.\(2_{\text{seven}}\) | c.\(T_{\text{twelve}}\) |
| д.\(8_{\text{eleven}}\) | е.\(4_{\text{six}}\) | ф.\(1_{\text{two}}\) |
| г.\(1_{\text{three}}\) | ч.\(3_{\text{four}}\) | я.\(2_{\text{five}}\) |
14.
| а.\(14_{\text{eleven}}\) | б.\(12_{\text{five}}\) |
| c.\(11_{\text{eight}}\) | д.\(11_{\text{thirteen}}\) |
| е.\(12_{\text{four}}\) | ф.\(13_{\text{seven}}\) |
| г.\(11_{\text{three}}\) | ч.\(10_{\text{two}}\) |
| я.\(12_{\text{six}}\) | Дж.\(13_{\text{nine}}\) |
15.
|
а. базова таблиця з трьома додаваннями  |
|
b. таблиця додавання шести базових  |
|
c Базова таблиця додавання двох 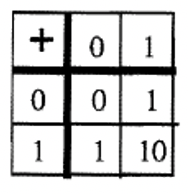 |
Набір вправ 3 Рішення
1.
| а. 50 | б. 51 | с. 47 | д. 52 |
2.
| а. 69 | б. 70 | c. 74 |
3.
| а. 47 | б. 43 | c. 53 | д. 53 |
4.
| а.\(1065_{\text{thirteen}}\) | б.\(10110_{\text{two}}\) |
| c.\(12222_{\text{five}}\) | д.\(1168_{\text{nine}}\) |
| е.\(110100_{\text{two}}\) | ф.\(10211_{\text{three}}\) |
| г.\(T450_{\text{twelve}}\) | ч.\(11521_{\text{seven}}\) |
6.
|
а. 43 + 47 = (40 + 3) + (40 + 7) = (40 + 40) + (3 + 7) = 80 + 10 = 90 |
|
б. 88 + 54 = (80 + 8) + (50 + 4) = (80 + 50) + (8 + 4) = 130 + 12 = 100 + 30 + 10 + 2 = 100 + 40 + 2 = 142 |
7. Перший учень додає ті (9 + 7 = 16), потім десятки (50 + 60 = 110) і по-третє, сотні (800 + 400 = 1200). Далі ці три проміжні суми складаються разом (16 + 110 + 1200 = 1326). Другий студент робить в основному те ж саме, за винятком сотень додаються спочатку, потім десятки і одиниці додаються. Перший студент додає справа наліво, тоді як другий студент додає зліва направо.
9.
| а. 12 109 | б. 111 463 |
| c. 16 668 | д. 128 334 |
10.
| а. 8 805 | б. 10 463 |
| c. 13 029 | д. 106 003 |
11.
| а.\(1300_{\text{six}}\) | б.\(1392_{\text{eleven}}\) |
| c.\(1166_{\text{eight}}\) | д.\(11001_{\text{two}}\) |
| е.\(3201_{\text{five}}\) | ф.\(1065_{\text{thirteen}}\) |
| г.\(10110_{\text{two}}\) | ч.\(12222_{\text{five}}\) |
| я.\(1168_{\text{nine}}\) | Дж.\(110100_{\text{two}}\) |
| к.\(10211_{\text{three}}\) | л.\(T450_{\text{twelve}}\) |
| м.\(11521_{\text{seven}}\) |
12.
| а. сім |
| б. тринадцять |
| с. дванадцять |
| д. три - тринадцять |
| е. чотири - тринадцять |
13.
| а. базова вісімка;\(132_{\text{eight}}\) |
| б. базова дев'ять:\(82_{\text{nine}}\) |
| с. основа три;\(110_{\text{three}}\) |
| d. базова десятка; 123 |
14. Вона вважала 68 як 70 - 2. Отже, 47 + (70 - 2) = (47 + 70) - 2 = 117 - 2 = 15
15. Спочатку він склав десятки разом, (40 + 60 = 100), потім склав їх разом (8 + 7 = 15) і, нарешті, він додав дві попередні суми разом (100 + 15 = 115).
18. 1115; РЕШІТКА ПОКАЗАНА НИЖЧЕ

19.
|
а.\(41_{\text{six}}\)  |
б.\(WOE_{\text{thirteen}}\)  |
20. Оцінка: $46; Фактична сума: $45.18
22. Ви будете недооцінювати, якщо вам трапиться округлити майже кожен елемент. Ви будете переоцінювати, якщо вам трапиться округлити майже на кожному пункті.
Набір вправ 4 Рішення
2.
| а. 7 | б. 3 | c. 4 |
4.
|
а. нехай A = {t, u, v, w, x, y, z} і B = {w, y, z}. Оскільки n (А) = 7, n (B) = 3 і\(B \subseteq A\), 7 - 3 = n (A) - n (B) шляхом підстановки n (A) на 7 і n (B) на 3 = n (A\ B) за визначенням теорії множин заміщення = n ({t, u, v, x}) шляхом обчислення A\ B = 4 шляхом підрахунку елементів в A\ B Тому 7 - 3 = 4. |
|
а. нехай A = {t, u, v, w, x, y, z} і B = {w, y, z}. Оскільки n (А) = 7, n (B) = 3 і\(B \subseteq A\), 7 - 3 = n (A) - n (B) шляхом підстановки n (A) на 7 і n (B) на 3 = n (A\ B) за визначенням теорії множин заміщення = n ({t, u, v, x}) шляхом обчислення A\ B = 4 шляхом підрахунку елементів в A\ B Тому 7 - 3 = 4. |
|
а. нехай A = {t, u, v, w, x, y, z} і B = {w, y, z}. Оскільки n (А) = 7, n (B) = 3 і\(B \subseteq A\), 7 - 3 = n (A) - n (B) шляхом підстановки n (A) на 7 і n (B) на 3 = n (A\ B) за визначенням теорії множин заміщення = n ({t, u, v, x}) шляхом обчислення A\ B = 4 шляхом підрахунку елементів в A\ B Тому 7 - 3 = 4. |
5.
|
а.  |
б.  |
6.

7.
|
а.  |
б.  |
|
c.  |
д.  |
8.
| \(32_{\text{five}}; 14_{\text{five}}; 13_{\text{five}}\) \(32_{\text{five}} – 14_{\text{five}} = 13_{\text{five}}\) |
9.
| \(21_{\text{eight}}; 7_{\text{eight}}; 12_{\text{eight}}\) \(21_{\text{eight}} – 7_{\text{eight}} = 12_{\text{eight}}\) |
10.
| \(210_{\text{three}}; 21_{\text{three}}; 112_{\text{three}}\) \(210_{\text{three}} – 21_{\text{three}} = 112_{\text{three}}\) |
12. Л
13.
| а. б | б. Y | c. N | д. н | е. с. |
14. Це робиться за допомогою C-Strips.
15. Ні; 7 —10 не є цілим числом
16.
| a. закрито | b. не закритий; 2-4 - контрприклад |
17.
| а. 12 - 4 = 8; 12 - 8 = 4 |
| б. 170 — 130 = 40; 170 — 40 = 130 |
| в. 80 - 62 = 18; 80 - 18 = 62 |
18.
| а. 4 = 7 —3 | б. 8 = 9 —1 |
19. № 4 < 7, але це не правда, що 7 < 4
21.
| а. 2; 9 = 7 + 2 | б. 7; 13 = 6 + 7 |
| в. 80; 88 = 8 + 80 | д. 56; 70 = 14 + 56 |
22. \(41_{\text{five}}\)
23. \(1_{\text{two}}\)
24. \(4E_{\text{twelve}}\)
25.
| а. -5 | б. 3 |
26.
|
а. 6 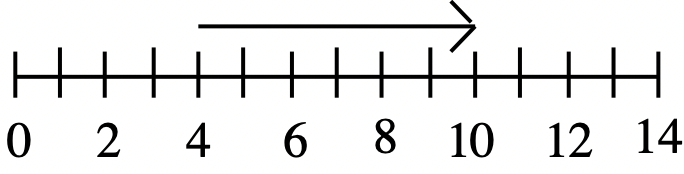 |
|
б. 7 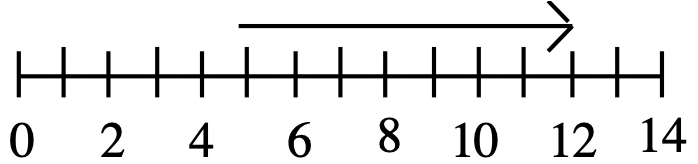 |
|
с. 5  |
|
д. 2 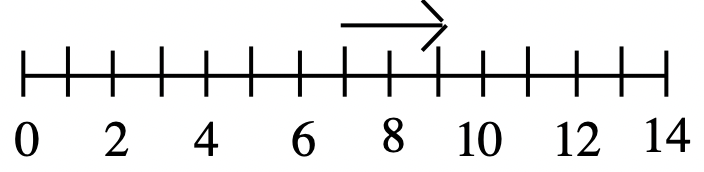 |
|
е. -7  |
|
ф. -3  |
|
г. -12 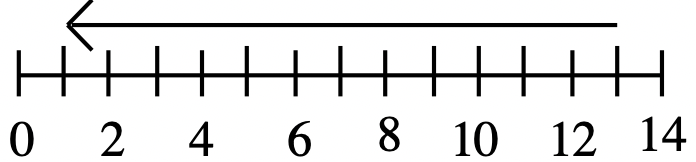 |
|
ч. 0  |
27. Вектор a: 6; вектор c: -5; вектор d: 3
Набір вправ 5 Рішення
1.
| а.\(314_{\text{thirteen}}\) | б.\(151_{\text{nine}}\) |
| c.\(1225_{\text{six}}\) | д.\(134_{\text{five}}\) |
| е.\(12_{\text{three}}\) |
2.
| в. 1618 | б.\(31_{\text{four}}\) |
| c.\(363_{\text{twelve}}\) | д.\(45_{\text{six}}\) |
| е.\(111_{\text{two}}\) | ф.\(254_{\text{nine}}\) |
| г.\(33_{\text{five}}\) | ч.\(234_{\text{seven}}\) |
| я.\(2_{\text{three}}\) | j.\(236_{\text{eight}}\) |
3. Покажіть чек, додавши відповідь до відніманого і переконавшись, що сума є мінуендом.
4.
| а. 6717 | б.\(1214_{\text{five}}\) |
| c.\(1424_{\text{eight}}\) | д.\(49E_{\text{thirteen}}\) |
| е.\(1010_{\text{two}}\) |
5. Покажіть чек, додавши різницю (відповідь) до відніманого і переконавшись, що сума є мінуендом.
6.
| а. 6697 | б.\(1144_{\text{five}}\) |
| c.\(1774_{\text{eight}}\) | д.\(4WE_{\text{thirteen}}\) |
| е.\(111_{\text{two}}\) |
7. Покажіть чек, додавши різницю (відповідь) до відніманого і переконавшись, що сума є мінуендом.
10.
| а. 9462 | б.\(122_{\text{four}}\) | c.\(101_{\text{two}}\) |
11. \(1_{\text{two}}\)
12.
| а. 4677 | б.\(134_{\text{five}}\) |
13.
| а Оскільки minuend є\(120_{\text{three}}\), наступний блок значення місця є базовим трьома блоками. Оскільки віднімання є\(12_{\text{three}}\), ми повинні розібратися, що додати,\(12_{\text{three}}\) щоб зробити блок. \(12_{\text{three}}\)є довгим і двома одиницями, тому я повинен додати 1 одиницю, 1 довгу і 2 квартири, щоб зробити блок. Тому, як 2 квартири, довгий блок до minuend\(120_{\text{three}}\), який дає 1 блок, 1 квартиру і 1 одиницю для нового minuend. Якщо я видалю найбільший блок з цього нового minuend, я повинен мати відповідь 1 квартира і 1 одиниця\(101_{\text{three}}\). Я залишив вам креслення. Дивіться #13 нижче, щоб дізнатися, як розпочати проблему зі скороченим малюнком. |
|
b Оскільки minuend є\(213_{\text{four}}\), наступним блоком значення місця є базовий чотири блок. Оскільки віднімання є\(133_{\text{four}}\), ми повинні розібратися, що додати,\(133_{\text{four}}\) щоб зробити блок. \(133_{\text{four}}\)це квартира, 3 лонги і три одиниці, так що я повинен додати 1 блок і 2 квартири, щоб зробити блок. Тому додайте 2 квартири та одиницю до minuend\(213_{\text{four}}\), що дає 1 блок і 2 лонги для нового minuend. Якщо я видалю найбільший блок з цього нового minuend, я повинен мати відповідь 2 лонгів. Отже, відповідь є\(20_{\text{four}}\). Ви можете використовувати скорочення для малюнка і почати з представлення кожного вихідного номера, як показано нижче. Я залишив частину, щоб додати і остаточне віднімання для вас  |
14.
| а. вона розбиває віднімання на три частини (100 + 50 + 2), віднімаючи за один раз значення місця. 634 — 100 = 534; 534 — 50 = 484; 484 — 2 =482. |
| б. він використовує комплементарний метод. Якщо додати 48 до 152, то вийде 200. Так він додає 48 до минуенду (634 + 48 = 682), а потім віднімає 200. |
Рішення для домашніх завдань
1. Надайте власні набори. Ось одне рішення.
а. по-перше, ми повинні визначити дві множини, A і B, які не з'єднані між собою, таким чином, що один набір має 5 елементів, а інший має 3 елементи.
Нехай A = {1, 2, 3, 4, 5} і B = {x, y, z}. Оскільки n (A) = 5, n (B) = 3 і\(A \cap B = Ø\), ми можемо знайти суму 5 і 3, спочатку сформувавши об'єднання A і B, а потім підрахувавши кількість елементів в їх об'єднанні. \(A \cup B\)= {1, 2, 3, 4, 5, x, y, z}. Оскільки n (\(A \cup B\)) = 8, то 5 + 3 = 8.
2. а. з 79 = 66 + 13
3. а. закритий під обидві операції
4.
|
а.  |
|
c.  |
5.
|
а.  |
|
c.  |
6.
| а.\(12325_{\text{six}}\) | б.\(2535_{\text{five}}\) |
13. а. 6

14.
| а. база 9 |
| c Основи від трьох до тринадцяти |
Модуль 4 Множення
Набір вправ 1 Рішення
1.
|
б. крок 1:  |
Крок 2:  |
c. крок 3:  |
d. обидва поїзда мають однакову довжину |
2.
| а. 2 темно-зелених | б. 6 червоних | с. 12, 12 | d. однакова довжина | е.\(R \times D = D \times R ; 2 \times 6 = 6 \times 2\) |
3.
| а. 7 світло-зелений | б. 3 чорні | с. 21, 21 | d. однакова довжина | е.\(K \times L = L \times K ; 7 \times 3 = 3 \times 7\) |
4.
| а. 12 білих | б. 1 яскраво-рожевий | с. 12, 12 | d. однакова довжина | е.\(H \times W = W \times H ; 12 \times 1 = 1 \times 12\) |
5.
| а. д | б. ш | c. р | д. п | е. л | ф. К | г. л | ч. р | i. р |
6.
|
a Це чотири поїзди, але вони, можливо, були перераховані в іншому порядку.  |
|
б. використовуючи поїзди, як зазначено вище, Поїзд 1:\(R \times D = H\), або\(2 \times 6 = 12\) Поїзд 2:\(P \times L = H\), або\(4 \times 3 = 12\) Поїзд 3:\(D \times R = H\), або\(6 \times 2 = 12\) Поїзд 4:\(H \times W = H\), або\(12 \times 1 = 12\) |
7. Червоний, R
8.
| а. 3 + 3 + 3 + 3 + 3 + 3 = 18 |
| б. 9 + 9 = 18 |
| c. 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 |
9.
| а.\(4 \times 3 = 3 + 3 + 3 + 3 = 6 + 3 + 3 = 9 + 3 = 12 ; 3 \times 4 = 4 + 4 + 4 = 8 + 4 = 12\) |
| б.\(2_{\text{five}} \times 3_{\text{five}} = 3_{\text{five}} + 3_{\text{five}} = 11_{\text{five}} ; 3_{\text{five}} \times 2_{\text{five}} = 2_{\text{five}} + 2_{\text{five}} + 2_{\text{five}} = 11_{\text{five}}\) |
10. Показані лише відповідь, а не окремі кроки
|
а.  |
|
б.  |
|
c.  |
11.
|
б.  |
с. 6 |
|
е.  |
ф. 6 |
| г. однакова довжина | ч. (\(R \times L ) \times P) = R \times (L \times P)\) |
| я.\((2 \cdots 3) \cdots 4 = 2 \cdots (3 \cdots 4)\) | j.\((2 \cdots 3) \cdots 4 = 6 \cdots 4 = 24; 2 \cdots (3 \cdots 4) = 2 \cdots 12 = 24\) |
| к. так |
12.
|
б.  |
c. 10 |
|
е.  |
ф. 10 |
| г. однакова довжина | ч.\((Y \times R ) \times L) = Y \times (R \times L)\) |
| я.\((5 \cdots 2) \cdots 3 = 5 \cdots (2 \cdots 3)\) | j.\((5 \cdots 2) \cdots 3 = 10 \cdots 3 = 30; 5 \cdots (2 \cdots 3) = 5 \cdots 6 = 30\) |
| к. так |
13. Виконайте порядок операцій, щоб спростити кожну сторону кожного рівняння в a - d.
14. Існують різні комбінації, які ви могли б використовувати для частини а.
15.
| а. 3 фіолетові смужки і 3 жовті смужки. | б. так само, як частина a |
| c.\(L \times (P + Y) = (L \times P) + (L \times Y)\) | д.\(4 \times (2 + 3) = (4 \times 2) + (4 \times 3)\) |
| е.\(4 \times (2 + 3) = 4 \times 5 = 20\) і\((4 \times 2) + (4 \times 3) = 8 + 12 = 20\) |
16.
| а. 2 білі смужки і 2 темно-зелені смужки | б. так само, як частина a |
| c.\(R \times (W + D) = (R \times W) + (R \times D)\) | д.\(2 \times (1 + 6) = (2 \times 1) + (2 \times 6)\) |
| е.\(2 \times (1 + 6) = 2 \times 7 = 14\) і\((2 \times 1) + (2 \times 6) = 2 + 12 = 14\) |
17. Виконайте порядок операцій, щоб спростити кожну сторону кожного рівняння в a - d.
18. Існують різні комбінації, які ви могли б використовувати для частини a і b.
19.
| а. р;\(1 \cdots 2 = 2\) | б. б;\(1 \cdots 9 = 9\) | в. д;\(1 \cdots 6 = 6\) |
| д. с;\(1 \cdots 11 = 11\) | е. н;\(8 \cdots 1 = 8\) | ф. ч;\(12 \cdots 1 = 12\) |
20. Ш, Ш
21.
| а.\(764 \cdots (1000 - 1) = 764 \cdots 1000 - 764 \cdots 1 = 764000 - 764 = 763236\) |
| б.\(324 \cdots (100 + 2) = 324 \cdots 100 + 324 \cdots 2 = 32400 + 648 = 33048\) |
| c.\(83 \cdots (74 + 26) = 83 \cdots 100 = 8300\) |
22. Переконайтеся, що ви знаєте всі властивості і можете надати приклади.
23.
| а. {(3,2), (3,6), (4,2), (4,6)} |
| б. {(6,5), (7,5), (8,5), (9,5)} |
| c. {} |
| d. {(a, a)} |
| е. {(х, х), (х, у), (у, х), (у, у)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
24. а. можуть бути використані будь-які два набори, один з яких має 5 елементів і один з 2 елементів. Це лише одне з можливих рішень. Нехай M = {a, b, c, d, e} і нехай N = {x, y}. Так як n (M) = 5 і n (N) = 2, то\(5 \times 2 = n(M \times N) = n({(a,x), (a,y), (b,x), (b,y), (c,x), (c,y), (d,x), (d,y), (e,x), (e,y)}) = 10\).
25.
| а.\(8 \times 6\) | б.\(3 \times 10\) | c.\(8 \times 6\) | д.\(5 \times 5\) | е.\(4 \times 14\) | ф.\(3 \times 7\) |
28. с.\(6 \times 4\)
30.
|
а.  |
б.  |
c.  |
д.  |
е. да |
31. Розподільна властивість множення над додаванням.
32. Робити це потрібно як вправа 30. Поясніть кроки, а також покажіть фотографії.
33.
| а. 8 | б. 8 | c. однакова довжина |
Набір вправ 2 Рішення
2.
|
\(13\ раз (29\) 1 —> 29 2 —> 58 4 —>116 8 —>232 — 232 + 116 + 29 = 377 |
\(29\ раз 13\) 1 —>13 2 —>26 4 —>52 8 —>104 16 —>208 — 208 + 104 + 52 + 13 = 377 |
3.
|
\(27\ раз 14\) 1 —> 14 2 —> 28 4 —> 56 8 —> 112 16 —> 224 — 224 + 112 + 28 + 14 = 378 |
\(14\ раз (27\) 1 —> 27 2 —>54 4 —>108 8 —>216 — 216 + 108 + 54 = 378 |
4.

5.
|
а. відповідь: 3,591  |
б. відповідь: 29,070  |
е. відповідь: 3,886 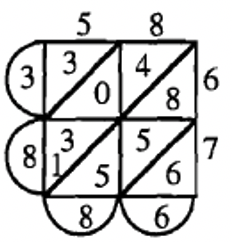 |
ф.  |
6.
| а.\(221_{\text{four}}\) |
б.  |
| c.\(1102_{\text{four}}\) | д.\(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
7.
| а.\(221_{\text{four}}\) |
б.  |
| c.\(1102_{\text{four}}\) | д.\(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
8. Зробіть дві палі підстави з трьох блоків, кожен з яких має 2 квартири, 2 лонги і одиницю. Дві рівні палі показані нижче.


Потім об'єднайте палі разом і зробіть відповідні обміни. Після здійснення обмінів, ось як це виглядає:

Напишіть основу три цифри, представлені після здійснення всіх обмінів. Відповідь є\(1212_{\text{three}}\).
9. Зробіть три палі підстави з трьох блоків, кожен з яких має 2 квартири, 2 лонги і одиницю. Три рівні палі показані нижче.

Потім об'єднайте палі разом і зробіть відповідні обміни. Після здійснення обмінів, ось як це виглядає:

Напишіть основу три цифри, представлені після здійснення всіх обмінів. Відповідь є\(2210_{\text{three}}\).
10.
| а. квартира | б. квартира | c. квартира | d.\(L \times L\) = F |
11.
| a. блок | a. блок | a. блок | д.\(F \times L\) = Б |
12.
| a. довгий блок | a. довгий блок | a. довгий блок | d.\(B \times L\) = ЛБ |
13.
| а. ф | б. Б | c. фунт | д. Б | е. ЛБ |
15.
| а. 3, 1 і 2 | б. 3 блоки, 1 квартира і 2 лонги |
16. Тут наведені тільки відповіді. Переконайтеся, що ви показуєте його з блоками та ПОЯСНІТЬ.
| а.\(1032_{\text{four}}\) | б.\(10122_{\text{three}}\) |
17.
| a. довгий блок | b. довгий блок | c. довгий блок | d.\(F \times F\) = ЛБ |
18.
| а. у | б. л | c. F | д. Б |
| е. л | ф. Ф | г Б | ч. F |
| i. Б | Дж.ЛБ |
20. Відповідь є\(20010_{\text{three}}\). Переконайтеся, що ви показуєте його з блоками та ПОЯСНІТЬ.
21. Вся таблиця показана:

22.
|
а.\(23_{\text{five}} \times 32_{\text{five}}\) = (2Л + 3У)\(\times\) (3Л + 2У) =\(2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U\) = 6Ф + 4Л + 9Л + 6У = 6Ф + 13Л + 6У = 1Б + 1Ф + 2Ф + 3Л + 1Л + 1У = 1Б + 3Ф + 4Л + 1У =\(1341_{\text{five}}\) |
|
\(42_{text{eight}} \times 53_{\text{eight}}\) = (4Л + 2У)\(\times\) (5Л + 3У) =\(4L \times 5L + 4L \times 3U + 2U \times 5L + 2U \times 3U\) = 20Ф + 12Л + 10Л + 6У = 20Ф + 22Л + 6У = 2Б + 4Ф + 2Ф + 6Л + 6У = 2Б + 6Ф + 6Л + 6У =\(2666_{\text{eight}}\) |
23.
\(212_{\text{four}} \times 102_{\text{four}}\)
= (2Ф + 1Л + 2У)\(\times\) (1Ф + 2У)
=\(2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U\)
= 2ФУНТ + 4Ф + 1Б + 2Л + 2Ф + 4У
= 2ФУНТ+1Б + 6Ф + 2Л + 4У
= 2ФУНТ+ 1Б + 1Б + 2Ф + 2Л + 1 Л
= 2ФУНТ+ 2Б + 2Ф + 3Л
=\(22230_{\text{four}}\)
24.
|
а.\(361_{\text{nine}} \times 15_{\text{nine}}\) = (3Ф + 6Л + 1У)\(\times\) (1Л + 5У) =\(3F \times 1L + 3F \times 5U + 6L \times 1L + 6L \times 5U + 1U \times 1L + 1U \times 5U\) = 3Б + 15Ф + 6Ф + 30Л + 1Л + 5У = 3Б +21Ф +31Л +5У = 3Б + 2Б + 3Ф + 3Ф + 4Л + 5У = 5Б + 6Ф + 4Л + 5У =\(5645_{\text{nine}}\) |
|
б.\(111_{\text{two}} \times 11_{\text{two}}\) = (1Ф+ 1Л + 1У)\(\times\) (1Л + 1У) =\(1F \times 1L + 1F \times 1U + 1L \times 1L + 1L \times 1U + 1U \times 1L + 1U \times 1U\) = 1Б + 1Ф + 1Ф + 1Л + 1Л + 1У = 1Б + 2Ф + 2Л + 1У = 1Б + 1Б + 1Ф + 1У = 1ФУНТ+1Ф + 1У =\(10101_{\text{two}}\) |
25.
|
a. відповідь:\(1422_{\text{six}}\)  |
б. відповідь:\(1469_{\text{eleven}}\)  |
c.\(100011_{\text{two}}\) |
| д.\(T09_{\text{twelve}}\) | е.\(20211_{\text{three}}\) | ф.\(2122_{\text{four}}\) |
26. Тут показані тільки a, b і c. Переконайтеся, що ви робите д і е.
 |
 |
 |
27.
| а.\(1103_{\text{five}}\) | б.\(1T58_{\text{thirteen}}\) | c.\(1022_{\text{three}}\) |
| д.\(16015_{\text{seven}}\) | е.\(16015_{\text{seven}}\) | ф.\(101310_{\text{four}}\) |
29. \(2144_{\text{five}}\)
30. \(31653_{\text{seven}}\)
31. \(10001111_{\text{two}}\)
32. \(1220212_{\text{three}}\)
33. \(15417_{\text{twelve}}\)
34. \(115503_{\text{six}}\)
35. \(2012220_{\text{three}}\)
36. \(424204_{\text{six}}\)
37. \(101001010_{\text{two}}\)
38. \(T73E8_{\text{twelve}}\)
39. \(615032_{\text{eight}}\)
40. \(1033230_{\text{four}}\)
41. \(2321411_{\text{five}}\)
42. \(1563526_{\text{seven}}\)
43. \(414025_{\text{nine}}\)
44. \(8T6697_{\text{eleven}}\)
Рішення для домашніх завдань
1. а. 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
3. а. п;\(4 \cdots 1 = 4\)
4. а. {(3,0), (3,1), (3,6), (х,0), (х,0), (х,6)}
6.
| а. б | c. фунт | е. ФБ |
10.
а. асоціативна властивість множення
Проілюструвати це рівняння вірно:\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Ліва сторона:\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 11_{\text{five}} \cdots 4_{\text{five}} = 44_{\text{five}}\)
Права сторона:\(2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}) = 2_{\text{five}} \cdots 22_{\text{five}}) = 44_{\text{five}}\)
Обидва вирази рівні\(44_{\text{five}}\), так\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Розподільна властивість множення додавання:
Проілюструвати це рівняння вірно:\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five)}}\)
Ліва сторона:\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = 2_{\text{five}} \cdots (12_{\text{five}}) = 24_{\text{five}}\)
Права сторона:\((2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}) = 11_{\text{five}} + 13_{\trxt{five}} = 24_{\text{five}}\)
Обидва вирази рівні\(24_{\text{five}}\), так\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}\))
Модуль 5 Двійкові операції
Набір вправ 1 Рішення
2.
| а. 16 | б. 65 | c. 2 | д. 42 | е. 4 |
| ф. 18 | г. 14 | ч. 41 | я. 20 |
3.
| а. м! п = п! м; Так; Доказ: Якщо м! п = п! м, тоді! є комутативним. м! n = 2 і n! м = 2. Так як обидва вирази (m! п і п! м) дорівнює 2, то! є комутативним. |
| б.\(m \bigoplus n = n \bigoplus m\); Так; Доказ: Якщо\(m \bogoplus n = n \bigoplus m\), то\(\bigoplus\) є комутативним. \(m \bigoplus n = 3mn\)і\(n \bigoplus m = 3nm\). Оскільки 3mn = 3nm, то\(m \bigoplus n = n \bigoplus m.\) отже, є комутативним. |
| c. m # n = n # m; Так; Надайте свій власний приклад з використанням чисел. |
| d. м n = n m; Так; Доказ: Якщо m n = n m, то є комутативним. м n = 2м + 2n, а n м = 2n + 2м. Так як 2м + 2n = 2n + 2м, то m n = n м. отже, є комутативним. |
| д.\(m \XBox n = n \XBox m\); Ні; Надайте свій власний лічильник, наприклад, використовуючи цифри. |
| f. m, n = n, m; Так; Доказ: Якщо m, n = n, m, то, є комутативним. \(m , n = m^{2} + n^{2}\)і\(n , m = n^{2} + m^{2}\). Так як\(m^{2} + n^{2} = n^{2} + m^{2}\), то m, n = n, m. отже, є комутативним. |
| g. m * n = n * m; Ні; Надайте свій власний контрприклад з використанням чисел. |
| h. m |
4.
| а. 17 | б. 4 | c. 2 | д. 216 | д. 36 | ф. 125 |
5.
| а. 270 | б. 34 | с. 27 | д. 6 | е. 6 |
| ф. 629 | г. 6 | ч. 4 | я. 12 |
6.
| а. (а! б) q c = а! (б! в); так; Доказ: Якщо (а! б)! с = а! (б! в), тоді! асоціативний. (а! б)! с = 2! c = 2, а а! (б! в) = а! 2 = 2. Так як обидва (а! б)! с і а! (б! в) дорівнюють 2, то! асоціативний. |
| б.\((a \bigoplus b) \bigoplus c = a \bigoplus (b \bioplus c)\); так; Доказ: Якщо\((a \bigoplus b)r c = a \bigoplus (b \bigoplus c)\),\(\bigoplus\) то асоціативний. \((a \bigoplus b) \bigoplus c = 3ab \bigoplus c = 3 \cdots 3ab \cdots c = 9abc,\)і\(a \bigoplus (b \bigoplus c) = a \bigoplus 3bc = 3 \cdots a \cdots 3bc = 9abc\). Так як обидва вирази\([(a \bigoplus b) \bigoplus c\) і\(a \bigoplus (b \bigoplus c)]\) рівні 9abc, то\(\bigoplus\) є асоціативним. |
| c. (a # b) # c = a # (b # c); так; Надайте власний приклад, використовуючи цифри. |
| d. (a b) c = a (b c); ні; Надайте свій власний контрприклад, використовуючи цифри. |
| е.\((a \XBox b) \XBox c = a \XBox (b \XBox c)\); Ні; Надайте свій власний лічильник, наприклад, використовуючи цифри. |
| f. (a, b), c = a, (b, c); немає; Надайте свій власний контрприклад, використовуючи цифри. |
| г. (a* b) * c = a * (b * c); немає; Надайте свій власний контрприклад, використовуючи цифри. |
7. а @ (б + с) = (а @ б) + (а @ в)
8. а + (б @ с) = (а + б) @ (а + с)
9.
| а. а & (б $ с) = (а & б) $ (а & с) |
| б. а $ (б & с) = (а $ б) & (а $ c) |
10.
| а. а! (б р в) = (а! б) р (а! в) |
| б. немає |
| c Надайте свій власний лічильник, наприклад, використовуючи цифри. |
| д.\(a \bigoplus (b ! c) = (a \bigoplus b) ! (a \bigoplus c)\) |
| е. ні |
| f Надайте свій власний контрприклад, використовуючи цифри. |
11.
| а.\(a + (b \cdots c) = (a + b) \cdots (a + c)\) |
| б. немає |
| c Надайте свій власний лічильник, наприклад, використовуючи цифри. |
12.
| а.\(a \cdots (b \cdots c) = (a \cdots b) \cdots (a \cdots c)\) |
| б. так |
| c Надайте свій власний приклад, використовуючи цифри. |
13.
| а. а, (б @ с) = (а, б) @ (а, с) |
| б. немає |
| c Надайте свій власний лічильник, наприклад, використовуючи цифри. |
| д. а @ (б, в) = (а @ б), (а @ в) |
| е. ні |
| f Надайте свій власний контрприклад, використовуючи цифри. |
14. Ви самі по собі тут. Проявіть творчість.
15.
a. m n = n n = n m; no; надати свій власний контрприклад з використанням чисел m; no; надати свій власний контрприклад з використанням чисел |
б. м п = п п = п м; так; надайте власні докази м; так; надайте власні докази |
c. (m n) n) x = m x = m (n (n x); немає; надайте свій власний контрприклад, використовуючи числа x); немає; надайте свій власний контрприклад, використовуючи числа |
d. (m n) n) x = m y (n x = m y (n x); немає; надайте свій власний контрприклад x); немає; надайте свій власний контрприклад |
e. a (b + c) = (a (b + c) = (a b) + (a b) + (a c); ні; надати власний контрприклад c); ні; надати власний контрприклад |
f. a (b + c) = (a (b + c) = (a b) + (a b) + (a c); ні; надати власний контрприклад c); ні; надати власний контрприклад |
g. a (b y c) = (a (b y c) = (a b) y (a b) y (a c); ні; надати свій власний контрприклад c); ні; надати свій власний контрприклад |
h. a (b (b c) = (a c) = (a b) b) (a (a c); ні; надати власний контрприклад c); ні; надати власний контрприклад |
16. \((a + b) \cdots c = (a \cdots c) + (b \cdots c)\); так; надати власний приклад
17. \((a \cdots b) + c = (a + c) \cdots (b + c)\); немає; надати свій власний контрприклад
18. \((a + b) \div c = (a \div c) + (b \div c)\); так; надати власний приклад
19. \(a \div (b + c) = (a \div b) + (a \div c)\); немає; надати свій власний контрприклад
20.
a. (b + c) a = (b a = (b a) + (c a) + (c a); ні; надати власний контрприклад a); ні; надати власний контрприклад |
б. (b + c) a = (b a = (b a) + (c a) + (c a); ні; надати власний контрприклад a); ні; надати власний контрприклад |
c. (b c) c) a = (b a = (b a) a) (c (c a); ні; надати власний контрприклад a); ні; надати власний контрприклад |
d. (b c) c) a = (b a = (b a) a) (c (c a); ні; надати власний контрприклад a); ні; надати власний контрприклад |
Рішення для домашніх завдань
1.
| а. 23 | б. 20 | c. 2а + б | д. 26 | г. 2 |
| дж. 90 | м. 1 | с. 10 | с. 26 | v. 17 |
| р. 45 |
2. а. 19
3.
| а. 20 | с. 36 | д. 21 |
Модуль 6 Цілі числа
Набір вправ 1 Рішення
1. {..., -3, -2, -1}
2. {..., -3, -2, -1, 0, 1, 2, 3,...}
3.
| а. 4 | б. 8 | c. 2 | д. 1 | е. 0 |
4.
| а. 7 | б. 13 | c. 4 | д.\(\frac{3}{7}\) | е.\(\frac{3}{7}\) | ф. 6 |
5. а. 6, -6
6. а. 19, -19
7. 0
8. жоден
9.
| а. -5 | б. +3 |
10.
|
а. -3 так як кінцева точка останнього вектора приземлилася на -3.  |
|
б. -9 так як кінцева точка останнього вектора приземлилася на -9.  |
|
c. 4 так як кінцева точка останнього вектора приземлилася на 4.  |
|
d. 1 так як кінцева точка останнього вектора приземлилася на 1.  |
|
е. -2 так як кінцева точка останнього вектора приземлилася на -2.  |
|
f. -60 так як кінцева точка останнього вектора приземлилася на -60.  |
|
g. -1, оскільки кінцева точка останнього вектора приземлилася на -1.  |
|
ч. -3 так як кінцева точка останнього вектора приземлилася на -3.  |
11. термометр
12. ходити два квартали на схід
13. Відповіді на них такі ж, як і для тих, у вправі 10.
14.
| а. 5 | б. -9 | c. -3 | д. 6 |
15.
| а. RRRR | б. ГГ | c. RRRR |
16. 0; причини можуть відрізнятися
17. Відповіді будуть відрізнятися, але завжди буде така ж кількість негативних лічильників, як позитивні лічильники в кожному представленні.
18.
| а. -2 | б. -2 | с. -2 | д. -2 | е. -3 | ф. +3 | г. +3 | ч. +4 |
19. Відповіді будуть відрізнятися, але позитивних лічильників буде на 4 більше, ніж негативних лічильників в кожному поданні.
20. Відповіді будуть відрізнятися, але негативних лічильників буде на 4 більше, ніж позитивні лічильники в кожному поданні.
21.
|
a. (1) Об'єднати 5 червоних та 3 червоних: RRRRRR+RRR (2) Є 8 червоних, RRRRRRRR, що представляє -8. (3) Отже, -5 + -3 = -8. |
|
б. (1) Об'єднати 6 червоних і 9 зелені: RRRRRRRRR+GGGGGGG = Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г (2) Видаліть 6 червоно-зелених пар (нуль), залишивши GGG, який представляє -3. (3) Отже, -6 + 9 = 3. |
|
c. (1) Об'єднати 8 червоних і 6 зелені: RRRRRRRRRRRR+GGGGG = Р Р Р Р Р Р Р Р Г Г Г Г (2) Видаліть 6 червоно-зелених пар (нуль), залишивши RR, який представляє -2. (3) Отже, -8 + 6 = -2. |
|
г. (1) Об'єднати 5 червоних, 3 червоних і 6 зелених: РРРРРР+РРРР+ГГГГГ = Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г (2) Видаліть 6 червоно-зелених пар (нуль), залишивши RR, який представляє -2. (3) Отже, -5 + -3 + 6 = -2. |
|
е. (1) Об'єднати 6 червоних, 9 зелених і 1 червоний: RRRRRRRRR+GGGGGGG+R = Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г (2) Видаліть 7 червоно-зелених пар (нуль), залишивши GG, який представляє +2. (3) Отже, -6 + 9 + -1 = +2. |
|
f. (1) З'єднати 4 зелені, 6 зелені і 5 червоних: GGGGG+GGGGGG+РРРРР = Г Г Г Г Г Г Г Г Г Г Г Р Р Р Р Р Р (2) Видаліть 5 червоно-зелених пар (нуль), залишивши GGGGG, який представляє +5. (3) Отже, +4 + +6 + -5 = +5. |
22.
|
а. (1) 6 - 3 означає видалити 3 зелені з колекції лічильників, що представляють 6. (2) Представляємо 6 із зеленню 6: GGGGGG (3) Видаліть 3 зелені, залишивши GGG, який представляє +3. (4) Отже, 6 - 3 = 3 |
|
б. (1) 4 - 6 означає видалити 6 зелені з колекції лічильників, що представляють 4. (2) Представляємо 4 з 4 зеленню: GGGG (3) Додайте 2 червоно-зелені пари (нуль) до колекції: Г Г Г Г Г Г Г Р Р (4) Видаліть 6 зелені, залишивши RR, який представляє -2. (5) Отже, 4 - 6 = -2 |
|
c. (1) -7 - -6 означає видалити 6 червоних з колекції лічильників, що представляють -7. (2) Представляють -7 з 7 червоними: RRRRRR (3) Видаліть 6 червоних, залишивши R, який представляє -1. (4) Отже, -7 - (-6) = -1 |
|
d. (1) -3 — -7 означає видалити 7 червоних з колекції лічильників, що представляють -3. (2) Представляють -3 з 3 червоними: RRR (3) Додайте 4 червоно-зелені пари (нуль) до колекції: Р Р Р Р Р Р Р Р Г Г Г Г (4) Видаліть 7 червоних, залишивши GGGG, який представляє +4. (5) Отже, -3 - (-7) = +4 |
|
е. (1) 4 - -3 означає видалити 3 червоні з колекції лічильників, що представляють +4. (2) Представляють +4 з 4 зеленню: GGGG (3) Додайте до колекції 3 червоно-зелені пари (нуль): Г Г Г Г Г Г Г Г Г Р Р Р (4) Видаліть 3 червоних, залишивши GGGGGGG, який представляє +7. (5) Отже, 4 - (-3) = +7 |
|
f. (1) -2 - 5 означає видалити 5 зелені з колекції лічильників, що представляють -2. (2) Представляють -2 з 2 червоними: RR (3) Додати 5 червоно-зелених пар (нуль) до колекції: Р Р Р Р Р Р Р Г Г Г Г Г Г (4) Видаліть 5 зелені, залишивши RRRRRRR, який представляє -7. (5) Отже, -2 - 5 = -7 |
|
г. (1) 5 - 5 означає видалити 5 зелені з колекції лічильників, що представляють 5. (2) Представляємо 5 із зеленню 5: GGGG (3) Видаліть 5 зелені, не залишаючи нічого, що представляє 0. (5) Тому, 5 - 5 = 0 |
|
h. (1) 5 - (-5) означає видалити 5 червоних з колекції лічильників, що представляють 5. (2) Представляємо 5 із зеленню 5: GGGG (3) Додати 5 червоно-зелених пар (нуль) до колекції: Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Р Р Р (4) Видаліть 5 червоних, залишивши GGGGGGGGGG, який представляє 10. (5) Отже, 5 - (-5) = +10 |
|
i. (1) -4 — (- 4) означає видалити 4 червоні з колекції лічильників, що представляють -4. (2) Представляють -4 з 4 червоними: RRRR (3) Видаліть 4 червоні, не залишаючи нічого, що представляє 0.. (5) Отже, -4 — -4 = 0. |
|
j. (1) -6 - 6 означає видалити 6 зелені з колекції лічильників, що представляють -6. (2) Представляють -6 з 6 червоними: RRRRRR (3) Додайте до колекції 6 червоно-зелених пар (нуль): Р Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г (4) Видаліть 6 зелені, залишивши RRRRRRRRRRRRR, який представляє -12. (5) Отже, -6 - 6 = -12 |
23.
|
а. (1) 5 - 8 означає видалити 8 зелені з колекції лічильників, що представляють 5. (2) Представляємо 5 із зеленню 5: GGGG (3) Додайте до колекції 3 червоно-зелені пари (нуль): Г Г Г Г Г Г Г Г Г Г Г Г Р Р (4) Видаліть 8 зелені, залишивши RRR, який представляє -3. (5) Отже, 5 - 8 = -3 |
|
б. (1) 5 + -8 означає об'єднати 5 зелені і 8 червоних: ГГГГГГ+РРРРРРРР = Г Г Г Г Г Р Р Р Р Р Р Р Р Р Р Р Р Р Р (2) Видаліть 5 червоно-зелених пар (нуль), залишивши RRR, який представляє -3. (3) Отже, 5 + -8 = -3. |
| c Відповіді однакові. |
24. Існують різні способи вирішення цієї проблеми. Але в будь-якому випадку підсумковий збір для кожного повинен дати однакову відповідь.
25.
|
a. 1-й спосіб: Видаліть 3 зелені з колекції, що представляє -5. 2-й спосіб: Об'єднайте колекцію з 5 червоних і 3 червоних разом. |
|
б. 1-й спосіб: Видаліть 8 зелені з колекції, що представляє +4. 2-й спосіб: З'єднайте збір з 4 зелені і 8 червоних разом. |
|
c. 1-й спосіб: Видалити 7 червоних з колекції, що представляє -9. 2-й спосіб: З'єднайте колекцію з 9 червоних і 7 зелені разом. |
|
d. 1-й спосіб: Видалити 10 червоних з колекції, що представляє -10. 2-й спосіб: З'єднайте колекцію з 10 червоних і 10 зелені разом. |
26.
| а. 4 + (-5) | б. -9 + (-7) | с. -3 + (+4) |
27.
| а. 4 + -5 + -7 + -6 + +9 | б. -43 + (+75) + 12 + 63 + (-9) |
28.
| а. -6 | б. +8 | c. негативний, негативний | d. позитивний, позитивний | е. навпроти |
29.
| а. коли зменшене і віднімане одне і те ж число | б. 0 |
30.
|
а. 10 — 4 = +6  |
е. 3 — 10 = -7  |
|
б. -7 — 5 = -12  |
ф. -5 — (-8) = +3  |
|
c. 8 — (-3) = +11  |
г. 6 — (-6) = +12  |
|
д. -9 — -1 = -8  |
ч. 9 — 9 = 0  |
31.
| а. 1 — (-5) = +6 | б. 13 — 10 = +3 | в. 3 — 8 = -5 |
32.
| а. -92 — -71 = -21 | д. -122 — 76 = -198 |
| б. 92 — -81 = +173 | е. 208 — 389 = -181 |
| в. -110 — -200 = +90 | а. 46 + -76 + 92 = 138 + -76 = 62 |
33.
| а. 46 + -76 + 92 = -30 + 92 = 62 |
| б. -63 + 94 + 45 + -71 = 31 + 45 + -71 = 76 + -71 = 5 |
34.
| а. 46 + -76 + 92 = 138 + -76 = 62 |
| б. -63 + 94 + 45 + -71 = 139 + -134 = 5 |
35.
| а. закрито |
| а. закрито |
| а. закрито |
| d. не закритий; один контрприклад: 7 - 10 = -3 |
| е Закрито |
| f. не закритий; один контрприклад: -11 — -20 = +9 |
| г. не закритий; один контрприклад: 1 + 1 = 2 |
| h. не закритий; один контрприклад: 1 — -1 = 2 |
Набір вправ 2 Рішення
1.
| а. р р р р р г |
| б Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Р Р Р Р Р Р Р Р Р Р Р Р Р Р |
| с. РРРРРРРРРР = -12 |
2.
| а. р р р р р р г г |
| б Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г Г Г Г Г Р Р Р Р Р Р Р Р Р Р Р Р |
| с. РРРРРРРРРР = -12 |
3.
| а. р р р р р |
| б Р Р Р Р Р Р Р Р Р Р Р Р Р |
| с. -12 |
4.
| а.\(4 \times -2\) означає об'єднати 4 комплекти по 2 червоних: РР+ РР+ РР+ РР = РРРРРРРР = -8 |
| б.\(3 \times 5\) означає об'єднати 3 набори по 5 зелені: GGGGGG+GGGGG + GGGGG = GGGGGGGGGGG = +15 |
| c.\(5 \times -3\) означає об'єднати 5 наборів з 3 червоних: РРРР+РРРР+РРРР+РРР = RRRRRRRRRRRR = -15 |
| д.\(7 \times 2\) означає об'єднати 7 наборів по 2 зелені: ГГ+ ГГ+ГГ+ГГ+ГГ+ГГ+ ГГ+ГГ = ГГГГГГГГГГГГГГГГГ = +14 |
| е.\(0 \times -3\) означає об'єднати 0 наборів з 3 червоних = 0 |
5.
| А Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г |
| б Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Р Р Р Р Р Р Р Р Р Р Р Р Р |
| в Р Р Р Р Р Р Р Р Р Р Р Р Р = -12 |
6.
| А Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г |
| б Р Р Р Р Р Р Р Р Р Р Р Р Р |
| с. -12 |
7.
|
а.\(-5 \times 3\) означає, щоб видалити 5 наборів 3 зелені з колекції, що представляє нуль. (1) Нехай нуль буде представлений 15 червоними і 15 зеленню: Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г (2) Видаліть 5 наборів 3 зелені з вищевказаної колекції, яка залишає RRRRRRRRRRRR, який представляє -15. Тому,\(-5 \times 3 = -15\). |
|
б.\(-3 \times 2\) означає видалити 3 набори 2 зелені з колекції, що представляє нуль. (1) Нехай нуль буде представлений 6 червоними та 6 зеленими: Р Р Р Р Р Р Р Р Г Г Г Г Г Г (2) Видаліть 3 набори 2 зелені з вищевказаної колекції, яка залишає RRRRRR, який представляє -6. Тому,\(-3 \times 2 = -6\) |
| c.\(2 \times -3\) означає об'єднати 2 комплекти по 3 червоних: RRRR+RRR = RRRRRR = -6. Тому\(2 \times -3 = -6\) |
|
d.\(-2 \times 3\) означає видалити 2 набори 3 зелені з колекції, що представляє нуль. (1) Нехай нуль буде представлений 6 червоними і 15 зеленню: Р Р Р Р Р Р Р Р Г Г Г Г Г Г (2) Видаліть 2 набори 3 зелені з вищевказаної колекції, яка залишає RRRRRR, що представляє -6. Тому,\(-2 \times 3 = -6\). |
| е.\(3 \times 2\) означає об'єднати 3 набори по 2 зелені: GG+ GG+ GG = GGGGGG = 6. Тому\(3 \times 2 = 6\) |
| f.\(0 \times -4\) означає об'єднати 0 наборів з 4 червоних = 0 |
|
g.\(-4 \times 0\) означає вилучити 4 набори 0 лічильників з колекції, що представляє нуль. (1) Виберіть будь-яке представлення нуля. Одна з можливостей полягає в тому, щоб нуль був представлений 6 червоними і 6 зеленими. Р Р Р Р Р Р Р Р Г Г Г Г Г Г (2) Вилучити 0 наборів 0 лічильників з наведеної вище колекції, яка залишає початкову колекцію, яка представляє 0. Тому,\(-4 \times 0 = 0\). |
8.
\(-3 \times 6\): Видаліть 3 набори 6 зелені з нуля; 5G і 23R; -18
\(-3 \times 6\): Видалити 3 набори 6 зелені з нуля; 18R; -18
\(-4 \times 4\): Видалити 4 набори 4 зелені з нуля; 2G і 18R; -16
\(-4 \times -4\): Видалити 4 набори 4 червоних з нуля; 18G і 2R; 16
\(-5 \times 2\): Видалити 5 наборів 2 зелені з нуля; 4G і 14R; -10
\(-2 \times 5\): Видалити 2 набори 5 зелені з нуля; 3G і 13R; -10
\(-5 \times -2\): Видалити 5 наборів 2 червоних з нуля; 11G і 1R; 10
\(-2 \times -5\): Видалити 2 набори 5 червоних з нуля; відповіді будуть змінюватися; 10
\(-3 \times 3\): Видалити 3 набори 3 зелені з нуля; 1G і 10R; -9
\(-3 \times -3\): Видалити 3 набори 3 червоних з нуля; 12G і 3R; 9
\(-7 \times 2\): Видалити 7 наборів 2 зелені з нуля; відповіді будуть відрізнятися; -14
\(-2 \times 8\): Видалити 2 набори 8 зелені з нуля; 2G і 18R; -16
\(-2 \times -8\): Видалити 2 набори 8 червоних з нуля; 18G і 2R; 16
9.
| a. позитивний | б. негативний | c. нуль | d. позитивний |
10.
| а. закрито |
| б. закрито |
| c Не закрито: один контрприклад:\(-2 \times -8 = 16\) |
| d. не закрито: один контрприклад:\(-1 \times -1 = 1\) |
| е Закрито |
| f. закрито |
11.
| a. правда |
| б. правда |
| c. правда |
| d. брехня; 2 < 3; помножити обидві сторони на 5:\(2 \times 5 > 3 \times 5\) помилково. |
| e. правда |
| f. false: 2 < 3; Помножте обидві сторони на -5:\(2 \times -5 > 3 \times -5\) помилково. |
12.
| а Якщо a > b і b > c, то a > c |
| b Якщо a > b, то a + c > b + c |
| c Якщо a > b, то ap > bp |
| d Якщо a > b, то an < bn |
Рішення для домашніх завдань
2.
| а. 16 | c. 2 | д. 8 |
3. а. 4 і -4
4.
| а. +7 | с. -9 |
5.
| а. 2 — (-5) | с. 3 — 12 |
6. -8 + 5 + (-3) = -6, так як кінцева точка останнього вектора приземлилася на -6.

8.
|
а. 5 - 11 = -6  |
|
в. 5 - (-11) = 16  |
9.
а. (1) -4 + (-3) означає поєднання 4 червоних і 3 червоних: RRRRR+RRR = RRRRRR, що представляє -7
(2) Отже, -4 + -3 = -7
10.
а. (1) 6 - 8 означає видалити 8 зелені з колекції лічильників, що представляють +6.
(2) Представляють +6 із зеленню 6: GGGGGG
(3) Додайте 2 червоно-зелені пари (нуль) до колекції:
Г Г Г Г Г Г Г Г
Р Р
(4) Видаліть 8 зелені, залишивши RR, який представляє -2.
(5) Отже, 6 - 8 = -2
11.
| а. закрито |
| б. не закритий; контрприклад - 3 — 10 = -7 |
| c Закрито |
12.
а.\(-5 \times 3\) означає, щоб видалити 5 наборів 3 зелені з колекції, що представляє нуль.
(1) Нехай нуль буде представлений 15 червоними і 15 зеленню:
Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р
Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г
(2) Видаліть 5 наборів 3 зелені з вищевказаної колекції, яка залишає
RRRRRRRRRRRR, який представляє -15. Тому,\(-5 \times 3 = -15\).
Рішення для домашніх завдань
2.
| а. 16 | c. 2 | д. 8 |
3. а. 4 і -4
4. а. +7
5.
| а. 2 — (-5) | с. 3 — 12 |
6. -8 + 5 + -3 = -6, так як кінцева точка останнього вектора приземлилася на -6.

8.
|
а. 5 - 11 = -6  |
|
в. 5 - (-11) = 16  |
9.
a. (1) -4 + -3 означає об'єднати 4 червоних і 3 червоних: RRRRR+RRR = RRRRRR, що представляє -7
(2) Отже, -4 + -3 = -7
10.
а. (1) 6 - 8 означає видалити 8 зелені з колекції лічильників, що представляють +6.
(2) Представляють +6 із зеленню 6: GGGGGG
(3) Додайте 2 червоно-зелені пари (нуль) до колекції:
Г Г Г Г Г Г Г Г
Р Р
(4) Видаліть 8 зелені, залишивши RR, який представляє -2.
(5) Отже, 6 - 8 = -2
11.
| а. закрито |
| б. не закритий; контрприклад - 3 — 10 = -7 |
| c Закрито |
12.
а.\(-5 \times 3\) означає, щоб видалити 5 наборів 3 зелені з колекції, що представляє нуль.
(1) Нехай нуль буде представлений 15 червоними і 15 зеленню:
Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р
Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г Г
(2) Видаліть 5 наборів 3 зелені з вищевказаної колекції, яка залишає RRRRRRRRRRRRR, що представляє -15. Тому,\(-5 \times 3 = -15\).
Модуль 7 Відділ
Набір вправ 1 Рішення
1.
| а. 2 | б. р | c. р, Р |
2.
|
а. Р, Ш, П, Ш 9, 2, 4, 1, 9, 4, 2, 1  |
|
б Л, Р, Л, Р, 11, 3, 3, 2, 11, 3, 3, 2  |
|
c. R, порожній (або 0), R, порожній (або 0), 8, 4, 2, порожній (або 0), 8, 2, 4, порожній (або 0)  |
|
д. ш, Л, Ш, Л, 7, 4, 1, 3, 7, 1, 4, 3  |
|
е. R, порожній (або 0), R, порожній (або 0), 6, 3, 2, порожній (або 0), 6, 2, 3, порожній (або 0)  |
3. 2 рівні палі по 18 одиниць кожна

4.
| а.\(210_{\text{four}\) |
| b Методи будуть відрізнятися. |
| c.\(102_{\text{four}}\) |
| д.\(210_{\text{four}}, 102_{\text{four}}\) |
5.
| а.\(1100_{\text{three}}\) |
| b Методи будуть відрізнятися. |
| c.\(200_{\text{three}}\) |
| д.\(1100_{\text{three}}, 200_{\text{three}}\) |
7.
| а.\(210_{\text{four}}\) |
| b Методи будуть відрізнятися. |
| c.\(30_{\text{four}}\) |
| д.\(210_{\text{four}}, 30_{\text{four}}\) |
9.
| а.\(100 \div 4\) |
| b. поділ на підмножини |
| c Виплачувати 100 мармурів на 4 рівні підмножини. |
|
д.  |
| е.\(4 \cdots 25\) |
| f Підрахуйте, скільки кульок було поміщено в одну з рівних підмножин. |
| г. 25 |
10.
| а.\(80 \div 8\) |
| b. повторне віднімання |
| c Покладіть 8 унцій у підмножині за один раз. |
|
д.  |
| е.\(10 \cdots 8\) |
| f Підрахуйте, скільки підмножин, кожна з яких має 8 унцій, було зроблено. |
| г. 10 |
11.
| а.\(144 \div 16\) |
| b. повторне віднімання |
| c. відраховуйте 16 сторінок за раз. |
|
д.  |
| е.\(9 \cdots 16\) |
| f Порахуйте, скільки коротких оповідань, кожна з яких має 16 сторінок, було зроблено. |
| г. 9 |
12.
| а.\(500 \div 4\) |
| b. поділ на підмножини |
| c Виплачуйте 500 доларів на 4 рівні підмножини. |
|
д.  |
| е.\(4 \cdots 125\) |
| f Підрахуйте, скільки грошей було поміщено в одну з рівних підмножин. |
| г. 125$ |
13.
| а.\(8 \div 1\frac{1}{3}\) |
| b. повторне віднімання |
| c Покладіть 1\(\frac{1}{3}\) чашку в підмножину за раз. |
|
д.  |
| е.\(6 \cdots 1\frac{1}{3}\) |
| f Підрахуйте, скільки підмножин було утворено. |
| г. 6 |
14.
| а.\(65 \div 13\) |
| b. поділ на підмножини |
| c Виплачувати 65 бейсболів в 13 рівних підмножин. |
|
д.  |
| е.\(13 \cdots 5\) |
| f Підрахуйте, як бейсбольні кулі були розміщені в одній з рівних підмножин. |
| г. 5 |
15.
|
д.  |
| е.\(12 \cdots 4\) |
|
г.  |
| ч.\(4 \cdots 12\) |
16.
|
д.  |
| е.\(4 \cdots 50\) |
| г Помістіть 4 в підмножину одночасно. |
| ч.\(50 \cdots 4\) |
17.
| d Намалюйте 50 підмножин, а потім розподіліть 150 серед 50 підмножин. |
| е.\(50 \cdots 3\) |
|
г.  |
| ч.\(3 \cdots 50\) |
18.
| d Намалюйте 35 підмножин, а потім розподіліть 140 серед 35 підмножин. |
| е.\(35 \cdots 4\) |
|
г.  |
| ч.\(4 \cdots 35\) |
19.
|
д.  |
| е.\(5 \cdots 19\) |
| г Помістіть 5 в підмножину одночасно. |
| ч.\(19 \cdots 5\) |
19.
|
д.  |
| е.\(5 \cdots 19\) |
| г Помістіть 5 в підмножину одночасно. |
| ч.\(19 \cdots 5\) |
19.
|
д.  |
| е.\(5 \cdots 19\) |
| г Помістіть 5 в підмножину одночасно. |
| ч.\(19 \cdots 5\) |
22.
| а.\(56 \div 8\) |
| б.\(40 \div 5\) |
23.
| а.\(18 \div 9\) |
| б.\(10 \div 2\) |
24. a представляє, скільки підмножин і b представляє, скільки в кожній підмножині.
25.
| а. оскільки 32 = 8\(\cdots\) 4, то\(32 \div 8\) = 4 |
| б. з 56 = 8\(\cdots\) 7, то 56\(\div\) 8 = 7 |
| с. з 32 = 2\(\cdots\) 16, то 32\(\div\) 2 = 16 |
| d Оскільки 0 = 13\(\cdots\) 0, то 0\(\div\) 13 = 0 |
| е. з 12 = 1\(\cdots\) 12, то 12\(\div\) 1 = 12 |
| f Оскільки Х = 1\(\cdots\) Х, то Х\(\div\) 1 = Х |
| г Оскільки 0 = Y\(\cdots\) 0, то 0\(\div\) Y = 0 |
26.
| с. з 48 = 6\(\cdots\) 8, то 48\(\div\) 6 = 8 |
| d Оскільки не існує цілого числового рішення, щоб зробити рівняння 35= 4\(\cdots\) __ істинним, 35\(\div\) 4 не визначається під цілими числами. |
| е. з 48 = 1\(\cdots\) 48, то 48\(\div\) 1 = 48 |
| f Оскільки не існує цілого числового рішення, щоб зробити рівняння 55 = 7\(\cdots\) __ істинним, 55\(\div\) 7 не визначається під цілими числами. |
| г Оскільки 0 = 8\(\cdots\) 0, то 0\(\div\) 8 = 0 |
| д. 203 р. 314 |
| ф. 248 р. 14 |
27.
| а. немає числа, яке зробить рівняння, 6 = 0\(\cdots\) ____ істинним, оскільки будь-яке число, поставлене в порожнє, зробить праву частину рівняння нулем, що ніколи не може дорівнювати лівій стороні рівняння, яка дорівнює 6. Тому\(6 \div 0\) не визначено. |
| б. немає числа, яке зробить рівняння, 18 = 0\(\cdots\) ____ істинним, оскільки будь-яке число, поставлене в порожнє, зробить праву частину рівняння нулем, що ніколи не може дорівнювати лівій стороні рівняння, яка дорівнює 18. Тому\(18 \div 0\) не визначено. |
| c Немає числа, яке зробить рівняння, M = 0\(\cdots\) ____ істинним, оскільки будь-яке число, поставлене в порожнє, зробить правою стороною рівняння нуль, що ніколи не може дорівнювати лівій стороні рівняння, яка є M (оскільки передбачається, що M не дорівнює нулю). Тому\(M \div 0\) не визначено. |
Набір вправ 2 Рішення
1.
| а. 6 р. 43 |
| б. 7 р. 20 |
| c. 8 р. 8 |
| д. 3 р. 194 |
| е. 5 р. 55 |
| ф. 5 р. 165 |
| г. 9 р. 239 |
2.
| а. 45 р. 15 |
| б. 12 р. 27 |
| в. 32 р. 34 |
| д. 81 р. 29 |
3.
| а. 45 р. 15 |
| б. 12 р. 27 |
| в. 32 р. 34 |
| д. 81 р. 29 |
| д. 203 р. 314 |
| ф. 248 р. 14 |
Набір вправ 3 Рішення
1.
| а. Ф Ф Л Л У |
|
б. i. ЛУУ, ЛУУ, ЛУУ, ЛУУ, ЛУУ II. У |
| c. УУУУУ |
| d. частка: LUU, залишок: U |
| е.\(12_{\text{three}}r. 1_{\text{three}}\) |
| ф.\(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three}} = 222_{\text{three}}\) |
2.
| а.\(13_{\text{five}}r. 3_{\text{five}}\) |
| б.\(32_{\text{six}}r. 21_{\text{six}}\) |
| c.\(11_{\text{four}}r. 10_{\text{four}}\) |
| д.\(110_{\text{two}}r. 1_{\text{two}}\) |
3.
| а.\(23_{\text{seven}}r. 3_{\text{seven}}\) |
| б.\(102_{\text{three}}\) |
Набір вправ 3 Рішення
1.
| а. Ф Ф Л Л У |
|
б. i. ЛУУ, ЛУУ, ЛУУ, ЛУУ, ЛУУ II. У |
| c. УУУУУ |
| d. частка: LUU, залишок: U |
| е.\(12_{\text{three}}r. 1_{\text{three}}\) |
| ф.\(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three }}= 222_{\text{three}}\) |
2.
| а.\(13_{\text{five}}r. 3_{\text{five}}\) |
| б.\(32_{\text{six}}r. 21_{\text{six}}\) |
| c.\(11_{\text{four}} r. 10_{\text{four}}\) |
| д.\(110_{\text{two}} r. 1_{\text{two}}\) |
3.
| а.\(23_{\text{seven}}r. 3_{\text{seven}}\) |
| б.\(102_{\text{three}}\) |
4. \(12_{\text{three}}r. 1_{\text{three}}\)
5. \(13_{\text{five}}r. 3_{\text{five}}\)
6. \(11_{\text{four}}r. 10_{\text{four}}\)
7. \(32_{\text{six}}r. 21_{\text{six}}\)
8. \(110_{\text{two}}r. 1_{\text{two}}\)
9. \(23_{\text{seven}}r. 3_{\text{seven}}\)
10. \(102_{\text{three}}\)
11. \(31_{\text{five}}r. 2_{\text{five}}\)
12. \(111_{\text{two}}r. 101_{\text{two}}\)
13. \(61_{\text{eight}}r. 6_{\text{eight}}\)
14. \(T2_{\text{thirteen }}r. E_{\text{thirteen}}\)
15. \(23_{\text{twelve}}r. 1E_{\text{twelve}}\)
Рішення для домашніх завдань
1.
| а.\(72 \div 4\) |
| b. повторне віднімання |
| c Покладіть 4 льодяники в мішок одночасно, неодноразово віднімаючи 4 з 72, поки не закінчаться льодяники. |
|
д.  |
| е.\(18 \cdots 4\) |
| f Підрахуйте, скільки підмножин з 4 ви зробили, скільки там мішків льодяників. |
| г. 18 |
7.
|
а.  |
|
б.  |
| c Розбиття на підмножини простіше, тому що вам потрібно зробити лише 2 рівні підмножини, на відміну від віднімання 2 за раз. |
11.
| a. кількість підмножин |
| b. кількість в кожній підмножині |
13. \(56_{\text{seven}}r. 22_{\text{seven}}\)
15. \(285_{\text{eleven}}r. 167_{\text{eleven}}\)
17. \(2111_{\text{three}}r. 210_{\text{three}}\)
18.
| а. не закритий;\(-1 \div -1 = 1\) |
| c. не закрито;\(1 \div 0\) не визначено |
19. Ні;\(10 \div 2 = 5\), але\(2 \div 10 = 1/2\). Тому,\(10 \div 2 \nleq 2 \div 10\). Використовуйте інший приклад лічильника у своїх відповідях.
Модуль 8 Теорія чисел
Набір вправ 1 Рішення
1.
| а. 7 | б. 3 |
| c. 8 | д. 1 |
| е. 2 | ф. 8 |
| г. 2 | ч. 8 |
| i. 0 | Дж. 2 |
| к.4 | л. 0 |
| м. 7 | п. 8 |
2. ті ж відповіді, що і для вправи 1
3. Так.
4.
|
а. кк: 6 + 7 = 13 → 4 \(4 \nleq 2\); помилка |
|
б. см: 5 + 1 = 6 6 = 6; правильно |
|
с.к.: 2 + 3 = 5 \(5 \nleq 4\); помилка |
|
д Ск: 8 + 2 + 5 = 15 → 6 6 = 6; правильно |
|
е. кк: 5 + 2 + 2 = 9 → 0 \(0 \nleq 3\); помилка |
|
ф. см: 1 + 7 + 0 = 8 8 = 8; правильно |
5.
|
а.\(2 \cdots 8 = 16 → 7\) 7 = 7; правильно |
|
б.\(2 \cdots 0 = 0\) \(0 \nleq 8\); помилка |
|
c.\(5 \cdots 1 = 5\) 5 = 5; правильно |
|
д.\(2 ·\cdots 7 = 14 → 5\) \(5 \nleq 4\); помилка |
|
е.\(0 \cdots 1 = 0\) 0 = 0; правильно |
|
ф. 3 · 7 = 21 → 3 \(3 \nleq 4\); помилка |
|
г.\(2 \cdots 7 = 14 → 5\) 5 = 5; правильно |
|
ч.\(5 \cdots 2 = 10 → 1\) \(1 \nleq 0\); помилка |
|
я.\(2 \cdots 6 = 12 → 3\) 3 = 3; правильно |
6. Виконуйте проблеми, а потім перевірте свої відповіді за допомогою цифрових коренів.
7.
|
а. 0 + 5 = 5 5 = 5; правильно |
|
б. 8 + 0 = 8 8 = 8; правильно |
|
c. 5 + 3 = 8 \(8 \nleq 6\); помилка |
|
д. 8 + 6 = 14 → 5 \(5 \nleq 4\); помилка |
|
е. 5 + 4 = 9 → 0 0 = 0; правильно |
|
ф. 1 + 4 = 5 5 = 5; правильно |
8. Виконуйте проблеми, а потім перевірте свої відповіді за допомогою цифрових коренів.
9.
|
а.\(1 \cdots 4 = 4; 4 + 7 = 11 → 2\) 2 = 2; правильно |
|
б.\(6 \cdots 0 = 0; 0 + 0 = 0\) 0 = 0; правильно |
|
c.\(8 \cdots 8 = 64 → 10 → 1; 1 + 1 = 2\) \(2 \nleq 4\); помилка |
|
д.\(6 \cdots 3 = 18 → 0; 0 + 5 = 5\) 5 = 5; правильно |
10. Вирішіть проблему, а потім перевірте свою відповідь за допомогою цифрових коренів.
11.
| а Це проблема поділу. Відповідь - 5. |
| б Це помилкове твердження, оскільки 35 не є коефіцієнтом 7. |
| c Це вірне твердження, оскільки 7 - коефіцієнт 35; (\(7 \cdots 5 = 35\)) |
| d Це проблема поділу. Відповідь - 5 р. 5. |
| е. це помилкове твердження, оскільки 56 не є коефіцієнтом 8. |
| f Це помилкове твердження, оскільки 7 не є коефіцієнтом 40. |
| g Це вірне твердження, оскільки 12 - коефіцієнт 60; (\(12 \cdots 5 = 60\)) |
| h Це проблема поділу. Відповідь - 2 р. 20. |
| i. Це проблема поділу. Відповідь - 14. |
| j Це помилкове твердження, оскільки 42 не є коефіцієнтом 3. |
| k. це вірне твердження, оскільки 6 - коефіцієнт 42; (\(6 \cdots 7 = 42\)) |
| l Це проблема поділу. Відповідь - 8. |
| м. це проблема поділу. Відповідь - 50. |
| n. це вірне твердження, оскільки 4 - коефіцієнт 100; (\(4 \cdots 25 = 100\)) |
| o Це помилкове твердження, оскільки 4 не є коефіцієнтом 90. |
| п. це помилкове твердження, оскільки 25 не є коефіцієнтом 5. |
13. Доказ пишеться точно так само, як приклад 1, показаний вище цієї вправи, якщо a замінено на x, b замінено на y, а c замінено на z.
18. Якщо a - множник b, то am = b для деякого цілого числа, m Якщо a - множник c, то an = c для деякого цілого числа n. використовуючи підстановку, bc = (am) (an) = a (amn), що показує a - множник bc.
19. Доказ пишеться точно так само, як у прикладі, показаному вище цієї вправи, якщо a замінено на c, b замінено на a, а c замінено на b.
20.
| a. 2|9,712 оскільки остання цифра парна. |
| б. 5,643 непарна, тому вона не ділиться на 2. |
| c. 5 690 не ділиться на 4, оскільки 4 не є коефіцієнтом 90. |
| d. 63 868 ділиться на 4, оскільки 4 - коефіцієнт 68. |
| е. 854 100 ділиться на 4, оскільки 4 - коефіцієнт 0. |
| f. 8 - коефіцієнт 12 345 248, оскільки 8 - коефіцієнт 248. |
| г. 54 094 422 не ділиться на 8, оскільки 8 не є коефіцієнтом 422. |
21.
| a. 5|9,750 з моменту останнього 0. |
| б. 5|5 645 з моменту останнього 5. |
| c. 5 696 не ділиться на 5, оскільки остання цифра не дорівнює 0 або 5. |
| d. 10|63 860, оскільки остання цифра дорівнює 0. |
| е. 854,105 не ділиться на 10, оскільки остання цифра не дорівнює 0. |
22.
| a. 3|9,750 починаючи з 3|3, де 3 - цифровий корінь 9,750. |
| b. 3|5,645 є помилковим, оскільки 3 не є коефіцієнтом 2, що є д.р. 5,645. |
| c. 3|5,696 є помилковим, оскільки 3 не є коефіцієнтом 8, д.р. 5,696. |
| d. 3|63 860 є помилковим, оскільки 3 не є коефіцієнтом 5, д.р. 63,860. |
| е. 3|854,115 з 3|6, де 6 - д.р. з 854 115. |
23.
| a. 9|9,753 є помилковим, оскільки цифровий корінь 9,753 дорівнює 6, а не 0. |
| б. 9|5,646 є хибним, оскільки д.р. з 5,646 дорівнює 3, а не 0. |
| c. 9|5,697, оскільки цифровий корінь 5,697 дорівнює 0. |
| d. 9|63 576 оскільки цифровий корінь 63,576 дорівнює 0. |
| е. 9|854,103 є помилковим, оскільки д.р. з 854,103 дорівнює 3, а не 0. |
24.
| a. 6|9,753 є помилковим, оскільки 9,753 не є парним, тому не ділиться на 2. |
| b. 6|5,645 є помилковим, оскільки 5,645 не є парним, тому не ділиться на 2. |
| c. 6|5,696 є помилковим, оскільки 3 не є коефіцієнтом 8, що є д.р. 5,696. |
| d. 6|63,876 оскільки він парний і також ділиться на 3, оскільки dr. 3. |
| е. 6|854,103 є помилковим, оскільки 854,103 не є парним, тому не ділиться на 2. |
25.
| a. 15|9,753 є помилковим, оскільки він не ділиться на 5. |
| б. 15|6,645, оскільки і 3, і 5 є факторами. |
| c. 15|1,690 є помилковим, оскільки 3 не є фактором. |
| d. 15|63,872 є помилковим, оскільки 5 не є фактором. |
| е. 15|654,105 оскільки він ділиться як на 3, так і на 5. |
26. Включити обґрунтування
| a. правда |
| б. помилковий |
| c. правда |
| d. правда |
27. Включити обґрунтування
| a. правда |
| б. помилковий |
| c. помилковий |
| d. правда |
| e. помилковий |
Набір вправ 2 Рішення
1. с. 1, 2, 3, 4, 6, 12
2.
| а. 1, 2 |
| б. 1, 3 |
| с. 1, 2, 4 |
| д. 1, 5 |
| е. 1, 2, 3, 6 |
| г. 1, 2, 4, 8 |
| ч. 1, 3, 9 |
| i. 1, 2, 5, 10 |
| д. 1, 11 |
| к. 1, 13 |
| л. 1, 2, 7, 14 |
| м. 1, 3, 5, 15 |
| п. 1, 2, 4, 8, 16 |
3.
| а. 2, 3, 5, 7, 11, 13 |
| б. єдиними факторами є 1 і саме число. |
| с. 4, 9, 16 |
| d. вони ідеальні квадрати. |
4.
| а.\(45 = 3 \cdots 3 \cdots 5\) |
| б.\(65 = 5 \cdots 13\) |
| c.\(200 = 2 \cdots 2 \cdots 2 \cdots 5 \cdots 5\) |
| д.\(91 = 7 \cdots 13\) |
| е.\(76 = 2 \cdots 2 \cdots 19\) |
| ф.\(350 = 2 \cdots 5 \cdots 5 \cdots 7\) |
| г.\(189 = 3 \cdots 3 \cdots 3 \cdots 7\) |
| ч.\(74 = 2 \cdots 37\) |
| я.\(512 = 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2\) |
| j.\(147 = 3 \cdots 7 \cdots 7\) |
5. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
6. 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48
7. 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108 10, 11, 112, 14, 15, 116, 117, 18, 119, 120
8. \(11 \cdots 47\)
9. 22,7
10.
| а. 11; 149 |
| б. 13; 3 · 7 · 13 |
| с. 19; 3 · 127 |
| д. 19; 19 · 23 |
| д. 19; 509 |
| ф. 23; 613 |
| г. 23; 787 |
11.
| а.\(2 \cdots 2 \cdots 2 \cdots 5 \cdots 7\) |
| б. 281 |
| c.\(2 \cdots 3 \cdots 47\) |
| д. 283 |
| е.\(2 \cdots 2 \cdots 71\) |
| ф.\(5 \cdots 3 \cdots 19\) |
| г.\(2 \cdots 11 \cdots 13\) |
| ч.\(7 \cdots 41\) |
| я.\(25 \cdots 3 \cdots 3\) |
| j.\(17 \cdots 17\) |
| к.\(2 \cdots 5 \cdots 29\) |
| л.\(3 \cdots 97\) |
| м.\(2 \cdots 2 \cdots 73\) |
| п. 293 |
| o.\(2 \cdots 3 \cdots 7 \cdots 7\) |
| р.\(5 \cdots 59\) |
12. 281 і 283
13. Ні; принаймні один буде кратний 3.
14.
| а. 1, 2, 3, 6, 7, 14, 42 |
| б. 1, 2, 5, 7, 10, 14, 35, 70 |
| с. 1, 2, 7, 14 |
| д. 14 |
| д. 14 |
15.
| а. 1, 2, 4, 23, 46, 92 |
| б. 1, 5, 23, 115 |
| с. 1, 23 |
| д. 23 |
| д. 23 |
16.
| а. 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 |
| б. 1, 2, 3, 6, 9, 18, 27, 54 |
| с. 1, 3, 7, 9, 21, 63 |
| д. 1, 3 |
| д. 3 |
| ф. 3 |
17.
| а. 14 | б. 23 | с. 3 |
| д. 34 | е. 25 | ф. 42 |
18. а.\(24 \cdots 3 \cdots 132\)
19.
| а.\(2^{4} \cdots 3^{2} \cdots 7^{6} \cdots 13^{2}\) |
| б.\(3^{4} \cdots 5^{2}\) |
| c.\(a^{4} \cdots c^{3} \cdots d^{3} \cdots e^{2}\) |
| д.\(a^{2} \cdots d^{3}\) |
22. а. 2, 7
23. 1
24.
| а. м | б. 2м | куб. м |
| д. 1 | е. м |
25. а - г: 1, 2, 3, 6
h. однакові фактори
26. а - ф: 6
27.
| а. 13 | б. 18 | с. 36 |
28.
| а. 38 р. 186 |
| б. 9 р. 33 |
| с.7 р. 11 |
| д. 8 р. 25 |
29.
| а. 13 | б. 18 | с. 36 |
30. д. 22
31. д. 31
32. д. 1
34. 14|п якщо 2|н і 7|н.
35.
| а. правда з 2|742 і 7|742 |
| b. false —7 не є коефіцієнтом 968 |
| c False —2 не є коефіцієнтом 483 |
36. Подумайте, чому ви думаєте, що це не працює. На це питання можете відповісти тільки ви.
37. Подумайте, чому ви думаєте, що це працює. На це питання можете відповісти тільки ви.
38.
| а. 4|п і 3|н |
| б. 9|н і 2|н |
39.
| а. 35|п, якщо 5|п і 7|н |
| б. 28|п, якщо 4|п і 7|н |
| c. 75|п, якщо 3|п і 25|н |
| д. 56|п якщо 7|н і 8|н |
| е. з|н, якщо 4|п, 27|н, 25|н і 11|н |
| ф. д|п, якщо 16|п, 3|н, 5|п і 11|н |
40.
| а - е. 1 |
| f No; 1 - найменший коефіцієнт кожного числа. |
Набір вправ 3 Рішення
1.
| а. 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 |
| б. 12, 24, 36, 48, 60, 72, 84, 96, 108, 120 |
| с. 24, 48, 72 |
| д. 24 |
| е. ні |
2.
| а. 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60 |
| б. 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 66, 72, 78, 84, 90 |
| c. 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150 |
| д. 60 |
| е. 60 |
5.
| а. X, Y |
| б. Y, Z |
| c. х, Y |
7. \(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 11^{2} \cdots 1^{3}\)
8. \(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\)
9. \(2^{4} \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 1^{9} \cdots 23^{2}\)
10.
|
а. GCF:\(2^{2} \cdots 3^{2} \cdots 1^{3}\) НКМ:\(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 1^{3}\) |
|
б. ЗКФ: 2 НКМ:\(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\) |
|
c. ЗКФ:\(c^{3} \cdots d\) НКМ:\(a^{5} \cdots b^{4} \cdots c^{5} \cdots d^{3} \cdots e^{2}9\). |
|
d. ЗКФ:\(c \cdots d\) НКМ:\(a^{6} \cdots b^{4} \cdots c^{4} \cdots d^{3} \cdots e^{7}\) |
11.
| а. 120 |
| б. 1400 |
| в. 1274 |
| д. 840 |
| е. 1870 |
12.
| а. 3 · 2 · 2 · 7 · 3 · 5 = 1260 |
| б. 2·3·3·11·7·5·2·2·2·17 = 942 480 |
| в. 5·2·3·7·2·2·17·3·5 = 214 200 |
| д. 3 · 5 · 2 · 3 · 2 · 5 · 7 = 6300 |
13. 14 112
14. 2 835
15. 3 705
16. 2 і 20; 4 і 10
17.
| а. 21 | б. 18 018 |
18.
| а. 73 | б. 74 095 |
19.
| а. 37 | б. 395 641 |
20.
| а. 6 | б. 58 344 300 |
25.
| а. 2 (4n + 10) - парне число. |
| б. 2 (5к+ 4) + 1 - непарне число. |
| c. 5x+ 2 може бути парним або непарним |
26. Нехай 2n = одне парне число, і нехай 2m = ще одне парне число. Сума дорівнює: 2n+2m = 2 (n+m), що знаходиться у вигляді парного числа. Тому сума 2-х парних чисел парна.
27. Нехай 2n + 1 = одне непарне число, і нехай 2m + 1 = ще одне непарне число. Сума дорівнює: 2n + 1 + 2м + 1 = 2n + 2m + 2 = 2 (n + m + 1), що знаходиться у вигляді парного числа. Тому сума 2 непарних чисел парна
28. Нехай 2n = одне парне число, і нехай 2m + 1 = одне непарне число. Сума дорівнює: 2n + 2м + 1 = 2n + 2m + 1 = 2 (n + m) + 1, що знаходиться у вигляді непарного числа. Тому сума парного і непарного числа непарна.
29. Нехай 2n = одне парне число, і нехай 2m = ще одне парне число. Твір таке: 2n · 2m = 4mn = 2 (2mn), що знаходиться у вигляді парного числа. Тому добуток двох парних чисел парне.
30. Нехай 2n + 1 = одне непарне число, і нехай 2m + 1 = одне непарне число. Твір таке: (2n + 1) (2м +) = 2нм + 2n + 1 = 2 (нм + m + n) + 1, що знаходиться у вигляді непарного числа. Тому добуток двох непарних чисел непарне.
31. Нехай 2n = одне парне число, і нехай 2m + 1 = одне непарне число. Твір таке: 2n (2m + 1) = 4nm + 2n = 2 (2nm + n), що знаходиться у вигляді парного числа. Тому добуток парного числа і непарного числа парне.
32. 3240
33. 3240
34. 31 375
35.
| а. 3,77 |
| б.148, 181 |
| с.195,650 |
36.
| а. 3 775 |
| б. 148 181 |
| c. 195 650 |
| d. [n — (k —1)]\((n + k) \div 2\) або (n —k + 1)\((n + k) \div 2\) |
37. кратні 7
38. 1 + 2 + 3 +. + 99 + 100
39.
| а. 5 050 |
| б. 5 050 |
| c. 35 350 |
40.
| а. 63 000 |
| б. 41 151 |
| в. 226 500 |
41. кратні 4
42. 28 + 29 + 30 +. + 131 + 132
43. 33 600
44.
| а. 54 450 |
| б. 96 019 |
45. 6
46. 4, 8, 14
47. 4, 6
48. 4
49. 8
50. 3, 7
51. 7
52. 68, 178, 288, 398, 508, 618, 728, 838, 948
53. 5
54. 5
55. 5 або 26
56. мульт. з 7
57. 9 або 23
58. 3, 5, або 9
59. 9
60. Так; пояснення тут не надано
Рішення для домашніх завдань
1. ФУТ: 14; СМ: 6,300
3. а. ГКФ: 47; НКМ: 49 350
4. а Так як число парне, нам потрібно лише зробити отримане число ділимо на 3. Цифровий корінь поки що дорівнює 8. Отже, вирішіть, які одиничні цифри можна додати до 8, щоб отримати число, яке все ще ділиться на 3. Додавання 1, 4 або 7 до 8 буде працювати. Таким чином, можливості 4, 7 або 8.
5. Приклади і зустрічні приклади не наводяться цими рішеннями. Переконайтеся, що ви їх надаєте!
| a. помилковий |
| б. правда |
6.
| а.\(7 \cdots 53\) |
| д.\(7 \cdots 41\) |
7.
| а. м |
| б. м |
| куб. м |
| д. 1 |
9.
| в. 49 770 |
| б. 35 800 |
10.
| а. 39 |
| б. 80 |
11.
| а. 1, 2, 3; 6; ідеальний |
| б. 1; 1; дефіцитний |
| c. 1, 2, 4; 7; дефіцитний |
13. Приклади і контрприклади тут не наводяться. Переконайтеся, що ви їх надаєте.
| а. помилковий |
| б. правда |
| c. помилковий |
| d. правда |
15. а. 84
Модуль 9 Раціональні числа
Рішення для розігріву
1. Р
2. У
3. Р
4. D
5. O
6. D
7. Ч
8. Б
9. D
10. O
11. У
12. Б
13. Б
14. Л
Набір вправ 1 Рішення
1. \(\frac{1}{12} < \frac{1}{10} < \frac{1}{9} < \frac{1}{8} < \frac{1}{6} < \frac{1}{5} < \frac{1}{4} < \frac{1}{3} < \frac{1}{2}\)
2.
| а.\(\frac{1}{90}\) | б.\(\frac{1}{32}\) |
3. \(\frac{5}{12} < \frac{5}{10} < \frac{5}{9} < \frac{5}{8} < \frac{5}{6}\)
4.
| а.\(\frac{15}{37}\) | б.\(\frac{89}{100}\) |
5. \(\frac{4}{12} < \frac{4}{11} < \frac{4}{10} < \frac{4}{9} < \frac{4}{8} < \frac{4}{7} < \frac{4}{6} < \frac{4}{5}\)
6. Якщо ви порівнюєте два дроби, які мають однаковий чисельник, то більший показник має той, у якого менший знаменник.
7, 8. \(\frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{4}{5} < \frac{5}{6} < \frac{7}{8} < \frac{8}{9} < \frac{9}{10} < \frac{11}{12}\)
9.
| а.\(\frac{94}{95}\) | б.\(\frac{89}{100}\) |
10. \(\frac{13}{14} < \frac{25}{26} < \frac{34}{35} <\frac{45}{46} < \frac{51}{52} < \frac{71}{72} < \frac{99}{100}\)
11. Якщо порівнювати два дроби, де в кожному дробі чисельник на одиницю менше знаменника, то дріб з більшим чисельником і знаменником має більше значення.
12. Відповіді будуть відрізнятися. Спробуйте намалювати пиріг для кожної фракції, розтушовуючи в 2 з 3 рівних частин по 2/3 і 4 з 5 рівних частин по 4/5. Який пиріг більш затінений?
13. Відповіді будуть відрізнятися
14. \(\frac{2}{4}\)і\(\frac{3}{6}\) і\(\frac{4}{8}\) і\(\frac{5}{10}\) і\(\frac{6}{12}\)
15. \(\frac{4}{6}\)і\(\frac{6}{9}\) і\(\frac{8}{12}\)
16 - 17: Існує багато можливостей використання декількох смужок.
18. Помножте чисельник і знаменник на одне і те ж число, щоб отримати еквівалентний дріб.
19 - 27. Нижче наведені лише остаточні відповіді. Створіть власні моделі для вправ 22 - 28, слідуючи прикладам, переконавшись, що ви показуєте всі кроки, визначаєте одиниці, рядки, стовпці тощо.
19. \(\frac{3}{4} < \frac{4}{5}\)
20. \(\frac{13}{20}\)
21. \(\frac{5}{24}\)
22.
| а.\(\frac{8}{15}\) | б.\(\frac{15}{24}\) |
23.
| а.\(\frac{2}{3} \cdots \frac{5}{6} = \frac{10}{18}\) | б.\(\frac{1}{2} \cdots \frac{7}{8} = \frac{7}{16}\) |
24.
| а.\(\frac{4}{5} \cdots \frac{3}{5} = \frac{12}{25}\) | б.\(\frac{1}{7} \cdots \frac{3}{4} = \frac{3}{28}\) |
25. Відповіді можуть відрізнятися. Одна можливість: Нехай 1 = Н;\(\frac{3}{4}\) з Н = В;\(\frac{1}{3}\) з B = L;\(\frac{L}{H} = \frac{3}{12}\)
26.
| а. Н; В; Л; Л/Ч; 3/12 |
| б. н; Р; Ш; Вт/Н; 1/8 |
| с. н; Р; Л; Л/Н; 3/8 |
| д; Л; Р; Р/Д; 2/6 |
27 - 30. Зробіть власні моделі. Наводиться одна можливість для кожного використання моделі C-strip, але є й інші варіанти.
27. Нехай 1 одиниця = О, потім 1/10 = W і 1/5 = R Є 2 Вт в R, тому відповідь 2.
28. Нехай 1 одиниця = В, потім 1/9 = W і 1/3 = L. Є 3 W в L, тому відповідь 3.
29. Нехай 1 одиниця = Н, потім 1/6 = R і 2/3 = N. Є 4 R в N, тому відповідь 4.
30. Нехай 1 одиниця = P, потім 1/4 = W і 3 = H. Є 12 Вт в Н, тому відповідь 12.
31.
| a. еквівалент | б. еквівалент | c. не еквівалентний |
32. Можливостей нескінченно багато - ви можете використовувати кілька смужок, щоб знайти деякі.
33. Те ж саме, що і #31
34.
| а.\(\frac{14}{25}\) | б.\(\frac{13}{17}\) | c.\(\frac{18}{35}\) | д.\(\frac{15}{22}\) |
35. те саме, що і #31
36.
| а.\(\frac{4}{5} > \frac{5}{8}\) | б.\(\frac{12}{35} < \frac{11}{18}\) | c.\(\frac{13}{15} > \frac{14}{17}\) |
37. \(89 \cdots 95 < 90 \cdots 94\)починаючи з 8455 < 8460. Перехресні вироби перевіряють.
38. Це перевіряє, показує роботу
39.
| а. -4/70 | б. 71/72 |
40. Відповіді можуть відрізнятися. Деякі можливості: 21/50, 22/50, 23/50,., 29/50
41,42. 1/2
43. Деякі можливості: 51/150, 52/150, 53/150,., 59/150
44. Деякі можливості: 21/60, 22/60, 23/60,., 29/60
45. 241/300, 242/300, 243/300,., 249/300
46. 83/112
47. 75/112
48. Намалюйте 12 кіл. 11 кіл складіть до 66, тому покладіть по 6 в кожне коло. Відповідь: 6 учнів.
49. Намалюйте 7 кіл, так як 3 кола складіть до 36, покладіть по 12 в кожне коло. Інші 4 гуртки представляють студентів, які не купують обід. Відповідь: 48 студентів
50. Намалюйте 8 кіл. Оскільки всі 8 кіл складають до 120, покладіть по 15 в кожне коло. 5 кіл представляють самок, інші три представляють самців. Відповідь: 75 самок і 45 самців.
Набір вправ 2 Рішення
1.
| а. чотири десяті;\(\frac{4}{10} = \frac{2}{5}\) |
| б. двадцять шість сотих;\(\frac{26}{100} = \frac{13}{50}\) |
| c. три і вісім сотих\(3\frac{8}{100} = 3\frac{2}{25}\);\(\frac{388}{100} = \frac{77}{25}\) |
| d. дев'ять і вісімдесят п'ять сотих\(9\frac{85}{100} = 9\frac{17}{20}\);\(\frac{985}{100} = \frac{197}{20}\) |
| e. сімнадцять і триста п'ятитисячних\(17\frac{305}{1000}= 17\frac{61}{200}\);\(\frac{17305}{1000} = \frac{3461}{200}\) |
2.
| а. 0,14 | б. 008 |
| c. 4\(\frac{35}{100} = 4.35\) | д. 563\(\frac{8}{10} = 563.8\) |
| д. 3\(\frac{5}{100} = 3.05\) |
3.
| а. 0,028 | б. 0,32 |
| см. 0,075 | д. 0,66 |
4.
| а. 1,9; 1.90000 |
| б. 4.0340 |
5.
| а.3.5 > 9. |
| б. 35,06 = 3,0600 |
| c. 0,089 < 0,0908 |
6.
| а. 3,51 > 3,488 |
| б 35,061 < 35,35 |
| c. 0,8933 < 0,0894 |
7.
| а.\(2 \cdots 5\) | б.\(2 \cdots 5 \cdots 2 \cdots 5\) |
| c.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) | д.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
| е.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
8. 2 і 5
9. 3
10. 2
11. Ну, як ви думаєте?
12.
| а. 0,0875 | б. 0,875 |
13. Напишіть відповідь своїми словами.
14.
| а.\(\frac{3}{4} = \frac{3}{2 \cdots 2} \cdots \frac{5 \cdots 5}{5 \cdots 5} = \frac{75}{100} = 0.75\) |
| б.\(\frac{9}{20} = \frac{3 \cdots 3}{2 \cdots 2 \cdots 5} \cdots \frac{5}{5} = \frac{45}{100} = 0.45\) |
| c.\(\frac{9}{15} = \frac{3 \cdots 3}{3 \cdots 5} = \frac{3}{5} \cdots \frac{2}{2} = \frac{6}{10} = 0.6\) |
| д.\(\frac{18}{25} = \frac{2 \cdots 3 \cdots 3}{5 \cdots 5} \cdots \frac{2 \cdots 2}{2 \cdots 2} = \frac{72}{100} = 0.72}\) |
| e\(\frac{5}{14} = \frac{5}{2 \cdots 7}\) Це не може бути записано як кінцевий десятковий, оскільки зменшений коефіцієнт має простий множник 7 (який є відмінним від 2 або 5) у знаменнику. |
15. Зробіть три своїх.
16.
| а. 0, 1, 2, 3, 4, 5 |
| б. 0, 1, 2, 3, 4, 5, 6 |
| c. 0, 1, 2, 3, 4, 5, 6, 7, 8 |
| д. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 |
| е. 0, 1, 2 |
17. Зробіть три своїх.
18. а, б, д
19.
| а. є 33 (включаючи 0 як залишок). Максимум 32 цифри можуть бути в послідовності без повторення. |
| б Якщо ви робите довгий поділ, ви отримаєте 939393... |
| c. 2 |
| д. 13 і 31 |
20.
| а. 0. \(\bar{5}\)або 0,555... |
| б. 0. \(\bar{714285}\)або 0.714285714285... |
| c. 0,1\(\bar{6}\) або 0,1666... |
| д. 0. \(\bar{6}\)або 0,666.. |
| е. 0. \(\bar{63}\)або 0.636363... |
| ф. 0,41\(\bar{6}\) або 0,41666.. |
| г. 0,5\(\bar{3}\) або 0,5333... |
| ч. 0,3\(\bar{5}\) або 0,3555... |
| тобто 0,0\(\bar{75}\) або 0,0757575... |
21. х - 1
22.
10х = 7,272727... ;
100х = 72,727272... ;
1000 х = 727,272727...
23.
| а. 99x |
| б. 72 |
| в. 99х = 72; х =\(\frac{72}{99}\) |
| д. х =\(\frac{8}{11}\) |
24.
| а.\(\frac{4}{10} =\frac{2}{5}\) | б.\(\bar{4} = \frac{4}{9}\) |
| c.\(\frac{6}{100} = \frac{3}{50}\) | д.\(\bar{0.06} = \frac{6}{99} = \frac{2}{33}\) |
| е.\(\frac{9}{10}\) | f.\(\bar{0.9} = \frac{9}{9} = 1\) сюрприз! |
| г.\(\frac{45}{100} = \frac{9}{20}\) | ч. 0. \(\bar{45} = \frac{45}{99} = \frac{5}{11}\) |
| я.\(\frac{84}{1000} = \frac{21}{250}\) | Дж. 0. \(\bar{084} = \frac{84}{999} = \frac{28}{333}\) |
25.
| а.\(\frac{2.8}{99} = \frac{28}{99 \cdots 10} = \frac{14}{495}\) |
| б.\(\frac{2.6}{9} = \frac{26}{9 \cdots 10} = \frac{13}{45}\) |
| c.\(\frac{0.06}{9} = \frac{6}{9 \cdots 100} = \frac{1}{150}\) |
| д.\(\frac{101}{999}\) |
| е.\(\frac{3.6}{9} = \frac{36}{9 \cdots 10} = \frac{2}{5}\) |
26. Будьте креативними!
27. Ні, так як 9 - ідеальний квадрат. Отже,\(\sqrt{9} = 3\)
28-30. Будьте креативними!
31.
| a. раціональні (повторювані десяткові). |
| б. ірраціональний (має закономірність, але не повторюється!) |
| c. раціональний |
| d. ірраціональний (так як 80 не є ідеальним квадратом) |
| e. раціональний (так як 100 - ідеальний квадрат; так\(\sqrt{100} = 10\) |
| f. ірраціональний |
Рішення для домашніх завдань
1.
| а. К | c. д | е. д. | г Н |
2.
| а. ч | c. р | е. р |
3. а. л
7. \(\frac{1}{3} < \frac{3}{8}\)
8. \(\frac{17}{24}\)
9. \(\frac{7}{20}\)
10. а.\(\frac{3}{20}\)
11. а.\(\frac{5}{6} \cdots \frac{2}{3} = \frac{10}{18}\)
12. а.\(\frac{2}{3} \cdots \frac{3}{8} = \frac{6}{24}\)
13. а. Б; Г; Р; Р/Б; 2/9
14. а. 15
16. а.\(\frac{18}{35}\)
18. Деякі можливості: 31/80, 32/80, 33/80,., 49/80
20. а. намалюйте 10 кіл. Так як 7 кіл скласти до 21, покласти по 3 в кожне коло. Всі 10 гуртків складають до 30, тому є 30 учнів.
21.
| a. сім десятих |
| б. три і двадцять вісім сотих |
22.
| а.\(\frac{3}{10} \cdots \frac{8}{10} = \frac{14}{100} = 0.14\) |
| б.\(\frac{122}{100} \cdots \frac{23}{10} = \frac{2086}{1000} = 2.806\) |
23.
| а.\(\frac{11}{16} = \frac{11}{2 \cdots 2 \cdots 2 \cdots 2} \cdots \frac{5 \cdots 5 \cdots 5 \cdots 5}{5 \cdots 5 \cdots 5 \cdots 5} = \frac{6875}{10000} = 0.6875\) |
| c.\(\frac{1}{12} = \frac{1}{2 \cdots 2 \cdots 3}\) |
Це не може бути записано як кінцевий десятковий, оскільки зменшений коефіцієнт має простий множник 3 (який є відмінним від 2 або 5. у знаменнику).
24.
| а.\(\frac{7}{9}\) | c.\(\frac{235}{999}\) |