8.4.1: Ймовірність
- Page ID
- 67471
- Визначте подію, результат, випробування, просту подію та простір вибірки та обчислити ймовірність того, що подія відбудеться.
- Розрахуйте ймовірність подій для більш складних результатів.
- Вирішуйте програми, що включають ймовірності.
Вступ
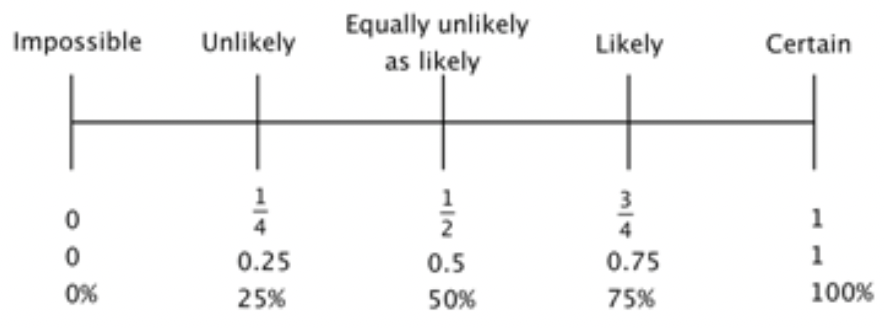
Імовірність забезпечує міру того, наскільки ймовірно, що щось станеться. Це число між числами і в тому числі і 1. Його можна записати як дріб, десятковий або відсоток.
Вибір номерів випадковим чином означає, що немає конкретного порядку, в якому вони обрані. Багато ігор використовують кістки або блешні для генерації чисел випадковим чином. Якщо ви розумієте, як розрахувати ймовірності, ви можете приймати продумані рішення про те, як грати в ці ігри, знаючи ймовірність різних результатів.
Визначення
Для початку потрібно знати деякі терміни, пов'язані з ймовірністю. При роботі з ймовірністю випадкове дію або ряд дій називають пробним. Результат - це результат судового розгляду, а подія - це конкретна сукупність результатів. Події зазвичай описуються з використанням загальної характеристики результатів.
Давайте застосуємо цю мову, щоб побачити, як ці терміни працюють на практиці. Деякі ігри вимагають прокатки плашки з шістьма сторонами, пронумерованими від 1 до 6. (Кубик - це множина померти.) Наведена нижче діаграма ілюструє використання тріалу, результату та події для такої гри:
| Пробний | Результати | Приклади подій |
| Прокатка плашки | Є 6 можливих результатів: {1, 2, 3, 4, 5, 6} |
Прокочування парного числа: {2, 4, 6} Прокатка 3: {3} Прокатка 1 або 3: {1, 3} Rolling a 1 і a 3: {} (Можна згорнути тільки одне число, тому такий результат неможливий. Подія не має результатів у ньому.) |
Зверніть увагу, що набір результатів ставиться в фігурні дужки і розділені комами.
Проста подія - це подія тільки з одним результатом. Прокатка 1 буде простою подією, тому що є лише один результат, який працює: 1! Прокатка більше 5 також буде простою подією, оскільки подія включає лише 6 як дійсний результат. Складна подія - це подія з більш ніж одним результатом. Наприклад, при прокатці однієї шестигранної матриці прокатка парного числа може відбуватися з одним з трьох результатів: 2, 4 і 6.
Коли ви катаєте шестигранну матрицю багато разів, ви не повинні очікувати, що будь-який результат буде відбуватися частіше, ніж інший (припускаючи, що це справедлива смерть). Результати в такій ситуації, як кажуть, однаково вірогідні. Дуже важливо визнати, коли результати однаково вірогідні при обчисленні ймовірності. Оскільки кожен результат у випробуванні штампування однаково вірогідний, ви очікуєте отримати кожен результат\(\ \frac{1}{6}\) рулонів. Тобто, ви\(\ \frac{1}{6}\) очікуєте, що рулони будуть 1,\(\ \frac{1}{6}\) з рулонів бути 2,\(\ \frac{1}{6}\) з рулонів, щоб бути 3, і так далі.
Вертушка ділиться на чотири рівні частини, кожна з яких забарвлена іншим кольором, як показано нижче. Коли цей прядильник закручується, стрілка вказує на один з кольорів. Чи однаково ймовірні результати?
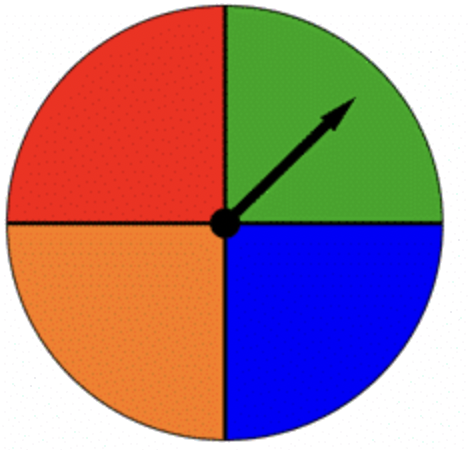
- Так, вони однаково вірогідні.
- Ні, вони не однаково ймовірні.
- Відповідь
- Всі результати однаково вірогідні. Кожен колір забезпечує різний результат, і кожен колір займає\(\ \frac{1}{4}\) коло. Ви очікуєте, що стрілка вкаже на кожен колір\(\ \frac{1}{4}\) часу.
Імовірність подій
Імовірність події полягає в тому, як часто вона повинна відбуватися. Вона являє собою відношення розмірів простору для проведення заходів до розміру вибіркового простору.
Для початку потрібно визначитися з розмірами місця для вибірки. Розмір простору вибірки - це загальна кількість можливих результатів. Наприклад, коли ви кидаєте 1 матрицю, простір зразка становить 1, 2, 3, 4, 5 або 6. Таким чином, розмір простору зразка дорівнює 6.
Потім потрібно визначитися з розмірами місця проведення заходів. Простір подій - це кількість результатів у заході, який вас цікавить. Простір подій для прокатки числа менше трьох дорівнює 1 або 2. Таким чином, розмір простору для заходів становить 2.
Для однаково ймовірних результатів ймовірність події Е може бути записана P (E).
\(\ P(E)=\frac{\text { size of the event space }}{\text { size of the sample space }}=\frac{\text { number of outcomes in the event }}{\text { total number of possible outcomes }}\)
Гра вимагає прокатки шестигранний штамп, пронумерований від 1 до 6. Яка ймовірність прокатки парного числа?
Рішення
|
\(\ \text { Sample space }=\{1,2,3,4,5,6\}\) \(\ \text { Event space }=\{2,4,6\}\) |
Спочатку знайдіть простір для зразків та простір подій. Простір вибірки - це всі можливі результати, а простір подій - результати події. У цьому випадку подія - «прокатка парного числа». |
| \(\ P(\text { even number })=P(\{2,4,6\})=\frac{3}{6}=\frac{1}{2}\) | Оскільки результати однаково вірогідні, ймовірність події є співвідношенням простору подій до простору вибірки. |
\(\ P(\text { even number })=\frac{1}{2}\)
Це звичайна практика з ймовірностями, як і з фракціями загалом, спростити ймовірність у найнижчі терміни, оскільки це полегшує більшості людей зрозуміти, наскільки вона велика. Якщо немає підстав не робити цього, висловлюйте всі остаточні ймовірності в найнижчих вираженнях.
Вертушка ділиться на рівні частини, кожна з яких пофарбована в інший колір, як показано нижче. Знайдіть ймовірність закрутки синього або зеленого кольору на цій спиннері:
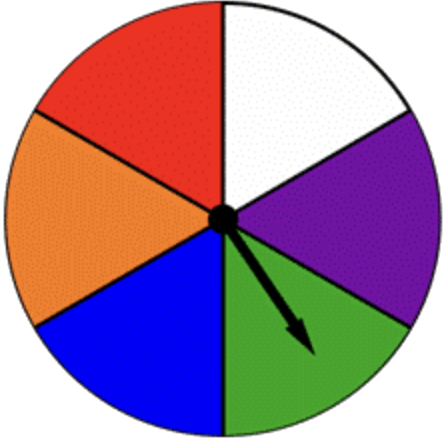
- \(\ \frac{1}{6}\)
- \(\ \frac{1}{3}\)
- 2
- 6
- Відповідь
-
- Неправильний. Є 6 однаково ймовірних результатів, тому ймовірність кожного результату є\(\ \frac{1}{6}\). Однак подія має два результати, {синій, зелений}. Імовірність є\(\ \frac{\text { size of event space }}{\text { size of sample space }}=\frac{2}{6}\). Правильна відповідь -\(\ \frac{1}{3}\).
- Правильно. Є 6 однаково ймовірних результатів, і подія має два результати, {синій, зелений}. Імовірність є\(\ \frac{\text { size of event space }}{\text { size of sample space }}=\frac{2}{6}=\frac{1}{3}\).
- Неправильний. Найбільше число, яке може бути значенням ймовірності - 1! У просторі подій є 2 результату, але ймовірність події - це відношення результатів у просторі подій до загальної кількості однаково ймовірних результатів. Є 6 однаково ймовірних результатів, тому ймовірність є\(\ \frac{\text { size of event space }}{\text { size of sample space }}=\frac{2}{6}=\frac{1}{3}\).
- Неправильний. Найбільше число, яке може бути значенням ймовірності - 1! У вибірковому просторі є 6 однаково ймовірних результатів, але ймовірність події - це відношення результатів у просторі подій до загальної кількості однаково ймовірних результатів. Імовірність є\(\ \frac{\text { size of event space }}{\text { size of sample space }}=\frac{2}{6}=\frac{1}{3}\).
Методи підрахунку для пошуку зразків просторів
Найскладнішим для обчислення ймовірності може бути знаходження розміру вибіркового простору, особливо якщо є два і більше випробувань. Існує кілька методів підрахунку, які можуть допомогти.
Перший, на який слід звернути увагу, - це складання діаграми. У наведеному нижче прикладі Торі перевертає дві монети. Тому потрібно ретельно визначитися з простором зразка. Діаграма, така як показана в наведеному нижче прикладі, є хорошим підходом.
Торі гортає пару монет і відзначає, скільки сальто «голів» вона отримує. Яка ймовірність того, що вона переверне 2 голови? Яка ймовірність того, що вона переверне всього 1 голову?
Рішення
|
Результати:
простір зразка: {HH, HT, TH, TT} простір для проведення заходів на 2 голів: {HH} простір для проведення заходу на 1 голову: {HT, TH} |
Створіть діаграму для запису результатів гортання першої монети, а потім результат перевертання другої монети. | |||||||||||||||
|
\(\ P(2 \text { heads })=P(\{\mathrm{HH}\})=\frac{1}{4}\) \(\ P(1 \text { head })=P(\{\mathrm{HT}, \mathrm{TH}\})=\frac{2}{4}=\frac{1}{2}\) |
Оскільки результати однаково вірогідні, ймовірність події є співвідношенням простору подій до простору вибірки. |
\(\ P(2 \text { heads })=\frac{1}{4}\)
\(\ P(1 \text { head })=\frac{1}{2}\)
У наведеному нижче прикладі простір зразка для Торі простий, оскільки котиться лише одна матриця. Однак, оскільки Джеймс котить дві матриці, діаграма допомагає організувати інформацію.
Торі прокотила шестигранну плашку і хотіла отримати результат або 1, або 4. Джеймс прокотив дві шестигранні кістки, один синій і один червоний, і хотів отримати результат як 1, так і 3, одночасно. Яка подія має більшу ймовірність?
Рішення
|
Простір зразків Торі: {1, 2, 3, 4, 5, 6} Івент-простір Торі: {1, 4} |
Спочатку знайдіть простір для зразків та простір подій для двох випробувань. Для судового розгляду Торі це просто. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\ \text { Tori: } P(1 \text { or } 4)=\frac{2}{6}=\frac{1}{3}\) | Оскільки результати однаково вірогідні, ймовірність події є співвідношенням простору подій до простору вибірки. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Це не так очевидно для суду Джеймса, оскільки він котить дві кістки. Він може створити і використовувати діаграму, щоб знайти можливості. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Простір вибірки Джеймса має 36 результатів. Івент-простір Джеймса має 2 результати. |
Є 36 результатів. З них є 2, які мають і 1, і 3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\ \text { James: } P(1 \text { and } 3)=\frac{2}{36}=\frac{1}{18}\) | Оскільки результати однаково вірогідні, ймовірність події є співвідношенням простору подій до простору вибірки. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подія Торі має більшу ймовірність.
Ви також можете використовувати деревоподібну діаграму для визначення простору зразка. Деревоподібна діаграма має гілку для кожного можливого результату для кожної події.
Припустимо, в шафі є три пари штанів (чорна, біла і зелена), чотири сорочки (зелена, біла, фіолетова і жовта) і дві пари взуття (чорна і біла). Скільки різних нарядів можна зробити? Є 3 варіанти штанів, 4 варіанти сорочок та 2 варіанти взуття. Для нашої діаграми дерева давайте використаємо B для чорного, W для білого, G для зеленого, P для фіолетового та Y для жовтого.
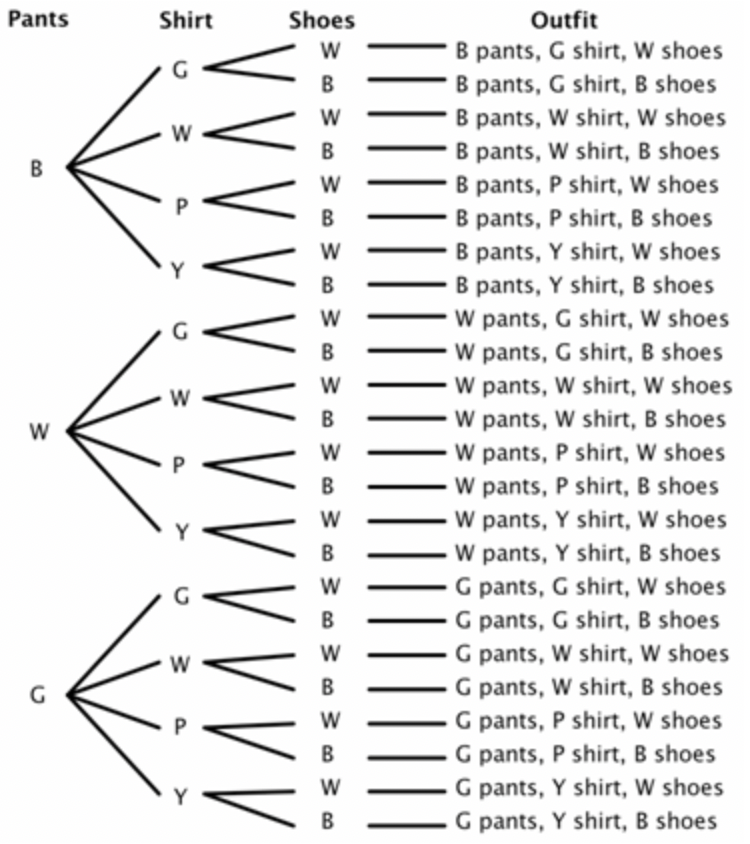
На діаграмі дерева видно, що в просторі зразків є 24 можливі наряди (деякі, можливо, не великий вибір).
Тепер ви могли б досить легко вирішити деякі проблеми ймовірності. Наприклад, яка ймовірність того, що якщо ви закриєте очі і вибираєте випадковим чином, ви б вибрали штани і взуття одного кольору? У графіку є 8 нарядів, де штани та взуття збігаються.
\(\ P(\text { same color })=\frac{8}{24}=\frac{1}{3}\)
Як ви бачили, коли судовий процес включає більше одного випадкового елемента, наприклад, гортання більше однієї монети або прокатки більше однієї матриці, вам не завжди потрібно ідентифікувати кожен результат у просторі вибірки, щоб обчислити ймовірність. Вам потрібно лише кількість результатів.
Основний принцип підрахунку - це спосіб знайти кількість результатів без перерахування та підрахунку кожного з них.
Якщо одна подія має\(\ p\) можливі результати, а інша подія має\(\ m\) можливі результати, то існує загальна кількість\(\ p \cdot m\) можливих результатів для двох подій.
Приклади
- Прокатка двох шестигранних кубиків: Кожна матриця має 6 однаково ймовірних результатів, тому простір\(\ 6 \cdot 6\) вибірки становить 36 однаково ймовірних результатів.
- Перегортання трьох монет: Кожна монета має 2 однаково ймовірні результати, тому простір вибірки становить\(\ 2 \cdot 2 \cdot 2\) або 8 однаково ймовірних результатів.
- Прокатка шестигранної матриці і перевертання монети: простір зразка є\(\ 6 \cdot 2\) або 12 однаково ймовірних результатів.
Таким чином, ви можете використовувати Основний принцип підрахунку, щоб дізнатися, скільки нарядів є в попередньому прикладі. Є 3 варіанти штанів, 4 варіанти сорочок та 2 варіанти взуття. Використовуючи фундаментальний принцип підрахунку, у вас є\(\ 4 \cdot 3 \cdot 2=24\) різні наряди.
Баррі волонтери на благодійній прогулянці, щоб зробити обіди для всіх інших волонтерів. У кожну сумку він кладе:
- один з двох бутербродів (арахісове масло і желе, або індичка і сир),
- один з трьох чіпсів (звичайні картопляні чіпси, печені картопляні чіпси або кукурудзяні чіпси),
- один шматочок фрукта (яблуко або апельсин).
Він забув відзначити те, що було в сумках. Припускаючи, що кожен вибір однаково вірогідний, яка ймовірність того, що мішок Тереза отримує тримає арахісове масло і желе бутерброд і яблуко?
Рішення
|
Розмір місця для вибірки: Помножте (кількість варіантів бутербродів) на (кількість варіантів чіпів) на (кількість варіантів фруктів) Це дає вам:\(\ 2 \cdot 3 \cdot 2=12\) |
По-перше, використовуйте Основний принцип підрахунку, щоб знайти розмір простору зразка. |
|
Розмір івент-простору: Помножте (кількість варіантів бутербродів у події) на (кількість варіантів чіпів у події) на (кількість варіантів фруктів у події) Це дає вам:\(\ 1 \cdot 3 \cdot 1=3\) |
Для івент-простору дотримуйтесь того ж принципу. При цьому є всього один бутерброд і один шматочок фруктів, але допустимий будь-який з трьох видів чіпсів. |
| \(\ P(\mathrm{~PB} \& \mathrm{~J} \text { and apple })=\frac{\text { size of event space }}{\text { size of sample space }}=\frac{3}{12}=\frac{1}{4}\) | Використовуйте співвідношення, щоб знайти ймовірність. |
Керрі перевертає чотири монети і підраховує кількість хвостів. Існує чотири способи отримати рівно один хвіст: HHHT, HHTH, HTH і THHH. Яка ймовірність того, що Керрі отримає рівно один хвіст?
- \(\ \frac{1}{16}\)
- \(\ \frac{1}{8}\)
- \(\ \frac{1}{4}\)
- \(\ \frac{1}{2}\)
- Відповідь
-
- Неправильний. Оскільки для кожної монети є два результати, з тих пір існує 16 можливих результатів\(\ 2 \cdot 2 \cdot 2 \cdot 2=16\). Однак у події є чотири результати, тому ймовірність є\(\ \frac{4}{16}\), або\(\ \frac{1}{4}\).
- Неправильний. Оскільки для кожної монети є два результати, з тих пір існує 16 можливих результатів\(\ 2 \cdot 2 \cdot 2 \cdot 2=16\). Є чотири результати в події, тому ймовірність є\(\ \frac{4}{16}\), або\(\ \frac{1}{4}\).
- Правильно. Оскільки для кожної монети є два результати, з тих пір існує 16 можливих результатів\(\ 2 \cdot 2 \cdot 2 \cdot 2=16\). Є чотири результати в події, тому ймовірність є\(\ \frac{4}{16}\), або\(\ \frac{1}{4}\).
- Неправильний. Є два результати для кожної монети, але є 4 монети. Це означає, що існує 16 можливих результатів з тих пір\(\ 2 \cdot 2 \cdot 2 \cdot 2=16\). Є чотири результати в події, тому ймовірність є\(\ \frac{4}{16}\), або\(\ \frac{1}{4}\).
Резюме
Ймовірність допомагає зрозуміти випадкові, непередбачувані ситуації, коли можливі кілька результатів. Це міра ймовірності події, і вона залежить від співвідношення події та можливих результатів, якщо всі ці результати однаково вірогідні.
\(\ P(E)=\frac{\text { size of the event space }}{\text { size of the sample space }}=\frac{\text { number of outcomes in the event }}{\text { total number of possible outcomes }}\)
Основний принцип підрахунку є ярликом для пошуку розміру простору вибірки, коли є багато випробувань і результатів:
Якщо одна подія має\(\ p\) можливі результати, а інша подія має\(\ m\) можливі результати, то існує загальна кількість\(\ p \cdot m\) можливих результатів для двох подій.
