3.1: Функції живлення

Last updated
Save as PDF

Page ID: 60043

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

З картону вирізається квадрат, причому кожна сторона має довжину$L$. Якщо ми хотіли написати функцію для площі квадрата, з$L$ як вхід і площа як вихід, ви можете згадати, що площу прямокутника можна знайти, помноживши довжину на ширину. Оскільки наша форма квадратна, довжина і ширина однакові, даючи формулу:

\[A(L)=L\cdot L=L^{2}\]

Так само, якщо ми хотіли функцію для об'єму куба з кожної сторони має певну довжину$L$, ви можете згадати об'єм прямокутної коробки можна знайти, помноживши довжину на ширину на висоту, які всі рівні для куба, даючи формулу:

\[V(L)=L\cdot L\cdot L=L^{3}\]

Ці дві функції є прикладами силових функцій, функцій, які є деякою мірою змінної.

Визначення: Функція живлення

Функція живлення - це функція, яка може бути представлена у вигляді

\[f(x)=x^{p}\]

Де базою є змінною, а показником$p$, є числом.

Приклад$\PageIndex{1}$

Які з функцій нашого інструментарію є силовими функціями? (Цей розділ є частиною Preculus: Дослідження функцій © Lippman & Rasmussen 2017, і містить вміст, ремікс з дозволу Алгебри коледжу © Stitz & Zager 2013. Цей матеріал ліцензується на умовах ліцензії Creative Commons CC-BY-SA.)

Рішення

Функції постійної та ідентичності є силовими функціями, оскільки їх можна записати як$f(x)=x^{0}$ і$f(x)=x^{1}$ відповідно.

Квадратичні і кубічні функції - це як степеневі функції з цілими числовими степенями:$f(x)=x^{2}$ і$f(x)=x^{3}$.

Взаємні та взаємні квадратні функції є обома силовими функціями з негативними повноваженнями цілого числа, оскільки вони можуть бути записані як$f(x)=x^{-1}$ і$f(x)=x^{-2}$.

Функції квадратного та кубового кореня є одночасно силовими функціями з дробовими степенями, оскільки вони можуть бути записані як$f(x) = x^{\dfrac{1}{2}}$ або$f(x) = x^{\dfrac{1}{3}}$

Вправа$\PageIndex{1}$

Який момент (и) мають спільні функції живлення інструментарію?

Відповідь: (0, 0) і (1, 1) є загальними для всіх силових функцій.

Характеристика силових функцій

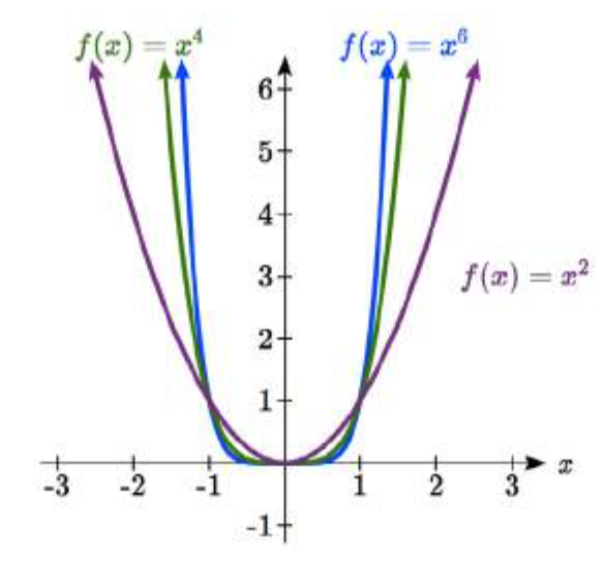$Графіки x ^ 2, x^4 та x^6, усі U-подібні та проходять через початок та 1 кома 1. x^6 є найплоснішим біля початку та найкрутішим від походження; x^2 є найбільш округлим біля початку та найменш крутим від походження.$ На малюнку праворуч наведені графіки$f(x)=x^{2}$, і$f(x)=x^{4}$$f(x)=x^{6}$, всі навіть цілі числові повноваження. Зверніть увагу, що всі ці графіки мають досить схожу форму, дуже схожу на квадратичний інструментарій, але зі збільшенням потужності графіки трохи згладжують біля початку і стають крутішими від початку.

Щоб описати поведінку, коли числа стають все більшими і більшими, ми використовуємо ідею нескінченності. Символ позитивної нескінченності є$\infty$, а$-\infty$ для негативної нескінченності. Коли ми говоримо, що «$x$наближається до нескінченності»$x \to \infty$, що символічно можна написати як, ми описуємо поведінку — ми говоримо,$x$ що стає великим в позитивному напрямку.

З парними функціями потужності, коли$x$ стає великим або в позитивному, або негативному напрямку, вихідні значення стають дуже великими додатними числами. Аналогічно, ми могли б описати це, кажучи, що$x$ наближаючись до позитивної або негативної нескінченності,$f(x)$ значення наближаються до позитивної нескінченності У символічній формі ми могли б написати: як$x \to \pm \infty$,$f(x) \to \infty$.

Тут наведені графіки$f(x)=x^{3}$, і$f(x)=x^{5}$$f(x)=x^{7}$, всі непарні цілі числові повноваження. Зверніть увагу, що всі ці графіки схожі на кубічний інструментарій, але знову ж таки, коли потужність збільшується, графіки згладжують біля початку і стають крутішими від початку.

$Графіки x ^ 3, x^5 та x^7, всі спочатку швидко зростають, сплющуються біля початку, потім знову збільшуються, проходячи через 1 кому 1. x^7 найплощіший біля початку та найкрутіший від походження; x ^ 3 є найбільш округлим біля початку та найменш крутим від початку.$

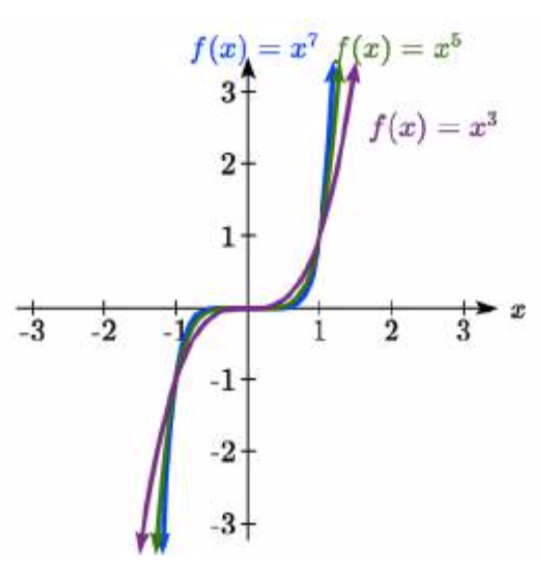
Для цих непарних степеневих функцій, як$x$ наближається до негативної нескінченності,$f(x)$ наближається У міру$x$ наближення позитивної нескінченності$f(x)$ наближається позитивна В символічній формі пишемо: як$x \to - \infty$,$f(x) \to - \infty$ і як$x \to \infty$,$f(x) \to \infty$.

Визначення: довгострокова поведінка

Поведінка графіка функції, оскільки вхідні дані набувають великих негативних значень$x \to - \infty$$x \to \infty$, і великих позитивних значень, називається довгостроковою поведінкою функції.

Приклад$\PageIndex{2}$

Опишіть довгострокову поведінку графіка$f(x)=x^{8}$.

Рішення

Оскільки$f(x)=x^{8}$ має цілу, рівну потужність, ми очікуємо, що ця функція буде вести себе дещо як квадратична функція. Оскільки вхід отримує великий позитивний або негативний, ми очікуємо, що вихід буде рости без обмежень у позитивному напрямку. У символічній формі, як$x \to \pm \infty$,$f(x) \to \infty$.

Приклад$\PageIndex{3}$

Опишіть довгострокову поведінку графіка$f(x)=-x^{9}$

Рішення

Оскільки ця функція має цілу непарну потужність, ми очікуємо, що вона буде вести себе дещо як кубічна функція. Негативний перед викличе вертикальне відображення, тому, як входи ростуть великими позитивними, виходи будуть рости великими в негативному напрямку, а оскільки входи ростуть великими негативними, виходи будуть рости великими в позитивному напрямку.$x^{9}$ У символічній формі для довгострокової поведінки ми б писали: як$x \to \infty$,$f(x)\to - \infty$ і як$x\to - \infty$,$f(x) \to \infty$.

Ви можете використовувати слова або символи для опису довгострокової поведінки цих функцій.

Вправа$\PageIndex{2}$

Опишіть словами та символами довгострокову поведінку$f(x)=-x^{4}$

Відповідь: Як$x$ наближається позитивна і негативна нескінченність,$f(x)$ наближається негативна нескінченність: як$x \to \pm \infty$,$f(x) \to -\infty$ через вертикального перевертання

Лікування раціональних і радикальних форм силових функцій буде збережено на потім.

Поліноми

Нафтопровід лопається в Мексиканській затоці, викликаючи нафтову пляму приблизно круглої форми. В даний час пляма в радіусі 24 миль, але цей радіус збільшується на 8 миль щотижня. Якби ми хотіли написати формулу для області, покритої масляною плямою, ми могли б зробити це, склавши дві функції разом. Перший являє собою формулу радіуса$r$, розливу, який залежить від кількості тижнів, w, що пройшли.

Сподіваємось, ви визнали, що цей зв'язок є лінійним:

\[r(w)=24+8w\nonumber\]

Ми можемо поєднати це з формулою для площі кола:$A$

\[A(r)=\pi r^{2}\nonumber \]

Складання цих функцій дає формулу для області в терміні тижнів:

\[A(w)=A(r(w))=A(24+8w)=\pi (24+8w)^{2}\nonumber \]

Множення цього з дає формулу

\[A(w)=576\pi +384\pi w+64\pi w^{2}\nonumber \]

Ця формула є прикладом многочлена. Многочлен - це просто сума членів, кожен з яких складається з вертикально розтягнутої або стисненої силової функції з невід'ємною цілою числовою силою.

термінологія поліноміальних функцій

Многочлен - це функція, яку можна записати як

\[f(x)=a_{0} +a_{1} x+a_{2} x^{2} +\cdots +a_{n} x^{n} \label{poly1}\]

Кожна з$a_{i}$ констант називається коефіцієнтами і може бути додатною, від'ємною або нульовою, і бути цілими числами, десятковими числами або дробами.
Член многочлена - це будь-яка одна частина суми, тобто будь-яка$a_{i} x^{i}$. Кожен окремий термін - це перетворена силова функція.
Ступінь многочлена - це найвища сила змінної, яка зустрічається в многочлені.
Провідним терміном є термін, що містить найвищу силу змінної: термін з найвищим ступенем.
Провідний коефіцієнт - коефіцієнт провідного члена.

Через визначення «провідного» терміна ми часто переставляємо Equation\ ref {poly1} так, щоб степені були спадними.

\[f(x)=a_{n} x^{n} +.....+a_{2} x^{2} +a_{1} x+a_{0} \label{poly2}\]

Приклад$\PageIndex{4}$

Визначте ступінь, провідний термін та провідний коефіцієнт цих многочленів:

$f(x)=3+2x^{2} -4x^{3}$
$g(t)=5t^{5} -2t^{3} +7t$
$h(p)=6p-p^{3} -2$

Рішення

Для функції$f(x)$ ступінь дорівнює 3, найвища потужність включена$x$. Провідним терміном є термін, що містить цю владу,$-4x^{3}$. Провідним коефіцієнтом є коефіцієнт цього терміну, -4.
Бо$g(t)$, ступінь дорівнює 5, провідний термін -$5t^{5}$, а провідний коефіцієнт - 5.
Бо$h(p)$, ступінь дорівнює 3, провідний член - це$-p^{3}$, тому провідний коефіцієнт дорівнює -1.

Означення: довгострокова поведінка многочленів

Для будь-якого полінома довгострокова поведінка многочлена буде відповідати довгостроковій поведінці провідного члена.

Приклад$\PageIndex{5}$

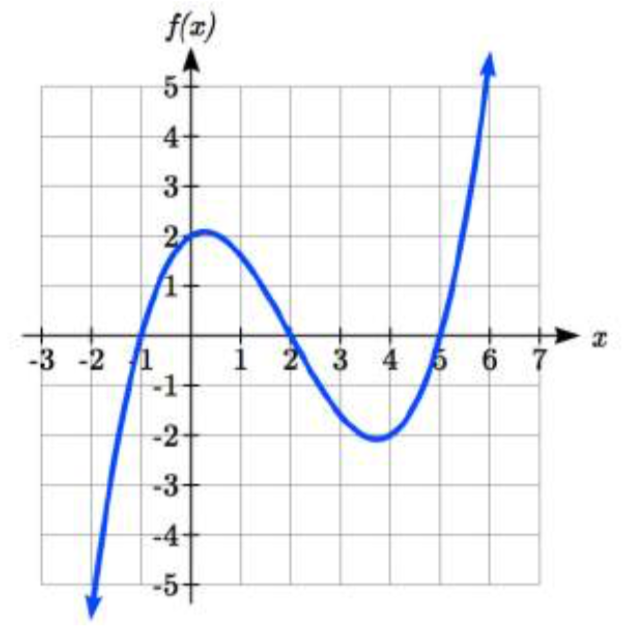
Що ми можемо визначити про довгострокову поведінку та ступінь рівняння для полінома, зображеного тут?

$Поліноміальний графік збільшується до 0 кома 2, зменшується приблизно до 3,8 коми негативного 2.1, потім збільшується.$

Рішення

Оскільки вихід зростає великим і позитивним, оскільки входи стають великими та позитивними, ми описуємо довгострокову поведінку символічно, написавши: as$x \to \infty$,$f(x) \to \infty$. Аналогічно, як$x \to -\infty$,$f(x) \to -\infty$.

Словом можна сказати, що коли значення наближаються до нескінченності,$x$ значення функції наближаються до нескінченності, а коли$x$ значення наближаються до негативної нескінченності, значення функції наближаються до негатив

Ми можемо сказати, що цей графік має форму непарної степеневої функції, яка не була відображена, тому ступінь полінома, що створює цей графік, повинна бути непарною, а провідний коефіцієнт буде позитивним.

Вправа$\PageIndex{3}$

Враховуючи функцію,$f(x)=0.2(x-2)(x+1)(x-5)$ використовуйте свої навички алгебри, щоб записати функцію у стандартній поліноміальній формі (як суму членів) та визначити провідний член, ступінь та довгострокову поведінку функції.

Відповідь: Провідним терміном є$0.2x^{3}$, так це поліном 3 ступеня. Як наближається нескінченність (або стає дуже великим в позитивному напрямку)$x$ наближається$f(x)$ до нескінченності; як$x$ наближається негативна нескінченність (або стає дуже великою в негативному напрямку)$f(x)$ наближається до негативної нескінченності. (В основному довгострокова поведінка така ж, як і кубічна функція).

Короткострокова поведінка

Характеристики графіка, такі як вертикальні та горизонтальні перехоплення та місця, де графік змінює напрямок, є частиною короткочасної поведінки полінома.

Як і у всіх функціях, вертикальний перехоплення - це місце, де графік перетинає вертикальну вісь, і відбувається, коли вхідне значення дорівнює нулю. Оскільки многочлен - це функція, то може бути тільки один вертикальний перехоплення, який відбувається в точці$(0, a_{0})$. Горизонтальні перехоплення відбуваються при вхідних значеннях, які відповідають вихідному значенню нулю. Можна мати більше одного горизонтального перехоплення.

Горизонтальні перехоплення також називають нулями, або коренями функції.

Приклад$\PageIndex{6}$

З огляду на поліноміальну функцію$f(x)=(x-2)(x+1)(x-4)$, написану в факторованому вигляді для вашої зручності, визначте вертикальний і горизонтальний перехоплення.

Рішення

Вертикальний перехоплення відбувається, коли вхід дорівнює нулю.

\[f(0)=(0-2)(0+1)(0-4)=8\nonumber \]

Графік перетинає вертикальну вісь у точці (0, 8).

Горизонтальні перехоплення відбуваються, коли на виході дорівнює нулю.

\[0=(x-2)(x+1)(x-4)\nonumber \]коли$x$ = 2, -1, або 4.

$f(x)$має нулі, або коріння, при$x$ = 2, -1 і 4.

Графік перетинає горизонтальну вісь у точках (2, 0), (-1, 0) та (4, 0)

Зауважте, що многочлен у попередньому прикладі, який би мав ступінь три, якщо помножити, мав три горизонтальні перехоплення та дві поворотні точки - місця, де графік змінює напрямок. Зараз ми зробимо загальну заяву, не обґрунтувавши це — причини стануть зрозумілі далі в цьому розділі.

перехоплення і поворотні точки многочленів

Многочлен ступеня$n$ матиме:

Максимально$n$ горизонтальні перехоплення. Поліном непарного ступеня завжди буде принаймні один.
У більшості$n - 1$ поворотних моментів

Приклад$\PageIndex{7}$

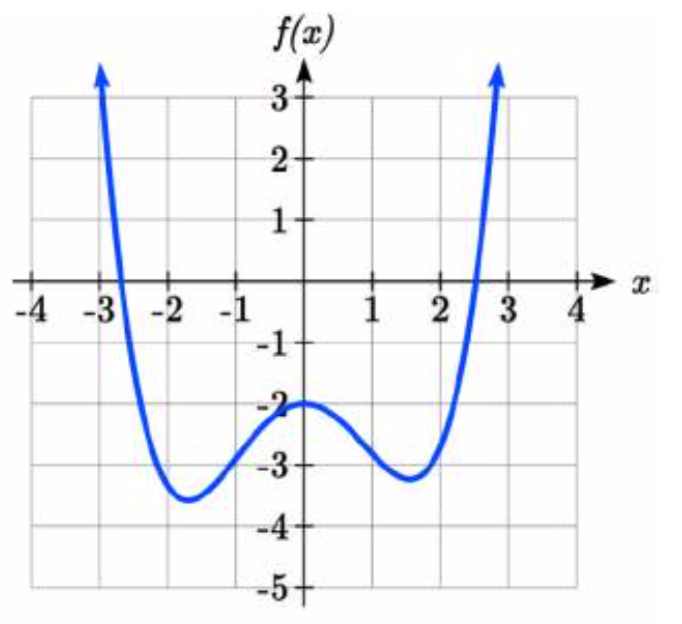
Що можна зробити висновок про графіку многочлена, показаного тут?

$Поліноміальний граф зменшується приблизно до (від'ємний 1,7, від'ємний 3,5), збільшується до 0 кома негативний 2, зменшується до 1.6 кома негативний 3,2, потім збільшується.$

Рішення

Виходячи з довгострокової поведінки, коли графік стає великим позитивним на обох кінцях графіка, ми можемо визначити, що це графік полінома парного ступеня. Графік має 2 горизонтальних перехоплення, що припускають ступінь 2 або більше, і 3 точки повороту, що передбачає ступінь 4 або більше. Виходячи з цього, було б розумно зробити висновок, що ступінь рівна і принаймні 4, тому це, ймовірно, поліном четвертого ступеня.

Вправа$\PageIndex{4}$

З огляду на функцію$f(x) = 0.2(x-2)(x+1)(x-5)$, визначте поведінку короткого пробігу.

Відповідь: Горизонтальні перехоплення - це (2, 0) (-1, 0) і (5, 0), вертикальний перехоплення - (0, 2) і на графіку є 2 повороти.

Важливі теми цього розділу

Функції живлення
Поліноми
коефіцієнти
провідний коефіцієнт
Термін
Провідний термін
Ступінь многочлена
Довготривала поведінка
Короткострокова поведінка