36.6: Абсолютне значення чисел

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Урок

Давайте вивчимо відстані від нуля ближче.

Вправа $\PageIndex{1}$ : Number Talk: Closer to Zero

Для кожної пари виразів подумки визначте, який з них має значення, яке ближче до 0.

$\frac{9}{11}$ або $\frac{15}{11}$

$\frac{1}{5}$ або $\frac{1}{9}$

$1.25$ або $\frac{5}{4}$

$0.01$ або $0.001$

Вправа $\PageIndex{2}$ : Jumping Flea

Перемістіть помилку в початкову точку, виберіть відстань стрибка і натисніть кнопку стрибка. Можливо, вам доведеться збільшити або зменшити масштаб, якщо ваша помилка вискакує з екрану.

Помилка стрибає навколо на числовому рядку.
1. Якщо помилка починається з 1 і стрибає 4 одиниці вправо, де це в кінцевому підсумку? Як далеко від 0 це?
2. Якщо помилка починається з 1 і стрибає на 4 одиниці вліво, де це в кінцевому підсумку? Як далеко від 0 це?
3. Якщо помилка починається з 0 і стрибає 3 одиниці, де він може приземлитися?
4. Якщо помилка стрибає 7 одиниць і приземлиться на 0, де він міг би розпочатися?
5. Абсолютне значення числа - це відстань, яке воно становить від 0. На даний момент помилка знаходиться ліворуч від 0, а абсолютне значення його розташування дорівнює 4. Де на числовому рядку вона?
6. Якщо помилка знаходиться зліва від 0 і абсолютне значення його розташування дорівнює 5, де на числовому рядку він знаходиться?
7. Якщо помилка знаходиться праворуч від 0 і абсолютне значення його розташування дорівнює 2,5, то де на числовому рядку він знаходиться?
Ми використовуємо позначення, $|-2|$ щоб сказати «абсолютне значення -2», що означає «відстань -2 від 0 на числовій лінії».
1. Що $|-7|$ означає і в чому його цінність?
2. Що $|-1.8|$ означає і в чому його цінність?

Вправа $\PageIndex{3}$ : Absolute Elevation and Temperature

Частина міста Новий Орлеан знаходиться на 6 футах нижче рівня моря. Ми можемо використовувати «-6 футів» для опису його висоти, а « $|-6|$ ноги» для опису його вертикальної відстані від рівня моря. Що б описувало кожне з наступних чисел у контексті висоти?
1. $25$ ноги
2. $|25|$ ноги
3. $-8$ ноги
4. $|-8|$ ноги
Висота міста відрізняється від рівня моря на 10 футів. Назвіть дві височини, які могло б мати місто.
Ми пишемо « $-5^{\circ}\text{C}$ », щоб описати температуру, яка на $5$ градусах Цельсія нижче температури замерзання і « $6^{\circ}\text{C}$ » для температури, яка на $5$ градуси вище замерзання. У цьому контексті, що описує кожне з наступних чисел?
1. $1^{\circ}\text{C}$
2. $-4^{\circ}\text{C}$
3. $|12|^{\circ}\text{C}$
4. $|-7|^{\circ}\text{C}$
1. Яка температура холодніше: $-6^{\circ}\text{C}$ або $3^{\circ}\text{C}$ ?
2. Яка температура ближче до температури замерзання: $-6^{\circ}\text{C}$ або $3^{\circ}\text{C}$ ?
3. Яка температура має меншу абсолютну величину? Поясніть, як ви знаєте.
Ви готові до більшого?

Резюме

Порівнюємо числа, порівнюючи їх позиції на числовому рядку: більше одне, що далі праворуч, менше.

Іноді ми хочемо порівняти, який з них ближче або далі від 0. Наприклад, ми можемо захотіти знати, наскільки далеко знаходиться температура від точки замерзання $0^{\circ}\text{C}$ , незалежно від того, вище або нижче замерзання.

Абсолютне значення числа говорить нам про його відстань від 0.

Абсолютне значення -4 дорівнює 4, тому що -4 дорівнює 4 одиницям зліва від 0. Абсолютне значення 4 також дорівнює 4, тому що 4 - це 4 одиниці праворуч від 0. Протилежності завжди мають однакове абсолютне значення, оскільки вони обидва мають однакову відстань від 0.

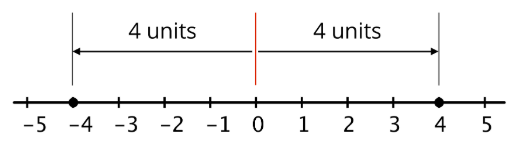
Відстань від 0 до самого себе дорівнює 0, тому абсолютне значення 0 дорівнює 0. Нуль - єдине число, відстань якого до 0 дорівнює 0. Для всіх інших абсолютних значень завжди є два числа - одне позитивне і одне негативне - які мають таку відстань від 0.

Щоб сказати «абсолютне значення 4», пишемо: $|4|$

Щоб сказати, що «абсолютне значення -8 дорівнює 8», пишемо: $|-8|=|8|$

Записи глосарію

Визначення: Абсолютне значення

Абсолютне значення числа - це його відстань від 0 на числовому рядку.

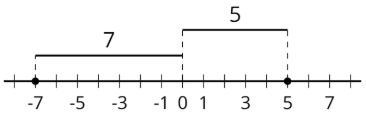
Абсолютне значення -7 дорівнює 7, тому що воно знаходиться на відстані 7 одиниць від 0. Абсолютне значення 5 дорівнює 5, тому що воно знаходиться на відстані 5 одиниць від 0.

Визначення: Від'ємне число

Від'ємне число - це число, яке менше нуля. На горизонтальному числовому рядку від'ємні числа зазвичай відображаються ліворуч від 0.

Визначення: Протилежне

Два числа протилежні, якщо вони знаходяться на однаковій відстані від 0 і по різні боки числової лінії.

Наприклад, 4 - протилежність -4, а -4 - протилежність 4. Вони обидва мають однакову відстань від 0. Один негативний, а інший - позитивний.

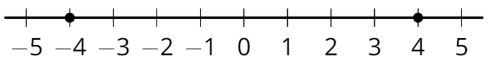
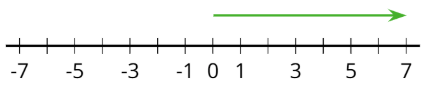
Визначення: Позитивне число

Позитивне число - це число, яке більше нуля. На горизонтальній числовій лінії позитивні числа зазвичай відображаються праворуч від 0.

Визначення: Раціональне число

Раціональне число - це дріб або протилежне дробу.

Наприклад, 8 і -8 є раціональними числами, оскільки їх можна записати як $\frac{8}{1}$ і $-\frac{8}{1}$ .

Крім того, 0,75 і -0,75 є раціональними числами, оскільки їх можна записати як $\frac{75}{100}$ і $-\frac{75}{100}$ .

Визначення: Знак

Знак будь-якого числа, відмінного від 0, є позитивним або негативним.

Наприклад, знак 6 позитивний. Знак -6 негативний. Нуль не має знака, тому що він не є позитивним або негативним.

Практика

Вправа $\PageIndex{4}$

На числовому рядку намітити і позначити всі числа з абсолютним значенням $\frac{3}{2}$ .

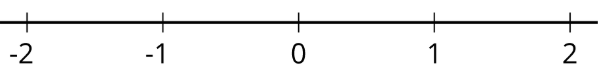
Вправа $\PageIndex{5}$

Температура на світанку знаходиться $6^{\circ}\text{C}$ далеко від 0. Виберіть всі температури, які можливі.

$-12^{\circ}\text{C}$
$-6^{\circ}\text{C}$
$0^{\circ}\text{C}$
$6^{\circ}\text{C}$
$12^{\circ}\text{C}$

Вправа $\PageIndex{6}$

Поставте ці цифри по порядку, від найменшого до найбільшого.

$|-2.7|\qquad 0\qquad 1.3\qquad |-1|\qquad 2$

Вправа $\PageIndex{7}$

Сім'я Ліна повинна проїхати 325 миль, щоб дістатися до будинку бабусі.

На 26 милі, який відсоток відстані поїздки вони пройшли?
Як далеко вони подорожували, коли пройшли 72% відстані поїздки?
На 377 миль, який відсоток відстані поїздки вони пройшли?

(Від блоку 5.4.3)

Вправа $\PageIndex{8}$

Олена жертвує гроші на благодійність щоразу, коли заробляє гроші нянею. У таблиці показано, скільки грошей $d$ , які вона жертвує на різні суми грошей $m$ , що заробляє.

Таблиця $\PageIndex{1}$
$d$	$4.44$	$1.80$	$3.12$	$3.60$	$2.16$
$m$	$37$	$15$	$26$	$30$	$18$

Який відсоток свого доходу Олена жертвує на благодійність? Поясніть або покажіть свою роботу.
Яка кількість, $m$ або $d$ , буде кращим вибором для залежної змінної в рівнянні, що описує зв'язок між $m$ і $d$ ? Поясніть свої міркування.
Використовуйте свій вибір з другого питання, щоб написати рівняння, яке стосується $m$ і $d$ .

(З блоку 6.4.1)

Вправа $\PageIndex{9}$

У скільки разів більше перше число в парі, ніж друге?

$3^{4}$ в _____ разів більше, ніж $3^{3}$ .
$5^{3}$ в _____ разів більше, ніж $5^{2}$ .
$7^{10}$ в _____ разів більше, ніж $7^{8}$ .
$17^{6}$ в _____ разів більше, ніж $17^{4}$ .
$5^{10}$ в _____ разів більше, ніж $5^{4}$ .

(Від блоку 6.3.1)