Skip to main content
LibreTexts - Ukrayinska

36.5: Використання негативних чисел для розуміння контекстів

  1. Last updated
  2. Save as PDF
  • Page ID
    870

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Урок

    Давайте розберемося з негативними сумами грошей.

    Вправа\(\PageIndex{1}\): Notice and Wonder: It Comes and Goes

    діяльність сума
    займатися моїми справами \(30.00\)
    нянька мого двоюрідного брата \(45.00\)
    купити мій обід \(-10.80\)
    отримати мою допомогу \(15.00\)
    купити сорочку \(-18.69\)
    домашня тварина моя собака \(0.00\)
    Таблиця\(\PageIndex{1}\)

    Що ви помічаєте? Що вам цікаво?

    Вправа\(\PageIndex{2}\): The Concession Stand

    Менеджер концесійного стенду веде облік всіх поставок, які вона купує, і всі предмети, які вона продає. У таблиці наведені деякі її записи за вівторок.

    пункт кількість вартість в доларах
    пончики \(-58\) \(37.70\)
    соломкою \(3,000\) \(-10.35\)
    хот-доги \(-39\) \(48.75\)
    піца \(13\) \(-116.87\)
    яблука \(-40\) \(14.00\)
    картопля фрі \(-88\) \(132.00\)
    Таблиця\(\PageIndex{2}\)
    1. Які предмети вона продавала? Поясніть свої міркування.
    2. Як ми можемо інтерпретувати -58 в цій ситуації?
    3. Як ми можемо інтерпретувати -10.35 в цій ситуації?
    4. На який предмет вона витратила найбільше грошей? Поясніть свої міркування.

    Вправа\(\PageIndex{3}\): Drinks for Sale

    Торговий автомат в офісній будівлі продає бутильовані напої. Машина відстежує всі зміни кількості пляшок від продажу та від заправки та технічного обслуговування машин. Цей запис показує зміни за кожні 5-хвилинний період протягом однієї години.

    1. Що може означати позитивне число в цьому контексті? А як щодо негативного числа?
    2. Що означало б «0» у другому стовпці в цьому контексті?
    3. Які цифри - позитивні чи негативні - призводять до меншої кількості пляшок у машині?
    4. В який час відбулася найбільша зміна кількості пляшок в машині? Як ця зміна вплинула на кількість пляшок, що залишилися в машині?
    5. У який період часу, 8:05 - 8:09 або 8:25 - 8:29, чи була більша зміна кількості пляшок у машині? Поясніть свої міркування.
    6. Машина повинна бути спорожнена для обслуговування. Якщо в автоматі є 40 пляшок, коли він буде обслуговуватися, який номер піде в другій колонці таблиці?
    час кількість пляшок
    8:00-8:04 \(-1\)
    8:05-8:09 \(+12\)
    8:10-8:14 \(-4\)
    8:15-8:19 \(-1\)
    8:20-8:24 \(-5\)
    8:25-8:29 \(-12\)
    8:30-8:34 \(-2\)
    8:35-8:39 \(0\)
    8:40-8:44 \(0\)
    8:45-8:49 \(-6\)
    8:50-8:54 \(+24\)
    8:55-8:59 \(0\)
    послуга
    Таблиця\(\PageIndex{3}\)

    Ви готові до більшого?

    Прия, Май, Лін пішли в кафе на вихідних. Їх спільний рахунок дійшов до 25 доларів. Кожен студент віддав серверу $10 купюру. Сервер взяв ці $30 і повернув п'ять $1 купюр в зміні. Кожен студент взяв $1 назад, залишивши решту, $2, як чайові для сервера.

    Коли вона йшла з кафе, Лін подумала: «Зачекайте - це не має сенсу. Так як я поклав $10 і отримав $1 назад, я заплатив $9. Так зробили Май і Прия. Разом ми заплатили 27 доларів. Тоді ми залишили підказку за 2 долари. Це складає $29 всього. І все ж ми спочатку віддали офіціантові 30 доларів. Куди пішов зайвий долар?»

    Подумайте про ситуацію і про питання Ліна. Чи згодні ви, що цифри не склалися належним чином? Поясніть свої міркування.

    Резюме

    Іноді ми представляємо зміни в величині з позитивними і негативними числами. Якщо кількість збільшується, зміна позитивна. Якщо вона зменшується, зміна негативна.

    • Припустимо, 5 галонів води покладено в пральну машину. Ми можемо уявити зміну кількості галонів як +5. Якщо 3 галони спорожняться з машини, ми можемо уявити зміну як -3.

    Особливо часто представляють гроші, які ми отримуємо з позитивними числами, і гроші, які ми витрачаємо з негативними числами.

    • Припустимо, Клер отримує $30.00 на день народження і витрачає $18.00, купуючи обід для себе і друга. До неї вартість подарунка може бути представлена як +30.00, а вартість обіду як -18.00.

    Чи вважається число позитивним чи негативним, залежить від точки зору людини. Якщо бабуся Клер дасть їй 20 доларів на день народження, Клер може побачити це як +20, тому що для неї сума грошей, яку вона збільшила. Але її бабуся може сприймати це як -20, тому що для неї кількість грошей у неї зменшилася.

    Загалом, використовуючи позитивні та негативні числа для представлення змін, ми повинні чітко розуміти, що це означає, коли зміна є позитивною, і що це означає, коли зміна негативна.

    Записи глосарію

    Визначення: Від'ємне число

    Від'ємне число - це число, яке менше нуля. На горизонтальному числовому рядку від'ємні числа зазвичай відображаються ліворуч від 0.

    clipboard_eb55c3d5de5b580d54a7fdadcb43eebe5.png
    Малюнок\(\PageIndex{1}\)

    Визначення: Протилежне

    Два числа є протилежними, якщо вони знаходяться на однаковій відстані від 0 і по різні боки числової лінії.

    Наприклад, 4 - протилежність -4, а -4 - протилежність 4. Вони обидва мають однакову відстань від 0. Один негативний, а інший - позитивний.

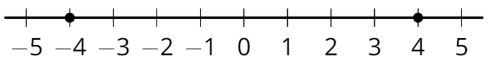
    clipboard_eda25bb95e8100e59945ae726bce85652.png
    Малюнок\(\PageIndex{2}\)

    Визначення: Позитивне число

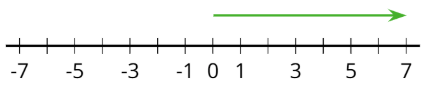
    Позитивне число - це число, яке більше нуля. На горизонтальній числовій лінії позитивні числа зазвичай відображаються праворуч від 0.

    clipboard_e57349099b60f3c066321203397a05ac8.png
    Малюнок\(\PageIndex{3}\)

    Визначення: Раціональне число

    Раціональне число - це дріб або протилежне дробу.

    Наприклад, 8 і -8 є раціональними числами, оскільки їх можна записати як\(\frac{8}{1}\) і\(-\frac{8}{1}\).

    Крім того, 0,75 і -0,75 є раціональними числами, оскільки їх можна записати як\(\frac{75}{100}\) і\(-\frac{75}{100}\).

    Визначення: Знак

    Знак будь-якого числа, відмінного від 0, є позитивним або негативним.

    Наприклад, знак 6 позитивний. Знак -6 негативний. Нуль не має знака, тому що він не є позитивним або негативним.

    Практика

    Вправа\(\PageIndex{4}\)

    Напишіть позитивне або негативне число, щоб представляти кожну зміну високої температури.

    1. Висока температура у вівторок була на 4 градуси менше, ніж висока температура понеділка.
    2. Висока температура в середу була на 3,5 градуса менше, ніж висока температура у вівторок.
    3. Висока температура в четвер була на 6,5 градусів більше, ніж висока температура в середу.
    4. Висока температура п'ятниці була на 2 градуси менше, ніж висока температура четверга.

    Вправа\(\PageIndex{5}\)

    Вирішіть, яка з наступних величин може бути представлена додатним числом, а яка може бути представлена від'ємним числом. Наведіть приклад величини з протилежним знаком в тій же ситуації.

    1. Щеня Тайлера набрав 5 фунтів.
    2. В акваріум просочилися 2 галони води.
    3. Андре отримав подарунок у розмірі 10 доларів.
    4. Кіран подарував в подарунок 10 доларів.
    5. Альпініст спустився на 550 футів.

    Вправа\(\PageIndex{6}\)

    Складіть ситуацію, коли змінюється кількість.

    1. Поясніть, що означає мати негативні зміни.
    2. Поясніть, що означає мати позитивні зміни.
    3. Наведемо приклад кожного.

    Вправа\(\PageIndex{7}\)

    1. На цифровій лінії позначте точки, які знаходяться на відстані 4 одиниць від 0.
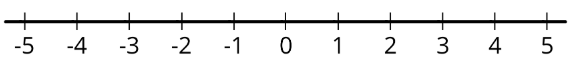
    clipboard_ee90aff7c0f6c92d9ad85ee9b99a1206f.png
    Малюнок\(\PageIndex{4}\)
    1. Якщо скласти цифру так, щоб вертикальна складка пройшла через 0, точки, які ви позначили, збігаються. Поясніть, чому так відбувається.
    2. На числовому рядку позначте точки, які є одиницями від 0. Яка відстань між цими точками?

    (З блоку 7.1.2)

    Вправа\(\PageIndex{8}\)

    Оцініть кожен вираз.

    • \(2^{3}\cdot 3\)
    • \(\frac{4^{2}}{2}\)
    • \(3^{1}\)
    • \(6^{2}\div 4\)
    • \(2^{3}-2\)
    • \(10^{2}+5^{2}\)

    (Від блоку 6.3.1)