36.4: Впорядкування раціональних чисел

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Урок

Давайте впорядкуємо раціональні числа.

Вправа $\PageIndex{1}$ : How Do They Compare?

Використовуйте символи >, < або = для порівняння кожної пари чисел. Будьте готові пояснити свої міркування.

$12\underline{\quad} 19$
$15\underline{\quad} 1.5$
$6.050\underline{\quad} 6.05$
$\frac{19}{24}\underline{\quad}\frac{19}{21}$
$212\underline{\quad} 190$
$9.02\underline{\quad} 9.2$
$0.4\underline{\quad}\frac{9}{40}$
$\frac{16}{17}\underline{\quad}\frac{11}{12}$

Вправа $\PageIndex{2}$ : Ordering Rational Number Cards

Ваш викладач дасть вам набір числових карток. Замовляйте їх від найменшого до найбільшого.

Ваш викладач дасть вам другий набір цифрових карт. Додайте їх до потрібних місць у впорядкованому наборі.

Вправа $\PageIndex{3}$ : Comparing Points on A Line

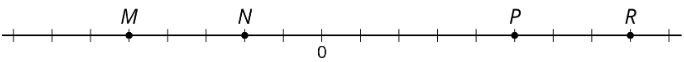
Використовуйте кожен з наступних термінів хоча б один раз для опису або порівняння значень балів $M, N, P, R$ .

більше, ніж
менше
протилежні (або протилежності)
негативне число

Скажіть, яким буде значення кожної точки, якщо:

$P$ є $2\frac{1}{2}$
$N$ є $-0.4$
$R$ є $200$
$M$ є $-15$

Ви готові до більшого?

Список дробів від 0 до 1 з знаменниками від 1 до 3 виглядає наступним чином:

$\frac{0}{1},\frac{1}{1},\frac{1}{2},\frac{1}{3},\frac{2}{3}$

Ми можемо привести їх у порядок так: $\frac{0}{1}<\frac{1}{3}<\frac{1}{2}<\frac{2}{3}<\frac{1}{1}$

Тепер давайте розширимо список, включивши дроби зі знаменниками $4$ . Ми не будемо включати $\frac{2}{4}$ , тому що вже $\frac{1}{2}$ є в списку.

$\frac{0}{1}<\frac{1}{4}<\frac{1}{3}<\frac{1}{2}<\frac{2}{3}<\frac{3}{4}<\frac{1}{1}$

Знову розгорніть список, щоб включити дроби, які мають знаменники $5$ .
Розгорніть список, який ви зробили, щоб включити дроби мають знаменники $6$ .
Коли ви додаєте новий дріб до списку, ви ставите його між двома «сусідами». Поверніться назад і подивіться на свою роботу. Чи бачите ви зв'язок між новою фракцією та двома її сусідами?

Резюме

Щоб упорядкувати раціональні числа від найменшого до найбільшого, перерахуємо їх у тому порядку, в якому вони з'являються на числовому рядку зліва направо. Наприклад, ми бачимо, що цифри

$-2.7, -1.3, 0.8$

перераховані від найменшого до найбільшого через порядок, який вони відображаються в рядку номера.

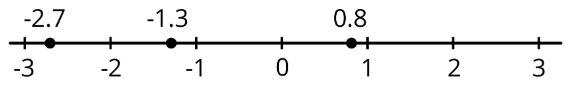
Записи глосарію

Визначення: Від'ємне число

Від'ємне число - це число, яке менше нуля. На горизонтальному числовому рядку від'ємні числа зазвичай відображаються ліворуч від 0.

Визначення: Протилежне

Два числа протилежні, якщо вони знаходяться на однаковій відстані від 0 і по різні боки числової лінії.

Наприклад, 4 - протилежність -4, а -4 - протилежність 4. Вони обидва мають однакову відстань від 0. Один негативний, а інший - позитивний.

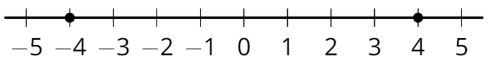
Визначення: Позитивне число

Позитивне число - це число, яке більше нуля. На горизонтальній числовій лінії позитивні числа зазвичай відображаються праворуч від 0.

Визначення: Раціональне число

Раціональне число - це дріб або протилежне дробу.

Наприклад, 8 і -8 є раціональними числами, оскільки їх можна записати як $\frac{8}{1}$ і $-\frac{8}{1}$ .

Крім того, 0,75 і -0,75 є раціональними числами, оскільки їх можна записати як $\frac{75}{100}$ і $-\frac{75}{100}$ .

Визначення: Знак

Знак будь-якого числа, відмінного від 0, є позитивним або негативним.

Наприклад, знак 6 позитивний. Знак -6 негативний. Нуль не має знака, тому що він не є позитивним або негативним.

Практика

Вправа $\PageIndex{4}$

Виділіть усі числа, які більше $-5$ .

$1.3$
$-6$
$-12$
$\frac{1}{7}$
$-1$
$-4$

Вправа $\PageIndex{5}$

Замовте ці числа від найменшого до найбільшого: $\frac{1}{2}, 0, 1, -1\frac{1}{2}, -\frac{1}{2}, -1$

Вправа $\PageIndex{6}$

Ось точки кипіння деяких елементів в градусах Цельсія:

Аргон: -185,8
Хлор: -34
Фтор: -188,1
Водень: -252,87
Криптон: -153.2

Перерахуйте елементи від найменшої до найбільшої точки кипіння.

Вправа $\PageIndex{7}$

Поясніть, чому нуль вважається своєю протилежністю.

(З блоку 7.1.2)

Вправа $\PageIndex{8}$

Поясніть, як зробити ці розрахунки подумки.

$99+54$
$244-99$
$99\cdot 6$
$99\cdot 15$

(Від одиниці 6.2.4)

Вправа $\PageIndex{9}$

Знайдіть коефіцієнти.

$\frac{1}{2}\div 2$
$2\div 2$
$\frac{1}{2}\div\frac{1}{2}$
$\frac{38}{79}\div\frac{38}{79}$

(Від блоку 4.3.2)

Вправа $\PageIndex{10}$

За кілька місяців вага малюка, виміряний в фунтах, подвоюється. Чи його вага, виміряна в кілограмах, також подвоюється? Поясніть.

(Від блоку 3.2.3)