36.2: Точки на числовій лінії

Last updated
Save as PDF

Page ID: 867

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Урок

Давайте побудуємо позитивні і негативні числа на числовому рядку.

Вправа\(\PageIndex{1}\): A Point on the Number Line

Яке з наступних чисел може бути\(B\)?

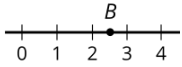
\(2.5\qquad\frac{2}{5}\qquad\frac{5}{2}\qquad\frac{25}{10}\qquad 2.49\)

Вправа\(\PageIndex{2}\): What's the Temperature?

Ось п'ять термометрів. Перші чотири термометри показують температуру за Цельсієм. Запишіть температури в заготовках.

Малюнок\(\PageIndex{2}\): П'ять вертикальних термометрів, а через е. термометр а затінюється до 1. Термометр b затінюють до 2. Термометр c затінюється до точки на півдорозі між 3 і 4. Термометр d затінюється на півдорозі між негативними 1 і 0. Термометр має галочки, позначені негативними 20, порожніми, порожніми, негативними 5, порожніми, порожніми, десятьма, порожніми, порожніми, 25.

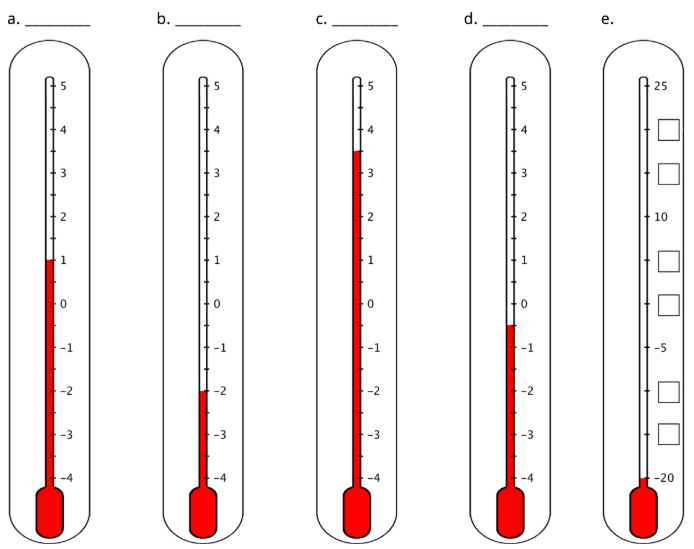
На останньому термометрі відсутні деякі цифри. Запишіть їх в ящики.

Олена каже, що показаний тут термометр читає\(-2.5^{\circ}\text{C}\) тому, що лінія рідини знаходиться вище\(-2^{\circ}\text{C}\). Джада каже, що це так\(-1.5^{\circ}\text{C}\). Чи згодні ви ні з одним з них? Поясніть свої міркування.

Одного ранку температура в Феніксі, штат Арізона, була\(8^{\circ}\text{C}\) і температура в Портленді, штат Мен, була\(12^{\circ}\text{C}\) прохолоднішою. Яка температура в Портленді?

Вправа\(\PageIndex{3}\): Folded Number Lines

Ваш викладач видасть вам аркуш кальки, на якому провести цифрову лінію.

Дотримуйтесь інструкцій, щоб створити свій власний номер рядка.
- За допомогою прямолінійки або лінійки намалюйте горизонтальну лінію. Відзначте середню точку лінії і позначте її 0.
- Праворуч від 0 намалюйте галочки, які знаходяться на відстані 1 сантиметр один від одного. Позначте галочками 1, 2, 3. 10. Це являє собою позитивну сторону вашого числового рядка.
- Складіть папір так, щоб вертикальна складка проходила через 0, а дві сторони цифрової лінії ідеально збігалися.
- Використовуйте згин, щоб допомогти вам простежити галочки, які ви вже намалювали на протилежній стороні цифрової лінії. Розгорніть і позначте галочками -1, -2, -3. -10. Це означає негативну сторону вашого числового рядка.
Використовуйте свій номер рядка, щоб відповісти на ці питання:
1. Яке число знаходиться на тій же відстані від нуля, як і число 4?
2. Яке число знаходиться на тій же відстані від нуля, як і число -7?
3. Два числа, які знаходяться на однаковій відстані від нуля на числовій лінії, називаються протилежностями. Знайдіть іншу пару протилежностей на числовій лінії.
4. Визначте, наскільки далеко знаходиться число 5 від 0. Потім виберіть додатне число і негативне число, яке кожне далі від нуля, ніж число 5.
5. Визначте, наскільки далеко знаходиться число -2 від 0. Потім виберіть додатне число і від'ємне число, яке кожне далі від нуля, ніж число -2.
  Пауза тут, щоб ваш викладач міг переглянути вашу роботу.
Ось числовий рядок з деякими точками, позначені літерами. Визначте розташування точок\(P, X,\) і\(Y\).

Якщо ви застрягли, простежте цифрову лінію і точки на аркуші кальки, складіть його так, щоб вертикальна складка пройшла через 0, і використовуйте згорнуту цифрову лінію, щоб допомогти вам знайти невідомі значення.

Ви готові до більшого?

Опівдні температури в Портленді, штаті Мен та Феніксі, штат Арізона, мали протилежні значення. Температура в Портленді була\(18^{\circ}\text{C}\) нижче, ніж у Феніксі. Яка температура була в кожному місті? Поясніть свої міркування.

Резюме

Ось числовий рядок, позначений додатними і від'ємними числами. Число 4 позитивне, тому його розташування становить 4 одиниці праворуч від 0 на числовому рядку. Число -1.1 є від'ємним, тому його розташування становить 1,1 одиниці ліворуч від 0 на числовому рядку.

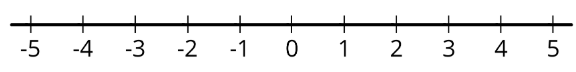
Ми говоримо, що протилежне 8.3 -8.3, і що \(\frac{-3}{2}\)протилежне є\(\frac{3}{2}\). Будь-які пари чисел, які однаково далекі від 0, називаються протилежностями.

Точки\(A\) і\(B\) є протилежностями, оскільки вони обидва знаходяться на відстані 2.5 одиниць від 0, хоча\(A\) знаходиться ліворуч від 0 і\(B\) знаходиться праворуч від 0.

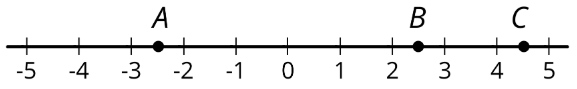
Позитивне число має негативне число для своєї протилежності. Від'ємне число має додатне число для своєї протилежності. Протилежність 0 сама по собі.

Ви працювали з позитивними числами протягом багатьох років. Усі позитивні числа, які ви побачили - цілі та нецілі числа - можуть розглядатися як дроби і розташовуватися на числовому рядку.

Щоб знайти неціле число на числовому рядку, ми можемо розділити відстань між двома цілими числами на дробові частини, а потім підрахувати кількість частин. Наприклад, 2.7 можна записати як\(2\frac{7}{10}\). Відрізок між 2 і 3 можна розділити на 10 рівних частин або 10 десятих. З 2 ми можемо відрахувати 7 десятих, щоб знайти 2.7 на цифровій лінії.

Всі дроби та їх протилежності - це те, що ми називаємо раціональними числами. Наприклад,\(4, -1.1, 8.3, -8.3, \frac{-3}{2},\) і всі\(\frac{3}{2}\) раціональні числа.

Записи глосарію

Визначення: Від'ємне число

Від'ємне число - це число, яке менше нуля. На горизонтальному числовому рядку від'ємні числа зазвичай відображаються ліворуч від 0.

Визначення: Протилежне

Два числа є протилежними, якщо вони знаходяться на однаковій відстані від 0 і по різні боки числової лінії.

Наприклад, 4 - протилежність -4, а -4 - протилежність 4. Вони обидва мають однакову відстань від 0. Один негативний, а інший - позитивний.

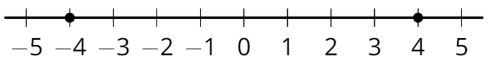
Визначення: Позитивне число

Позитивне число - це число, яке більше нуля. На горизонтальній числовій лінії позитивні числа зазвичай відображаються праворуч від 0.

Визначення: Раціональне число

Раціональне число - це дріб або протилежне дробу.

Наприклад, 8 і -8 є раціональними числами, оскільки їх можна записати як\(\frac{8}{1}\) і\(-\frac{8}{1}\).

Крім того, 0,75 і -0,75 є раціональними числами, оскільки їх можна записати як\(\frac{75}{100}\) і\(-\frac{75}{100}\).

Практика

Вправа\(\PageIndex{4}\)

Для кожного числа назвіть свою протилежність.

\(-5\)
\(28\)
\(-10.4\)

\(0.875\)
\(0\)
\(-8,003\)

Вправа\(\PageIndex{5}\)

Покладіть цифри\(-1.5, \frac{3}{2}, -\frac{3}{2},\) і\(-\frac{4}{3}\) на числовій лінії. Позначте кожну точку своїм числовим значенням.

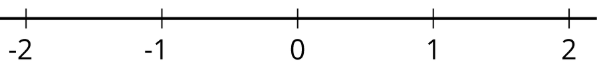
Вправа\(\PageIndex{6}\)

Покладіть ці точки на числовій лінії.

-1.5
протилежність -2
протилежність 0,5
-2

Вправа\(\PageIndex{7}\)

Представляють кожну з цих температур в градусах Фаренгейта з позитивним або негативним числом.
- \(5\)градусів вище нуля
- \(3\)градусів нижче нуля
- \(6\)градусів вище нуля
- \(2\frac{3}{4}\)градусів нижче нуля
Замовте температуру вище від найхолоднішої до найтеплішої.

(З блоку 7.1.1)

Вправа\(\PageIndex{8}\)

Вирішіть кожне рівняння.

\(8x=\frac{2}{3}\)
\(1\frac{1}{2}=2x\)
\(5x=\frac{2}{7}\)
\(\frac{1}{4}x=5\)
\(\frac{1}{5}=\frac{2}{3}x\)

(Від блоку 6.1.5)

Вправа\(\PageIndex{9}\)

Запишіть рішення до кожного рівняння у вигляді дробу та десяткового дробу.

\(2x=3\)
\(5y=3\)
\(0.3z=0.009\)

(Від блоку 6.1.5)

Вправа\(\PageIndex{10}\)

Є 15,24 сантиметра в 6 дюймах.

Скільки сантиметрів в 1 футі?
Скільки сантиметрів в 1 дворі?

(Від блоку 3.2.3)