3.6: Функції абсолютних значень
- Page ID
- 59354
Цілі навчання
- Графік функції абсолютного значення.
- Розв'яжіть рівняння абсолютного значення.
До 1920-х років так звані спіральні туманності вважалися хмарами пилу і газу в нашій власній галактиці, за кілька десятків тисяч світлових років. Тоді астроном Едвін Хаббл довів, що ці об'єкти є галактиками самі по собі, на відстанях мільйонів світлових років. Сьогодні астрономи можуть виявити галактики, які знаходяться на відстані мільярдів світлових років. Відстані у Всесвіті можна виміряти у всіх напрямках. Таким чином, корисно розглядати відстань як функцію абсолютного значення. У цьому розділі ми будемо досліджувати функції абсолютних значень.

Розуміння абсолютної цінності
Нагадаємо, що в базовому вигляді\(f(x)=|x|\) функція абсолютного значення є однією з функцій нашого інструментарію. Функція абсолютного значення зазвичай вважається забезпеченням відстані числа від нуля на числовому рядку. Алгебраїчно, для будь-якого вхідного значення, виходом є значення без урахування знака.
Функція абсолютного значення
Функція абсолютного значення може бути визначена як кускова функція
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Приклад\(\PageIndex{1}\): Determine a Number within a Prescribed Distance
Опишіть всі значення\(x\) в межах або включаючи відстань 4 від числа 5.
Рішення
Ми хочемо, щоб відстань між\(x\) і 5 була менше або дорівнює 4. Ми можемо намалювати числову лінію, наприклад, один в, щоб представити умова, яку потрібно задовольнити.

Відстань від\(x\) до 5 можна представити, використовуючи абсолютне значення як\(|x−5|\). Ми хочемо, щоб значення\(x\), які задовольняють умові\(| x−5 |\leq4\).
Аналіз
Зверніть увагу, що
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
Так\(|x−5|\leq4\) еквівалентно\(1{\leq}x\leq9\).
Однак математики взагалі віддають перевагу абсолютним значенням.
Вправа\(\PageIndex{1}\)
Опишіть всі значення на\(x\) відстані 3 від числа 2.
- Відповідь
-
\(|x−2|\leq3\)
Приклад\(\PageIndex{2}\): Resistance of a Resistor
Електричні деталі, такі як резистори і конденсатори, поставляються із заданими значеннями їх робочих параметрів: опір, ємність тощо Однак через неточність у виробництві фактичні значення цих параметрів дещо різняться від шматка до шматка, навіть коли вони повинні бути однаковими. Найкраще, що можуть зробити виробники, це спробувати гарантувати, що зміни залишатимуться в заданому діапазоні, часто ± 1%, ± 5% або ± 10%.
Припустимо, у нас резистор номінальний на 680 Ом, ± 5%. Використовуйте функцію абсолютного значення для вираження діапазону можливих значень фактичного опору.
Рішення
5% з 680 Ом становить 34 Ом. Абсолютне значення різниці між фактичним і номінальним опором не повинно перевищувати заявлену мінливість, так, при опорі\(R\) в Омах,
\[|R−680|\leq34 \nonumber\]
Вправа\(\PageIndex{2}\)
Студенти, які наберуть в межах 20 балів з 80, пройдуть тест. Запишіть це як відстань від 80, використовуючи абсолютні значення.
- Відповідь
-
Використовуючи змінну\(p\) для передачі,\(| p−80 |\leq20\)
Графік функції абсолютного значення
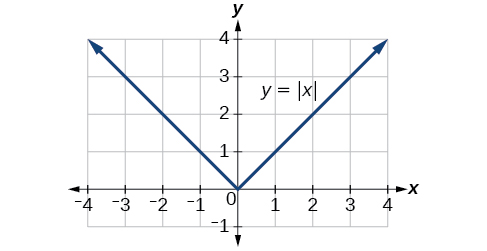
Найбільш значущою особливістю графіка абсолютних значень є кутова точка, в якій графік змінює напрямок. Ця точка показана у початку на малюнку\(\PageIndex{3}\).
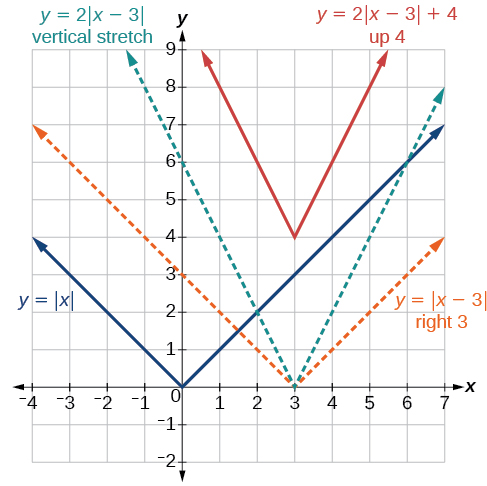
На малюнку\(\PageIndex{3}\) показаний графік\(y=2|x–3|+4\). Графік\(y=|x|\) був зміщений вправо на 3 одиниці, вертикально розтягнутий в 2 рази, і зміщений вгору на 4 одиниці. Це означає, що кутова точка розташована в\((3,4)\) для цієї трансформованої функції.
Приклад\(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
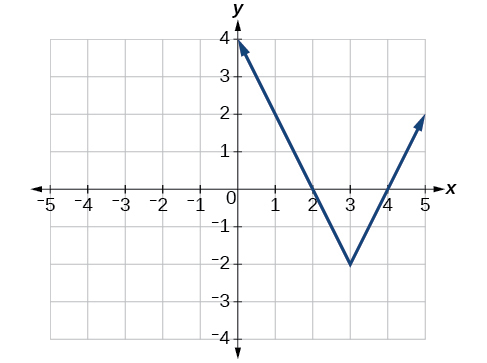
Напишіть рівняння для функції, зображеної на малюнку\(\PageIndex{5}\).
Рішення
Основна функція абсолютного значення змінює напрямок на початку, тому цей графік був зміщений вправо на 3 одиниці і вниз на 2 одиниці від основної функції інструментарію. Див\(\PageIndex{6}\). Малюнок.
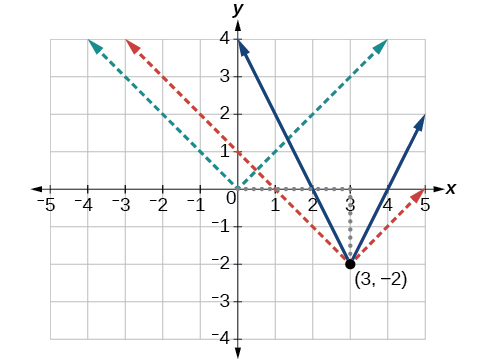
Ми також помічаємо, що графік виглядає вертикально розтягнутим, тому що ширина кінцевого графіка на горизонтальній лінії не дорівнює 2 рази відстані по вертикалі від кута до цієї лінії, як це було б для нерозтягнутої функції абсолютного значення. Замість цього ширина дорівнює 1 раз вертикальної відстані, як показано на малюнку\(\PageIndex{7}\).
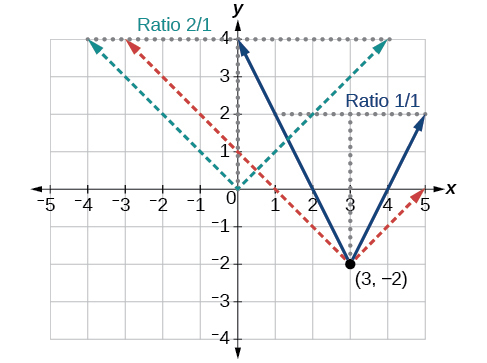
З цієї інформації ми можемо написати рівняння
\[\begin{align*} f(x)&=2|x-3|-2, \;\;\;\;\;\; \text{treating the stretch as a vertial stretch, or} \\ f(x)&=|2(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal compression.} \end{align*}\]
Аналіз
Зауважте, що ці рівняння алгебраїчно еквівалентні - розтягнення для функції абсолютного значення може бути записано взаємозамінно як вертикальне або горизонтальне розтягнення або стиснення.
Q & A
Якби ми не могли спостерігати розтягнення функції з графіків, чи могли б ми алгебраїчно визначити її?
- Відповідь
-
Так. Якщо ми не можемо визначити розтягнення на основі ширини графіка, ми можемо вирішити для коефіцієнта розтягування, поставивши відому пару значень для\(x\) і\(f(x)\).
\[f(x)=a|x−3|−2 \nonumber\]
Тепер підставляємо в точку\((1, 2)\)
\[\begin{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=2 \end{align*}\]
Вправа\(\PageIndex{3}\)
Запишіть рівняння для функції абсолютного значення, яка горизонтально зміщена вліво на 2 одиниці, вертикально перевертається і вертикально зміщена вгору на 3 одиниці.
- Відповідь
-
\(f(x)=−| x+2 |+3\)
Q & A
Чи завжди графіки функцій абсолютного значення перетинають вертикальну вісь? Горизонтальна вісь?
- Відповідь
-
Так, вони завжди перетинаються з вертикальною віссю. Графік функції абсолютного значення буде перетинати вертикальну вісь, коли вхід дорівнює нулю.
Ні, вони не завжди перетинаються з горизонтальною віссю. Графік може перетинатися або не перетинати горизонтальну вісь, залежно від того, як графік був зміщений і відображений. Функція абсолютного значення може перетинати горизонтальну вісь в нулі, одній або двох точках (рис.\(\PageIndex{8}\)).
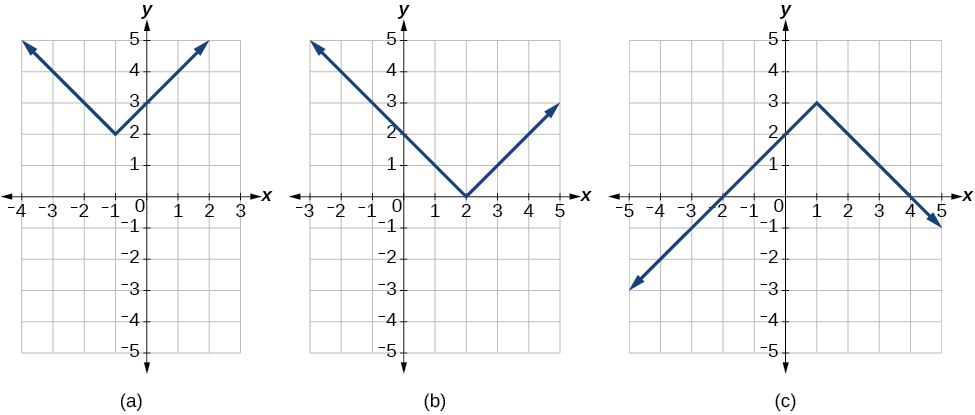
Малюнок\(\PageIndex{8}\): (а) Функція абсолютного значення не перетинає горизонтальну вісь. (b) Функція абсолютного значення перетинає горизонтальну вісь в одній точці. (c) Функція абсолютного значення перетинає горизонтальну вісь у двох точках.
Розв'язування рівняння абсолютного значення
Тепер, коли ми можемо графікувати функцію абсолютного значення, ми навчимося вирішувати рівняння абсолютного значення. Для вирішення такого рівняння\(8=|2x−6|\), як, ми помічаємо, що абсолютне значення буде дорівнює 8, якщо величина всередині абсолютного значення дорівнює 8 або -8. Це призводить до двох різних рівнянь, які ми можемо вирішити самостійно.
\[2x-6=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & x&=-1 \end{align*}\]
Знати, як вирішувати проблеми, пов'язані з функціями абсолютних значень, корисно. Наприклад, нам може знадобитися визначити числа або точки на лінії, які знаходяться на певній відстані від заданої контрольної точки.
Рівняння абсолютного значення - це рівняння, в якому невідома змінна з'являється в брусках абсолютних значень. Наприклад,
\[\begin{align*}|x|&=4, \nonumber \\[4pt] |2x−1| &=3, \\[4pt] |5x+2|−4 &=9. \end{align*}\]
Розв'язки рівнянь абсолютних значень
Для дійсних чисел\(A\) і\(B\), рівняння виду\(|A|=B\), з\(B\geq0\), матиме рішення коли\(A=B\) або\(A=−B\). Якщо\(B<0\), рівняння не\(|A|=B\) має розв'язку.
Як...
Задано формулу для функції абсолютного значення, знайдіть горизонтальні перехоплення її графіка.
- Виділяють абсолютне значення члена.
- \(|A|=B\)Використовувати для написання\(A=B\) або\(−A=B\), припускаючи\(B>0\).
- Вирішити для\(x\).
Приклад\(\PageIndex{4}\): Finding the Zeros of an Absolute Value Function
Для функції\(f(x)=|4x+1|−7\) знайдіть значення\(x\) такого, що\(f(x)=0\).
Рішення
\[\begin{align*} 0&=|4x+1|-7 & & &\text{Substitute 0 for f(x).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Break into two separate equations and solve.} \\ 6&=4x & -8&=4x & \\ x&=\frac{6}{4}=1.5 & x&=\frac{-8}{4}=-2 \end{align*}\]
Функція виводить 0 коли\(x=1.5\) або\(x=−2\) (рис.\(\PageIndex{9}\)).
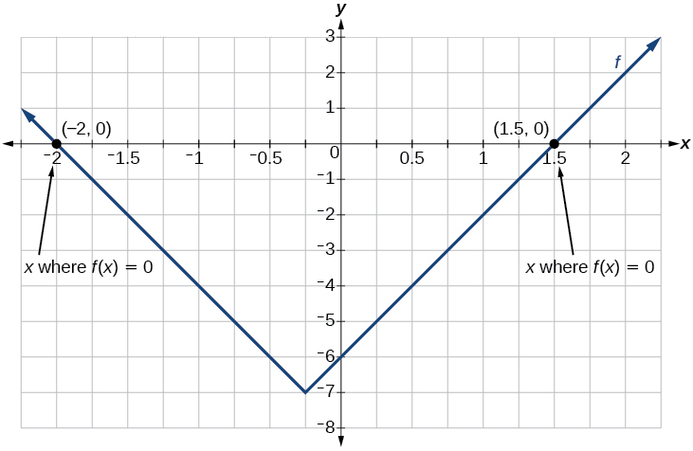
Вправа\(\PageIndex{4}\)
Для функції\(f(x)=|2x−1|−3\) знайдіть значення\(x\) такого, що\(f(x)=0\).
Рішення
\(x=−1\)або\(x=2\)
Q & A
Чи варто завжди очікувати двох відповідей при вирішенні\(|A|=B\)?
Відповідь
Ні. Ми можемо знайти один, два або навіть не відповідей. Наприклад, немає ніякого рішення\(2+|3x−5|=1\).
Як...
Задано рівняння абсолютного значення, розв'яжіть його.
- Виділяють абсолютне значення члена.
- \(|A|=B\)Використовувати для написання\(A=B\) або\(A=−B\).
- Вирішити для\(x\).
Приклад\(\PageIndex{5}\): Solving an Absolute Value Equation
Вирішити\(1=4|x−2|+2\).
Рішення
Виділення абсолютного значення на одній стороні рівняння дає наступне.
\[\begin{align*} 1&=4|x-2|+2 \\ -1&=4|x-2| \\ -\frac{1}{4}&=|x-2| \end{align*}\]
Абсолютне значення завжди повертає додатне значення, тому абсолютне значення не може дорівнювати від'ємному значенню. На цьому етапі ми помічаємо, що це рівняння не має розв'язків.
Q & A
У прикладі\(\PageIndex{5}\), якби\(f(x)=1\) і\(g(x)=4|x−2|+2\) були позначені на одному наборі осей, чи перетинаються графіки?
Відповідь
Ні. Графіки\(f\) і не\(g\) перетинаються, як показано на малюнку\(\PageIndex{10}\). Це підтверджує графічно, що рівняння не\(1=4|x−2|+2\) має рішення.
Знайти, де графік функції\(f(x)=−| x+2 |+3\) перетинає горизонтальну і вертикальну осі.
\(f(0)=1\), Таким чином, графік перетинає вертикальну вісь в\((0,1)\). \(f(x)=0\)коли\(x=−5\) і\(x=1\) так графік перетинає горизонтальну вісь в\((−5,0)\) і\((1,0)\).
Розв'язування абсолютної величини нерівності
Рівняння абсолютних значень не завжди можуть включати рівності. Натомість нам може знадобитися вирішити рівняння в діапазоні значень. Для розв'язання такого рівняння ми використали б абсолютну нерівність. Нерівність абсолютного значення - рівняння виду
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
або
\[ |A|{\geq}B, \nonumber\]
де вираз\(A\) (і, можливо, але не зазвичай\(B\)) залежить від змінної\(x\). Вирішення нерівності означає знаходження сукупності всього\(x\), що задовольняє нерівності. Зазвичай цей набір буде інтервалом або об'єднанням двох інтервалів.
Існує два основних підходи до розв'язання абсолютних величин нерівностей: графічний та алгебраїчний. Перевага графічного підходу полягає в тому, що ми можемо прочитати рішення шляхом інтерпретації графіків двох функцій. Перевага алгебраїчного підходу полягає в тому, що він дає рішення, які можуть бути важко прочитати з графіка.
Наприклад, ми знаємо, що всі числа в межах 200 одиниць 0 можуть бути виражені як
\[|x|<200 \nonumber\]
або
\[ −200<x<200 \nonumber\]
Припустимо, ми хочемо знати всі можливі прибутки від інвестицій, якщо ми могли б заробити певну суму грошей в межах $200 або $600. Ми можемо вирішити алгебраїчно для набору значень,\(x\) таких, що відстань між\(x\) і 600 менше 200. Уявляємо відстань між\(x\) і 600 як\(|x−600|\).
\[|x−600|<200\]
або
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
Це означає, що наші прибутки становитимуть від 400 до 800 доларів.
Іноді проблема нерівності абсолютних значень буде представлена нам через зсунуту та/або розтягнуту або стиснуту функцію абсолютного значення, де ми повинні визначити, для яких значень вхідних результатів функції буде від'ємним або позитивним.
Як...
З огляду на абсолютну величину нерівності виду\(|x−A|{\leq}B\) для дійсних чисел\(a\) і\(b\) де\(b\) є додатним, розв'яжіть абсолютну величину нерівності алгебраїчно.
- Знайти граничні точки шляхом розв'язання\(|x−A|=B\).
- Тестові інтервали створюються граничними точками, щоб визначити, де\(|x−A|{\leq}B\).
- Запишіть інтервал або об'єднання інтервалів, що задовольняють нерівності в інтервалі, нерівності або множинних позначеннях.
Приклад\(\PageIndex{6}\): Solving an Absolute Value Inequality
Вирішити\(|x −5|{\leq}4\).
Рішення
При обох підходах нам потрібно буде спочатку знати, де відповідна рівність відповідає дійсності. У цьому випадку ми спочатку знайдемо де\(|x−5|=4\). Ми робимо це тому, що абсолютне значення є функцією без перерв, так що єдиний спосіб значення функції можуть перемикатися від бути менше 4 бути більше, ніж 4 є шляхом проходження через де значення рівні 4. Вирішити\(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
Визначивши, що абсолютне значення дорівнює 4 в\(x=1\) і\(x=9\), ми знаємо, що графік може змінюватися тільки від менше 4 до більше 4 при цих значеннях. Це ділить числовий рядок вгору на три інтервали:
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
Щоб визначити, коли функція менше 4, ми могли б вибрати значення в кожному інтервалі і подивитися, чи результат менше або більше 4, як показано в табл\(\PageIndex{1}\).
| Інтервальний тест\(x\) | \(f(x)\) | \(<4\)або\(>4\) | |
|---|---|---|---|
| \ (x\)» style="вертикальне вирівнювання: середина; ">\(x<1\) | \ (f (x)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (<4\) або\(>4\) "style="вертикальне вирівнювання: середина;" >\(|0-5|=5\) | Більше, ніж |
| \ (x\)» style="вертикальне вирівнювання: середина; ">\(1<x<9\) | \ (f (x)\)» style="вертикальне вирівнювання: середина; "> 6 | \ (<4\) або\(>4\) "style="вертикальне вирівнювання: середина;" >\(|6-5|=1\) | Менше |
| \ (x\)» style="вертикальне вирівнювання: середина; ">\(x>9\) | \ (f (x)\)» style="вертикальне вирівнювання: середина; "> 11 | \ (<4\) або\(>4\) "style="вертикальне вирівнювання: середина;" >\(|11-5|=6\) | Більше, ніж |
Оскільки\(1{\leq}x{\leq}9\) це єдиний інтервал, в якому вихід при тестовому значенні менше 4, можна зробити висновок, що рішення до\(|x−5|{\leq}4\) є\(1{\leq}x{\leq}9\), або\([1,9]\).
Щоб використовувати графік, ми можемо намалювати функцію\(f(x)=|x−5|\). Щоб допомогти нам побачити, де виходи 4, лінію також\(g(x)=4\) можна намалювати, як на малюнку\(\PageIndex{11}\).
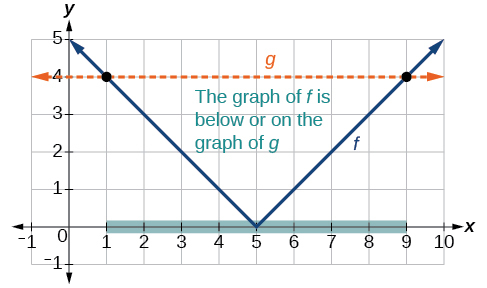
Ми можемо побачити наступне:
- Вихідні значення абсолютного значення дорівнюють 4 в\(x=1\) і\(x=9\).
- Графік\(f\) знаходиться нижче графіка\(g\) на\(1<x<9\). Це означає, що вихідні значення\(f(x)\) менше вихідних значень\(g(x)\).
- Абсолютне значення менше або дорівнює 4 між цими двома точками, коли\(1{\leq}x\leq9\). У інтервальних позначеннях це буде інтервал\([1,9]\).
Аналіз
Для нерівностей абсолютних значень,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
\(>\)Символ\(<\) або може бути замінений на\(\leq\) або\(\geq\).
Отже, для цього прикладу ми могли б використовувати цей альтернативний підхід.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]
Вправа\(\PageIndex{5}\)
Вирішити\(|x+2| \leq 6\).
- Відповідь
-
\(-8 \leq x \leq 4\)
Як...
Задано функцію абсолютного значення, розв'яжіть для множини входів, де вихід є додатним (або від'ємним).
- Встановіть функцію рівну нулю, і вирішіть для граничних точок множини розв'язку.
- Використовуйте контрольні точки або графік, щоб визначити, де результат функції є позитивним або негативним.
Приклад\(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
Задано функцію\(f(x)=−\frac{1}{2}|4x−5|+3\), визначте\(x\) -значення, для яких значення функції є від'ємними.
Рішення
Ми намагаємося визначити\(f(x)<0\), де, що коли\(−\frac{1}{2}|4x−5|+3<0\). Починаємо з виділення абсолютної величини.
\[ \begin{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−5|&>6\end{align*}\]
Далі вирішуємо за рівність\(|4x−5|=6\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=6 \end{align*}\]
або
\[\begin{align*} 4x&=-1 \\ x&=\frac{11}{4} & x&=-\frac{1}{4} \end{align*}\]
Тепер ми можемо вивчити графік,\(f\) щоб спостерігати, де вихід негативний. Будемо спостерігати, де гілки знаходяться нижче\(x\) -осі. Зверніть увагу, що навіть не важливо, як саме виглядає графік, якщо ми знаємо, що він перетинає горизонтальну вісь\(x=−\frac{1}{4}\)\(x=\frac{11}{4}\) і що графік був відображений вертикально. Див\(\PageIndex{12}\). Малюнок.
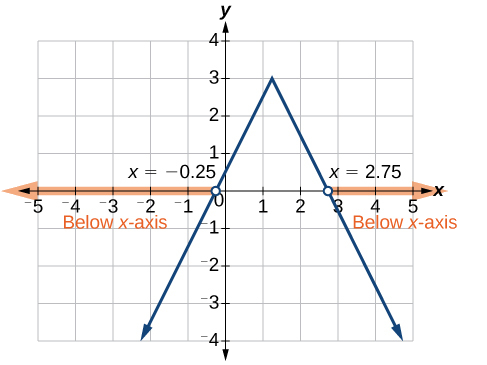
Ми спостерігаємо, що графік функції знаходиться нижче\(x\) -осі зліва\(x=−\frac{1}{4}\) і праворуч від\(x=\frac{11}{4}\). Це означає, що значення функції від'ємні зліва від першого горизонтального перехоплення в\(x=−\frac{1}{4}\), і негативні праворуч від другого перехоплення в\(x=\frac{11}{4} \). Це дає нам рішення нерівності.
\[x<−\frac{1}{4} \text{ or } x>1\frac{1}{4} \nonumber\]
У інтервальних позначеннях це було б\(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Вправа\(\PageIndex{6}\)
Вирішити\(−2|k−4|\leq−6\).
- Відповідь
-
\(k\leq1\)або\(k\geq7\); в інтервальному позначенні це було б\(\left(−\infty,1\right]\cup\left[7,\infty\right)\)
Ключові концепції
- Функція абсолютного значення зазвичай використовується для вимірювання відстаней між точками.
- Прикладні задачі, такі як діапазони можливих значень, також можуть бути вирішені за допомогою функції абсолютних значень.
- Графік функції абсолютного значення нагадує букву V. Він має кутову точку, в якій графік змінює напрямок.
- У рівнянні абсолютного значення невідома змінна є входом функції абсолютного значення.
- Якщо абсолютне значення виразу встановлено рівним додатному числу, очікуйте два розв'язки для невідомої змінної.
- Рівняння абсолютного значення може мати одне рішення, два розв'язки або не розв'язки.
- Нерівність абсолютних значень подібна до рівняння абсолютного значення, але набуває вигляду | A |B<B, | A |≤B, | A |>, або | A |≥B.Це може бути вирішено шляхом визначення меж множини розв'язку, а потім тестування, які сегменти знаходяться в множині.
- Нерівності абсолютних значень також можуть бути вирішені графічно.
Глосарій
абсолютне значення
рівняння рівняння виду\(|A|=B\), з\(B\geq0\); він матиме рішення, коли\(A=B\) або\(A=−B\)
абсолютна величина нерівності
відносини у вигляді\(|A|<B\),,\(|A|{\leq}B\),\(|A|>B\), або\(|A|{\geq}B\)
