4.3: Рівняння

Рівняння

Рівняння

Рівняння - це твердження, що два алгебраїчні вирази рівні

Рівняння складається з трьох частин.

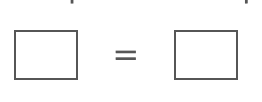
Кожна з коробок являє собою алгебраїчний вираз. Рівняння складається з двох виразів, розділених знаком рівності. Знак рівності робить твердження, що два вирази еквівалентні, тобто вони представляють одне і те ж значення. Наприклад:

Приклад$\PageIndex{1}$

$f = 32a$

Рівняння виражає зв'язок між змінними$f$ і$a$. У ньому зазначено, що значення$f$ завжди в$32$ рази більше, ніж$a$.

Приклад$\PageIndex{2}$

$y = 6x + 8$

Рівняння виражає зв'язок між змінними$x$ і$y$. У ньому зазначено, що значення$y$ завжди$8$ більше, ніж в$6$ рази перевищує значення$x$.

Чисельна оцінка

Чисельна оцінка

Чисельна оцінка - це процес визначення значення шляхом підстановки цифр на букви.

Формули

У різних сферах (бізнес, статистика, фізика, хімія, астрономія, соціологія, психологія і т.д.) конкретні рівняння зустрічаються досить часто. Такі рівняння називаються формулами. Чисельна оцінка часто використовується з формулами.

Набір зразків A

Приклад$\PageIndex{3}$

$f = 32a$. Визначаємо значення$f$ є$a = 2$

$f = 32(2)$. Замінити$a$ на$2$.

$= 64$

Приклад$\PageIndex{4}$

$p = \dfrac{10,000}{v}$.

Це рівняння хімії виражає$p$ залежність між тиском газу та$v$ об'ємом газу.

Визначте значення$p$ if$v = 500$.

$p = \dfrac{10,000}{500}$Замінити$v$ на$500$

Приклад$\PageIndex{5}$

$z = \dfrac{x-u}{s}$.

Це статистичне рівняння виражає зв'язок між змінними$z, x, u$, і$s$. Визначте значення$z$ є$x = 41$$u = 45$, і$s = 1.3$. Округлення до двох знаків після коми.

$\begin{aligned} z &=\dfrac{41-45}{1.3} \\ &=\dfrac{-4}{1.3} \\ &=-3.08 \end{aligned}$

Приклад$\PageIndex{6}$

$p = 5w^3 + w^2 - w - 1$.

Це рівняння виражає взаємозв'язок між$p$ і$w$. Визначте значення$p$ if$w = 5$.

$\begin{aligned} p &=5(5)^{3}+(5)^{2}-(5)-1 \\ &=5(125)+25-(5)-1 \\ &=625+25-5-1 \\ &=644 \end{aligned}$

Практика Set A

Завдання практики$\PageIndex{1}$

$f = 32a$. Визначте значення$f$ if$a = 6$.

Відповідь

$192$

Завдання практики$\PageIndex{2}$

$p = \dfrac{10,000}{v}$. Визначте значення$p$ є$v = 250$.

Відповідь

$40$

Завдання практики$\PageIndex{3}$

$F = \dfrac{9}{5}C + 32$. Визначаємо значення$F$ if$C = 10$

Відповідь

$50$

Завдання практики$\PageIndex{4}$

$y = -9x - 14$. Визначте значення$y$ if$x = -3$.

Відповідь

$13$

Завдання практики$\PageIndex{5}$

$m = 5p^3 - 2p + 7$. Визначте значення$m$ if$p = -2$.

Відповідь

$-29$

Вправи

Для наступних задач дотримуйтесь рівнянь і констатуйте виражається взаємозв'язок.

Вправа$\PageIndex{1}$

$x = 6y$

Відповідь

Значення$x$ дорівнює шестикратному значенню$y$.

Вправа$\PageIndex{2}$

$y = x + 4$

Вправа$\PageIndex{3}$

$e = g - 9$

Відповідь

$e$дорівнює$9$ меншому, ніж значення$g$.

Вправа$\PageIndex{4}$

$y = x - 7$

Вправа$\PageIndex{5}$

$3t = 6s$

Відповідь

Значення в три рази$t$ дорівнює шести разів$s$.

Вправа$\PageIndex{6}$

$u = v^5$

Вправа$\PageIndex{7}$

$r = \dfrac{2}{9}s$

Відповідь

Значення$r$ дорівнює двом дев'ятим кратам значення$s$.

Вправа$\PageIndex{8}$

$b = \dfrac{3}{4}a$

Вправа$\PageIndex{9}$

$f = 0.97k + 55$

Відповідь

Значення$f$ дорівнює$55$ більш ніж$\dfrac{97}{100}$ кратного значення$k$.

Вправа$\PageIndex{10}$

$w = 4z^3 - 21$

Вправа$\PageIndex{11}$

$q^2 = 9x^8 + 2y$

Відповідь

Значення$q^2$ дорівнює дев'яти кратним значенням$x^8$ плюс два рази більше значення$y$.

Вправа$\PageIndex{12}$

$I = m^2qb^5 + 3.115p$

Використовуйте числове оцінювання на рівняннях для наступних задач.

Вправа$\PageIndex{13}$

Геометрія (окружність кола)
$C = 2\pi r$. Знайти$\pi$,$C$ якщо це наближено$3.14$ і$r = 5$

Відповідь

$31.4$

Вправа$\PageIndex{14}$

Геометрія (площа прямокутника)

$A = lw$. Знайти$A$, якщо$l = 15$ і$w = 9$.

Вправа$\PageIndex{15}$

Електрика (струм в ланцюзі)

$I = \dfrac{E}{R}$. Знайти$I$, якщо$E = 21$ і$R = 7$.

Відповідь

$3$

Вправа$\PageIndex{16}$

Електрика (струм в ланцюзі)

$I = \dfrac{E}{R}$. Знайти$I$, якщо$E = 106$ і$R = 8$.

Вправа$\PageIndex{17}$

Бізнес (простий інтерес)

$I = prt$. Знайти$p = 3000$,$I$ якщо$r = 0.12$, і$t = 1$.

Відповідь

$360$

Вправа$\PageIndex{18}$

Бізнес (простий інтерес)

$I = prt$. Знайти$p = 250$,$I$ якщо$r = 0.07$, і$t = 6$.

Вправа$\PageIndex{19}$

Геометрія (площа паралелограма)

$A = bh$. Знайти$A$, якщо$b = 16$ і$h = 6$.

Відповідь

$96$

Вправа$\PageIndex{20}$

Геометрія (площа трикутника)

$A = \dfrac{1}{2}bh$. Знайти$A$, якщо$b = 25$ і$h = 10$.

Вправа$\PageIndex{21}$

Геометрія (периметр прямокутника)

$P = 2l + 2w$. Знайти$P$, якщо$l = 3$ і$w = 1$.

Відповідь

$8$

Вправа$\PageIndex{22}$

Геометрія (периметр прямокутника)

$P = 2l + 2w$. Знайти$P$, якщо$l = 74$ і$w = 16$.

Вправа$\PageIndex{23}$

Геометрія (периметр прямокутника)

$P = 2l + 2w$. Знайти$P$, якщо$l = 8\dfrac{1}{4}$ і$w = 12\dfrac{8}{9}$.

Відповідь

$42\dfrac{5}{18}$

Вправа$\PageIndex{24}$

Фізика (сила)

$F = 32m$. Знайти,$F$ якщо$m = 6$.

Вправа$\PageIndex{25}$

Фізика (сила)

$F = 32m$. Знайти,$F$ якщо$m = 14$.

Відповідь

$448$

Вправа$\PageIndex{26}$

Фізика (сила)

$F = 32m$. Знайти,$F$ якщо$m = 14$.

Відповідь

$448$

Вправа$\PageIndex{27}$

Фізика (сила)

$F = 32m$. Знайти,$F$ якщо$m = 6.42$.

Відповідь

$205.44$

Вправа$\PageIndex{28}$

Фізика (імпульс)

$p = mv$. Знайти,$p$ якщо$m = 18$ і$v = 5$

Вправа$\PageIndex{29}$

Фізика (імпульс)

$p = mv$. Знайти,$p$ якщо$m = 44$ і$v = 9$

Відповідь

$396$.

Вправа$\PageIndex{30}$

Фізика (імпульс)

$p = mv$. Знайти,$p$ якщо$m = 9.18$ і$v = 16.5$

Вправа$\PageIndex{31}$

Фізика (енергетика)

$E = \dfrac{1}{2}mv^2$. Знайти$E$, якщо$m = 12$ і$v = 5$.

Відповідь

$150$

Вправа$\PageIndex{32}$

Фізика (енергетика)

$E = \dfrac{1}{2}mv^2$. Знайти$E$, якщо$m = 8$ і$v = 15$.

Вправа$\PageIndex{33}$

Фізика (енергетика)

$E = \dfrac{1}{2}mv^2$. Знайти$E$, якщо$m = 24.02$ і$v = 7$.

Відповідь

$588.49$

Вправа$\PageIndex{34}$

Астрономія (закон Кеплера про рух планет)

$P^2 = ka^3$. Знайти$P^2$, якщо$k = 1$ і$a = 4$.

Вправа$\PageIndex{35}$

Астрономія (закон Кеплера про рух планет)

$P^2 = ka^3$. Знайти$P^2$, якщо$k = 8$ і$a = 31$.

Відповідь

238 328

Вправа$\PageIndex{36}$

Астрономія (закон Кеплера про рух планет)

$P^2 = ka^3$. Знайти$P^2$, якщо$k = 4$ і$a = 5.1$.

Вправа$\PageIndex{37}$

Астрономія (закон Кеплера про рух планет)

$P^2 = ka^3$. Знайти$P^2$, якщо$k = 53.7$ і$a = 0.7$.

Відповідь

$18.4191$

Вправа$\PageIndex{38}$

Бізнес (прибуток, дохід і вартість)

$P = R - C$. Знайти$P$, якщо$R = 3100$ і$C = 2500$.

Вправа$\PageIndex{39}$

Бізнес (прибуток, дохід і вартість)

$P = R - C$. Знайти$P$, якщо$R = 4240$ і$C = 3590$.

Відповідь

$650$

Вправа$\PageIndex{40}$

Геометрія (площа кола)

$A = \pi r^2$. Знайти$\pi$,$A$ якщо приблизно$3.14$ і$r = 3$.

Вправа$\PageIndex{41}$

Геометрія (площа кола)

$A = \pi r^2$. Знайти$\pi$,$A$ якщо приблизно$3.14$ і$r = 11$.

Відповідь

$379.94$

Вправа$\PageIndex{42}$

$t = 21x + 6$. Знайти$t$ якщо$x = 3$

Вправа$\PageIndex{43}$

$t = 21x + 6$. Знайти$t$ якщо$x = 97$

Відповідь

$2,043$

Вправа$\PageIndex{44}$

$E = mc^2$. Знайти$E$, якщо$m = 2$ і$c = 186,000$.

Вправа$\PageIndex{45}$

$E = mc^2$. Знайти$E$, якщо$m = 5$ і$c = 186,000$.

Відповідь

$1.7298 \times 10^{11}$.

Вправа$\PageIndex{46}$

Об'єкт рухається по горизонтальній лінії. Відстань, яку вона проходить, представлена$d$ і вимірюється в метрах. Рівняння,$t$ що стосується часу подорожі та відстані подорожі, є
$d=t2−4t+20$
Визначте відстань$d$, пройдену об'єктом, якщо він перебував у русі протягом$6$ секунд.

Вправа$\PageIndex{47}$

У медицині існує кілька практичних правил, які використовуються медиками для визначення дози дитини$D_c$, конкретного препарату. Одне з таких правил, правило Янга, пов'язує дозу препарату дитини до дорослої дози цього препарату,$D_a$. Правило Янга

$D_c = \dfrac{t}{t+12} \cdot D_a$

$t$де вік дитини в роках. Що потрібно давати дитині 8 років, якщо відповідна дозування дорослої людини становить 15 одиниць?

Відповідь

6 одиниць

Вправа$\PageIndex{48}$

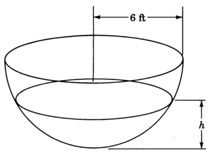
Напівсферичний резервуар для води$6$ радіусних ніг має воду, що капає в нього. Рівняння, що стосується обсягу$V$, води в резервуарі в будь-який час є$V=6\pi h^2−\pi 3h^3$, де$h$ являє собою глибину води. Використовуючи$3.14$ для наближення нераціональне число$\pi$, визначте обсяг води в баку при глибині води$3$ футів.

Вправа$\PageIndex{49}$

Рівняння було$W=3.51L−192$ встановлено Міжнародною китобійною комісією, щоб пов'язати вагу$W$ (у довгих тонн) зрілого синього кита з його довжиною$L$ (у футах). Рівняння використовується лише тоді, коли$L \ge 70$. Коли
$0<L<70$
сині кити вважаються незрілими. При народженні синій кит має довжину приблизно$24$ ноги. Визначте вагу синього кита, який вимірює$83$ ноги в довжину.

Відповідь

$99.33$тонн

Вправа$\PageIndex{50}$

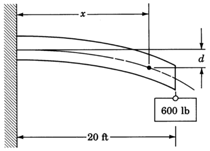
Існує залежність між довжиною консольної балки та величиною, яку вона відхиляється, коли вага прикріплюється до її кінця. Якщо$20$ ноги консольної балки довжиною мають вагу$600$ фунта, прикріплений до його кінця, рівняння, що стосується довжини балки та величини відхилення, є

$d = \dfrac{60x^2-x^3}{16,000}$

де$d$ - величина прогину, виміряна в дюймах і$x$ - довжина від опорної частини балки до якоїсь точки на балці, в якій вимірюється величина прогину. Знайдіть величину відхилення$17$ ніг балки від опорного кінця.

Вправа$\PageIndex{51}$

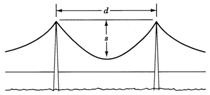
Існує залежність між довжиною кабелю підвісного моста, який закріплений між двома вертикальними опорами, і величиною провисання кабелю. Якщо уявити довжину кабелю по$c$, горизонтальне відстань між вертикальними опорами по$d$, а величина провисання по$s$, рівняння дорівнює$c=d + \dfrac{8s^2}{3d} - \dfrac{32s^4}{5d^3}$. Якщо горизонтальна відстань між двома вертикальними опорами становить$190$ ноги, а кількість провисання в кабелі, який підвішений між двома опорами, становить$20$ ноги, яка довжина кабелю?

Відповідь

$195.46474$

Вправи для огляду

Вправа$\PageIndex{52}$

Спростити$(4x^3y^8)(3x^2y)$

Вправа$\PageIndex{53}$

Спростити$-|-8|$

Відповідь

$-8$

Вправа$\PageIndex{54}$

Знайдіть значення$4^{-2} \cdot 8^2 - 3^2$.

Вправа$\PageIndex{55}$

Для виразу напишіть кількість членів$5(a + b) + 2x^2$, які з'являються, а потім напишіть самі терміни.

Відповідь

$2; 5(a + b), 2x^2$

Вправа$\PageIndex{56}$

Скільки їх$xy^3$ там$5x^2y^5$?