2.5: Показники

Last updated
Save as PDF

Page ID: 58603

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Огляд

Експоненціальне позначення
Читання експоненціальних позначень
Порядок операцій

Експоненціальне позначення

У розділі 2.4 нам нагадали, що множення - це опис для повторного додавання. Природним питанням є «Чи є опис для повторного множення?» Відповідь - так. Позначення, що описує повторне множення, - це експоненціальні позначення.

Фактори

При множенні числа, що множаться разом, називаються множниками. При повторному множенні всі фактори однакові. При неповторному множенні жоден з факторів не збігається. Наприклад,

Приклад$\PageIndex{1}$

$18 \cdot 18 \cdot 18 \cdot 18$Повторне множення 18. Всі чотири фактори, 18 однакові.

$x \cdot x \cdot x \cdot x \cdot x$Повторне множення$x$. Всі п'ять факторів однакові.$x$

$3 \cdot 7 \cdot a$Неповторне множення. Жоден з факторів не є однаковим.

Експоненціальне позначення використовується для показу повторного множення одного і того ж коефіцієнта. Позначення складається з використання верхнього індексу на факторі, який повторюється. Верхній індекс називається експонентою.

Експоненціальне позначення

Експоненціальне позначення Якщо$x$ будь-яке дійсне число і$n$ є натуральним числом, то

$x^{n}=\underbrace{x \cdot x \cdot x \cdot \ldots \cdot x}_{n \text { factors of } x}$

показник записує кількість однакових факторів при множенні.

Зауважте, що визначення для експоненціального позначення має значення лише для натуральних числових показників. Ми продовжимо це позначення, щоб пізніше включити інші числа як експоненти.

Набір зразків A

Приклад$\PageIndex{2}$

$7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 \cdot 7 = 7^6$

Повторний коефіцієнт дорівнює 7. Показник 6 фіксує той факт, що 7 з'являється 6 разів у множенні.

Приклад$\PageIndex{3}$

$x \cdot x \cdot x \cdot x = x^4$

Повторний фактор є$x$. Показник 4 фіксує той факт, що$x$ з'являється 4 рази в множенні.

Приклад$\PageIndex{4}$

$(2y)(2y)(2y) = (2y)^3$

Повторний фактор є$2y$. Показник 3 фіксує той факт, що коефіцієнт$2y$ з'являється 3 рази при множенні.

Приклад$\PageIndex{5}$

$2yyy = 2y^3$

Повторний фактор є$y$. Показник 3 фіксує той факт, що коефіцієнт$y$ з'являється 3 рази при множенні.

Приклад$\PageIndex{6}$

$(a + b)(a + b)(a - b)(a - b)(a - b) = (a + b)^2(a - b)^3$

Повторними факторами є$(a + b)$ і$(a - b)$,$(a + b)$ з'являються 2 рази і$(a - b)$ з'являються 3 рази.

Практика Set A

Запишіть кожне з наступних, використовуючи експоненти.

Завдання практики$\PageIndex{1}$

$a \cdot a \cdot a \cdot a$

Відповідь: $a^4$

Завдання практики$\PageIndex{2}$

$(3b)(3b)(5c)(5c)(5c)(5c)$

Відповідь: $(3b)^2(5c)^4$

Завдання практики$\PageIndex{3}$

$2 \cdot 2 \cdot 7 \cdot 7 \cdot 7 \cdot (a - 4)(a - 4)$

Відповідь: $2^2 \cdot 7^3(a - 4)^2$

Завдання практики$\PageIndex{4}$

$8xxxyzzzzz$

Відповідь: $8x^3yz^5$

Набір зразків B

Приклад$\PageIndex{7}$

$8x^3$значить$8 \cdot xxx$ і ні$8x8x8x$. Показник$3$ застосовується лише до фактора,$x$ оскільки це лише до того фактора$x$, який$3$ пов'язаний.

Приклад$\PageIndex{8}$

$(8x)^3$означає,$(8x)(8x)(8x)$ оскільки дужки вказують на те, що$3$ показник безпосередньо пов'язаний з коефіцієнтом$8x$. Пам'ятайте, що символи групування () вказують на те, що величини всередині повинні розглядатися як одне єдине число.

Приклад$\PageIndex{9}$

$34(a+1)^2$означає$34 \cdot (a+1)(a+1)$, що показник$2$ застосовується тільки до фактора$(a+1)$.

Практика Set B

Запишіть кожне з наведених нижче показників без показників.

Завдання практики$\PageIndex{5}$

$4a^3$

Відповідь: $4aaa$

Завдання практики$\PageIndex{6}$

$(4a)^3$

Відповідь: $(4a)(4a)(4a)$

Набір зразків C

Приклад$\PageIndex{10}$

Виберіть число для показу,$(2 x)^{2}$ яке не завжди дорівнює$2 x^{2}$.
Припустимо, ми$x$ вибираємо бути 5. Розглянемо обидва$(2 x)^{2}$ і$2 x^{2}$.
\ (
\ почати {масив} {ll}
(2 x) ^ {2} & 2 x ^ {2}\\
(2\ cdot 5) ^ {2} & 2\ cdot 5^ {2}\\
(10) ^ {2} & 2\ cdot 25\\
100 &\ neq 50
\ end {масив}
\)
Зверніть увагу, що $(2 x)^{2}=2 x^{2}$тільки коли$x=0$.

Практика Set C

Завдання практики$\PageIndex{7}$

Виберіть число для показу,$(5x)^2$ яке не завжди дорівнює$5x^2$

Відповідь: Виберіть$x=3$. Потім$(5 \cdot 3)^2 = (15)^2 = 225$, але$5 \cdot 3^2 = 5 \cdot 9 = 45$. $225 \not = 45$

Читання експоненціальних позначень

$ln(x^n)$

Підстава
$x$ - це основа.

Показник експоненти
$n$ є показником.

Потужність. Число,$x^n$ представлене, називається степенем.

$x$до
Сили Термін$x^n$ читається як «$x$до$n$ владі», або простіше кажучи як «$x$до$n$ го».$n$

$x$Квадрат і$x$ куб

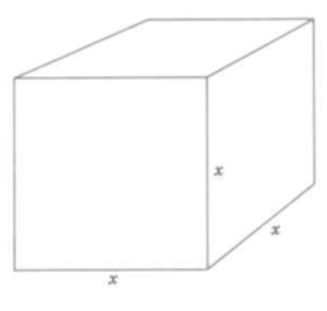
Символ часто$x^2$ читається як «$x$квадрат», і часто$x^3$ читається як «$x$куб». Природним питанням є «Чому геометричні терміни з'являються в експонентному вираженні?» Відповідь за$x^3$ така:$x^3$ значить$x \cdot x \cdot x$. У геометрії обсяг прямокутної коробки знаходять шляхом множення довжини на ширину на глибину. Куб має однакову довжину з кожного боку. Якщо уявити цю довжину буквою,$x$ то обсяг куба дорівнює$x \cdot x \cdot x$, який, звичайно, описується$x^3$. (Чи можете ви придумати$x^2$, чому читається як$x$ квадрат?)

Куб з

довжина =$x$
ширина =$x$
глибина =$x$
обсяг =$xxx$ =$x^3$

$clipboard_e5a24204a712094a23f76f8e8f4952e4b.png$

Порядок операцій

У розділі 4.2 ми познайомилися з порядком операцій. Було відзначено, що перед множенням і діленням ми вставимо ще одну операцію. Ми можемо це зробити зараз.

Порядок операцій

Виконайте всі операції всередині угруповання символів, починаючи з самого внутрішнього набору.
Виконуйте всі експоненціальні операції, коли ви підходите до них, рухаючись зліва направо.
Виконуйте всі множення і ділення, як ви підходите до них, рухаючись зліва направо.
Виконуйте всі додавання і віднімання, як ви підходите до них, рухаючись зліва направо.

Набір зразків D

Скористайтеся порядком операцій, щоб спростити кожну з наступних дій.

Приклад$\PageIndex{11}$

$2^2 + 5 = 4 + 5 = 9$

Приклад$\PageIndex{12}$

$5^2 + 3^2 + 10 = 25 + 9 + 10 = 44$

Приклад$\PageIndex{13}$

\ (
\ почати {вирівняний}
2^ {2} + (5) (8) -1 &=4+ (5) (8) -1\\
&=4+40-1\\
&=43
\ кінець {вирівняний}
\)

Приклад$\PageIndex{14}$

\ (
\ почати {вирівняний}
7\ cdot 6-4^ {2} +1^ {5} &= 7\ cdot 6-16+1\\
&= 42-16+1\\
&=27
\ кінець {вирівняний}
\)

Приклад$\PageIndex{15}$

\ (
\ почати {вирівняний}
(2+3) ^ {3} +7^ {2} -3 (4+1) ^ {2} & =( 5) ^ {3} +7^ {2} -3 (5) ^ {2}\
&=125+49-3 (25)\\
&=125+49-75
\ кінець {вирівняний}
\)

Приклад$\PageIndex{16}$

\ (
\ почати {вирівняний}
\ ліворуч [4 (6+2) ^ {3}\ праворуч] ^ {2} &=\ ліворуч [4 (8) ^ {3}\ праворуч] ^ {2}\
&= [4 (512)] ^ {2}\
&= [2048] ^ {2}\
&= 4,194,304
\ кінець {вирівняний}
\)

Приклад$\PageIndex{17}$

\ (
\ почати {вирівняний}
6\ ліворуч (3^ {2} +2^ {2}\ праворуч) +4^ {2} &=6 (9+4) +4^ {2}\
&=6 (13) +4^ {2}\
&=6 (13) +16\\
&=78+16\\
&=94
\ кінець {вирівняний}
\)

Приклад$\PageIndex{18}$

\ (
\ почати {вирівняний}
\ dfrac {6^ {2} +2^ {2}} {4^ {2} +6\ cdot 2^ {2}} +\ dfrac {1^ {3} +8^ {2}} {10^ {2} - (19) (5)} &=\ dfrac {36+4} {16+6\ cdot 4} +\ dfrac {1+64} {100-95}\\
&=\ dfrac {36+4} {16+24} +\ dfrac {1+64} {100-95}\
&=\ dfrac {40} +\ dfrac {65} {5}\\
&=1+13\\
&=14
\ кінець {вирівняний}
\)

Практика Set D

Скористайтеся порядком операцій, щоб спростити наступне.

Завдання практики$\PageIndex{8}$

$3^2 + 4 \cdot 5$

Відповідь: 29

Завдання практики$\PageIndex{9}$

$2^3 + 3^3 - 8 \cdot 4$

Відповідь: 3

Завдання практики$\PageIndex{10}$

$1^4 + (2^2 + 4)^2 \div 2^3$

Відповідь: 9

Завдання практики$\PageIndex{11}$

$[6(10 - 2^3)]^2 - 10^2 - 6^2$

Відповідь: 8

Завдання практики$\PageIndex{12}$

$\dfrac{5^2 + 6^2 - 10}{1 + 4^2} + \dfrac{0^4 - 0^5}{7^2 - 6 \cdot 2^3}$

Відповідь: 3

Вправи

Для наступних задач запишіть кожну з величин, використовуючи експоненціальні позначення.

Вправа$\PageIndex{1}$

$b$до четвертого

Відповідь: $b^4$

Вправа$\PageIndex{2}$

$a$в квадраті

Вправа$\PageIndex{3}$

$x$до восьмого

Відповідь: $x^8$

Вправа$\PageIndex{4}$

$(-3)$кубічний

Вправа$\PageIndex{5}$

$5$разів у$s$ квадраті

Відповідь: $5s^2$

Вправа$\PageIndex{6}$

$3$в квадраті разів$y$ до п'ятого

Вправа$\PageIndex{7}$

$a$куб мінус в$(b + 7)$ квадраті

Відповідь: $a^3 - (b + 7)^2$

Вправа$\PageIndex{8}$

$(21 - x)$$x + 5$кубик плюс до сьомого

Вправа$\PageIndex{9}$

$xxxxx$

Відповідь: $x^5$

Вправа$\PageIndex{10}$

$(8)(8)xxxx$

Вправа$\PageIndex{11}$

$2 \cdot 3 \cdot 3 \cdot 3 \cdot 3xxyyyyy$

Відповідь: $2(3^4)x^2y^5$

Вправа$\PageIndex{12}$

$2 \cdot 2 \cdot 5 \cdot 6 \cdot 6 \cdot 6xyyzzzwwww$

Вправа$\PageIndex{13}$

$7xx(a + 8)(a + 8)$

Відповідь: $7x^2(a + 8)^2$

Вправа$\PageIndex{14}$

$10xyy(c + 5)(c + 5)(c + 5)$

Вправа$\PageIndex{15}$

$4x4x4x4x4x$

Відповідь: $(4x)^5$або$4^5x^5$

Вправа$\PageIndex{16}$

$(9a)(9a)(9a)(9a)$

Вправа$\PageIndex{17}$

$(-7)(-7)(-7)aabbba(-7)baab$

Відповідь: $(-7)^4a^5b^5$

Вправа$\PageIndex{18}$

$(a - 10)(a - 10)(a + 10)$

Вправа$\PageIndex{19}$

$(z + w)(z + w)(z + w)(z - w)(z - w)$

Відповідь: $(z + w)^3(z - w)^2$

Вправа$\PageIndex{20}$

$(2y)(2y)2y2y$

Вправа$\PageIndex{21}$

$3xyxxy - (x + 1)(x + 1)(x + 1)$

Відповідь: $3x^3y^2 - (x + 1)^3$

Для наступних проблем розгорніть величини, щоб не з'являлися показники.

Вправа$\PageIndex{22}$

$4^3$

Вправа$\PageIndex{23}$

$6^2$

Відповідь: $6 \cdot 6$

Вправа$\PageIndex{24}$

$7^3y^2$

Вправа$\PageIndex{25}$

$8x^3y^2$

Відповідь: $8 \cdot x \cdot x \cdot x \cdot y \cdot y$

Вправа$\PageIndex{26}$

$(18x^2y^4)^2$

Вправа$\PageIndex{27}$

$(9a^3b^2)^3$

Відповідь: $(9aaabb)(9aaabb)(9aaabb)$або$9 \cdot 9 \cdot 9aaaaaaaaabbbbbb$

Вправа$\PageIndex{28}$

$5x^2(2y^3)^3$

Вправа$\PageIndex{29}$

$10a^3b^2(3c)^2$

Відповідь: $10aaabb(3c)(3c)$або$10 \cdot 3 \cdot 3aaabbcc$

Вправа$\PageIndex{30}$

$(a + 10)^2(a^2 + 10)^2$

Вправа$\PageIndex{31}$

$(x^2 - y^2)(x^2 + y^2)$

Відповідь: $(xx - yy)(xx + yy)$

Для наведених нижче проблем виберіть число (або цифри), щоб показати, що

Вправа$\PageIndex{32}$

$(5x)^2$взагалі не дорівнює$5x^2$.

Вправа$\PageIndex{33}$

$(7x)^2$як правило, не дорівнює$7x^2$

Відповідь: Виберіть$x = 2$. Потім,$196 \not = 28$

Вправа$\PageIndex{34}$

$(a + b)^2$як правило, не дорівнює$a^2 + b^2$

Вправа$\PageIndex{35}$

Для чого дійсне число$(6a)^2$ дорівнює$6a^2$

Відповідь: $0$

Вправа$\PageIndex{36}$

Для чого дійсні числа$b$,$a$ і,$(a + b)^2$ дорівнює$a^2 + b^2$.

Використовуйте порядок операцій, щоб спростити величини для наступних завдань.

Вправа$\PageIndex{37}$

$3^2 + 7$

Відповідь: $16$

Вправа$\PageIndex{38}$

$4^3 - 18$

Вправа$\PageIndex{39}$

$5^2 + 2(40)$

Відповідь: $105$

Вправа$\PageIndex{40}$

$8^2 + 3 + 5(2 + 7)$

Вправа$\PageIndex{41}$

$2^5 + 3(8 + 1)$

Відповідь: $59$

Вправа$\PageIndex{42}$

$3^4 + 2^4(1 + 5)^3$

Вправа$\PageIndex{43}$

$(6^2 - 4^2) \div 5$

Відповідь: $4$

Вправа$\PageIndex{44}$

$2^2(10 - 2^3)$

Вправа$\PageIndex{45}$

$(3^4 - 4^3) \div 17$

Відповідь: $1$

Вправа$\PageIndex{46}$

$(4 + 3)^2 + 1 \div (2 \cdot 5$

Вправа$\PageIndex{47}$

$(2^4 + 2^5 - 2^3 \cdot 5)^2 \div 4^2$

Відповідь: $4$

Вправа$\PageIndex{48}$

$1^6 + 0^8 + 5^2(2 + 8)^3$

Вправа$\PageIndex{49}$

$(7)(16) - 9^2 + 4(1^1 + 3^2)$

Відповідь: $71$

Вправа$\PageIndex{50}$

$\dfrac{2^3 - 7}{5^2}$

Вправа$\PageIndex{51}$

$\dfrac{(1 + 6)^2 + 2}{19}$

Відповідь: $\dfrac{51}{19}$

Вправа$\PageIndex{52}$

$\dfrac{6^2 - 1}{5} + \dfrac{4^3 + (2)(3)}{10}$

Вправа$\PageIndex{53}$

$\dfrac{(2 + 1)^3 + 2^3 + 1^3}{6^2} - \dfrac{15^2 - [2(5)]^2}{5 \cdot 5^2}$

Вправа$\PageIndex{54}$

$\dfrac{6^3 - 2 \cdot 10^2}{2^2} + \dfrac{18(2^3 + 7^2)}{2(19) - 3^3}$

Відповідь: $\dfrac{1070}{11}$або$97.27$

Вправи для огляду

Вправа$\PageIndex{55}$

Використовуйте алгебраїчні позначення, щоб написати твердження «число, розділене на вісім, плюс п'ять, дорівнює десяти».

Вправа$\PageIndex{56}$

Намалюйте числовий рядок, що простягається від −5 до 5, і розмістіть точки на всіх дійсних числах, які строго більші за −3, але менші або рівні 2.

Відповідь: $clipboard_efe9b717158f5efe402d1ea75b9fc0430.png$

Вправа$\PageIndex{57}$

Кожне ціле число є цілим числом?

Вправа$\PageIndex{58}$

Використовуйте комутативну властивість множення, щоб записати число, рівне числу$yx$.

Відповідь: $xy$

Вправа$\PageIndex{59}$

Використовуйте властивість distributive для розширення$3(x+6)$.

Приклад\(\PageIndex{1}\)

Експоненціальне позначення

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\)

Приклад\(\PageIndex{8}\)

Приклад\(\PageIndex{9}\)

Приклад\(\PageIndex{10}\)

Порядок операцій

Приклад\(\PageIndex{11}\)

Приклад\(\PageIndex{12}\)

Приклад\(\PageIndex{13}\)

Приклад\(\PageIndex{14}\)

Приклад\(\PageIndex{15}\)

Приклад\(\PageIndex{16}\)

Приклад\(\PageIndex{17}\)

Приклад\(\PageIndex{18}\)