Передмова
- Page ID
- 58591
Передмова
Елементарна алгебра - це робочий текст, який охоплює традиційні теми, що вивчаються в сучасному курсі елементарної алгебри. Він призначений для студентів, які:
- Цей текст можна використовувати в стандартних лекційних або самостійних заняттях. Щоб допомогти учням досягти цих цілей і зробити вивчення алгебри приємним і корисним досвідом, Елементарна алгебра організована наступним чином.
педагогічні особливості
- Цілі
Набори зразків
Елементарна алгебра містить приклади, які задаються в коробках для зручності довідки. Приклади називаються наборами зразків з двох причин:
- Паралельний набір практик слідує за кожним набором зразків, який підсилює щойно вивчені поняття. Відповіді на всі набори практик відображаються з питанням при перегляді цього вмісту в Інтернеті або в кінці глави в друкованій версії.
Розділ вправи
Проблеми парні так, що непарні проблеми еквівалентні за своїм виглядом і труднощами парним задачам. Відповіді на непарні задачі надаються з вправою при перегляді онлайн, або в задній частині глави в друкованому варіанті.
Вправи для огляду
Цей розділ складається з проблем, які формують сукупний огляд матеріалу, висвітленого в попередніх розділах тексту, і не обмежується матеріалами цього розділу. Вправи наведені за розділами для зручності довідки.
Короткий зміст ключових понять
Короткий зміст важливих ідей та формул, що використовуються протягом усього розділу, міститься в кінці кожної глави. Більше, ніж просто список термінів, резюме є цінним інструментом, який підсилює концепції при підготовці до іспиту на знання в кінці глави, а також майбутніх іспитів. Резюме вводить кожен пункт до розділу тексту, де він обговорюється.
Доповнення до вправ
На додаток до численних вправ розділу, кожна глава включає приблизно 100 додаткових проблем, на які посилається розділ. Відповіді на непарні проблеми включаються з проблемами при перегляді онлайн і в задній частині глави в друкованому варіанті.
Іспит з кваліфікації
Кожна глава закінчується іспитом на знання, який може служити оглядом глави або оцінкою глави. Іспит на знання є ключовим до розділів, що дозволяє студенту повернутися до тексту для допомоги. Відповіді на всі проблеми іспиту з кваліфікації включені в вправи при перегляді в Інтернеті, або в задній частині глави в друкованій версії.
Контент
Стиль письма неформальний і доброзичливий, пропонуючи безглуздий, простий підхід до алгебри. Ми доклали навмисних зусиль, щоб не писати інший текст, який мінімізує використання слів, тому що ми вважаємо, що студенти можуть вивчати алгебраїчні поняття та розуміти алгебраїчні прийоми, використовуючи слова та символи, а не лише символи. Наш досвід показує, що студенти на початковому рівні недостатньо досвідчені з математикою, щоб зрозуміти лише символічні пояснення; їм також потрібно прочитати пояснення.
Ми дуже подбали про те, щоб представити концепції та прийоми, щоб вони були зрозумілі та легко запам'ятовуються. Після того як концепції були розроблені, учнів попереджають про поширені підводні камені.
Арифметичний огляд
Цей розділ містить безліч прикладів арифметичних прийомів, які прямо або опосередковано використовуються в алгебрі. Оскільки глава призначена як огляд, методи вирішення проблем представлені без розробки. Тому не передбачено жодного робочого простору, а також глава не містить всіх педагогічних особливостей тексту. Як огляд, ця глава може бути призначена на розсуд інструктора, а також може бути цінним довідковим інструментом для учня.
Основні властивості дійсних чисел
Символи, позначення та властивості чисел, що становлять основу алгебри, а також показники та правила показників, введені в Основні властивості дійсних чисел. Кожне властивість дійсних чисел і правила показників виражаються як символічно, так і буквально. Буквальні пояснення включені, оскільки лише символічні пояснення можуть бути важко інтерпретувати студенту.
Основні операції з дійсними числами
Основні операції з дійсними числами представлені в цьому розділі. Поняття абсолютної величини обговорюється як геометрично, так і символічно. Геометрична презентація пропонує візуальне розуміння значення х. Символічна презентація включає в себе буквальне пояснення того, як використовувати визначення. Негативні показники розробляються, використовуючи взаємні та правила показників, які студент вже вивчив. Наукові позначення також включені, використовуючи унікальні та реальні приклади.
Алгебраїчні вирази та рівняння
Операції з алгебраїчними виразами та числовими оцінками введені в алгебраїчні вирази та рівняння. Коефіцієнти описуються, а не просто визначені. Спеціальні біноміальні продукти мають як буквальне символічне пояснення, і оскільки вони трапляються так часто в математиці, ми були обережні, щоб допомогти студенту запам'ятати їх. У кожному прикладі завдання школяра «розмовляють» через символічну форму.
Розв'язування лінійних рівнянь та нерівностей
У цьому розділі акцент робиться на механіці розв'язання рівнянь, яка чітко пояснює, як виділити змінну. Мета полягає в тому, щоб допомогти студенту відчувати себе більш комфортно при вирішенні прикладних завдань. Для студента передбачена широка можливість практикувати переклад слів на символи, що є важливою частиною «П'ятикрокового методу» вирішення прикладних завдань (розглянуто в розділі 5.6 та розділі 5.7).
Факторингові поліноми
Факторинг є важливим навиком для успіху в курсах алгебри та математики вищого рівня. Тому ми подбали про розвиток розуміння студентом процесу факторизації. Методика послідовно ілюструється відображенням порожнього набору дужок та описом розумового процесу, який використовується для виявлення термінів, які повинні бути розміщені всередині дужок.
Схема факторингу спеціальних виробів представлена як словесними, так і символічними описами, так як не всі студенти можуть інтерпретувати символічні описи поодинці. Для факторингу триноміалів з провідними коефіцієнтами, відмінними від 1, представлені дві методики, стандартний метод «проб і помилок» та метод «збирати та відкинути» (метод, подібний до методу «ac»).
Графічні лінійні рівняння та нерівності в одній та двох змінних
У цьому розділі студенту показано, як графіки надають інформацію, яка не завжди очевидна лише з рівняння. Розділ починається з встановлення зв'язку між змінними у рівнянні, кількістю осей координат, необхідних для побудови графіка, та просторовою розмірністю як системи координат, так і графіка. Інтерпретація графіків також підкреслюється по всій главі, починаючи з побудови точок. Формула нахилу повністю розроблена, прогресуючи від словесних фраз до математичних виразів. Потім вирази формуються у рівняння, прямо вказуючи, що співвідношення - це порівняння двох величин одного типу (наприклад, відстані, ваги або грошей). Такий підхід приносить користь студентам, які проходять майбутні курси, які використовують графіки для відображення інформації.
Студенту показано, як графувати лінії, використовуючи метод перехоплення, табличний метод та метод нахилу-перехоплення, а також як розрізнити, шляхом огляду, косі та горизонтальні/вертикальні лінії.
Раціональні вирази
Детальне вивчення арифметичних операцій з раціональними виразами представлено в цьому розділі, починаючи з визначення раціонального виразу і потім переходячи відразу до обговорення області. Також включено процес зменшення раціонального вираження та ілюстрації множення, ділення, додавання та віднімання раціональних виразів. Так як операції додавання і віднімання можуть викликати найбільшу складність, їм приділяється особлива увага. Ми намагалися зробити письмове пояснення прикладів зрозумілішим, використовуючи підхід «заморожування кадру».
П'ятиступінчастий метод розв'язання прикладних задач включений в цю главу, щоб показати підхід до вирішення проблем числення, робочих задач та задач геометрії. У розділі також ілюструється спрощення складних раціональних виразів за допомогою методу комбінувати-ділення та методу LCD-множинного поділу.
Коріння, радикали та рівняння квадратного кореня
Проводиться відмінність між головним квадратним коренем числа x
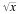 , і вторинним квадратним коренем числа
x
, і вторинним квадратним коренем числа
x
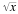 , поясненням і прикладом. Спрощення радикальних виразів, які як включають, так і не включають дроби, показано на багатьох детальних прикладах; після цього слід пояснення того, як і чому радикали усуваються зі знаменника радикального виразу. Були включені реальні застосування радикальних рівнянь, такі як проблеми, пов'язані з добовим виходом, щоденними продажами, частотою електронного резонансу та кінетичною енергією.
, поясненням і прикладом. Спрощення радикальних виразів, які як включають, так і не включають дроби, показано на багатьох детальних прикладах; після цього слід пояснення того, як і чому радикали усуваються зі знаменника радикального виразу. Були включені реальні застосування радикальних рівнянь, такі як проблеми, пов'язані з добовим виходом, щоденними продажами, частотою електронного резонансу та кінетичною енергією.Квадратні рівняння
Обговорюються методи розв'язання квадратичних рівнянь, а також логіка, що лежить в основі кожного методу. Ретельно розробляються факторинг, видобуток коренів, заповнення квадрата, квадратична формула. Повторно введено властивість нульового фактора дійсних чисел. Глава також включає графіки квадратичних рівнянь на основі стандартної параболи, y = x 2 , і прикладні задачі з областей виробництва, населення, фізики, геометрії, математики (число і томів), і астрономії, які вирішуються за допомогою п'ятиступеневого методу.
Системи лінійних рівнянь
Починаючи з графічного рішення систем, цей розділ включає інтерпретацію незалежних, суперечливих та залежних систем та приклади для ілюстрації застосувань цих систем. Пояснено метод заміщення та метод додавання рішення системи шляхом елімінації, зазначаючи, коли використовувати кожен метод. П'ятиступінчастий метод знову використовується для ілюстрації розв'язків ціннісних і курсових задач (задач монети і суміші), використовуючи креслення, які відповідають фактичному рішенню.
- Паралельний набір практик слідує за кожним набором зразків, який підсилює щойно вивчені поняття. Відповіді на всі набори практик відображаються з питанням при перегляді цього вмісту в Інтернеті або в кінці глави в друкованій версії.
- Цілі
