7.4: Рівняння ван дер Ваальса
- Page ID
- 29192
Незважаючи на те, що ван дер Ваальс EOS (VdW EOS) існує вже більше ста років, ми все ще визнаємо досягнення ван дер Ваальса як вирішальні для революції нашого мислення про EOS. Ми говоримо про VdW EOS з педагогічних причин, а не тому, що вона знаходить будь-яке практичне застосування в сучасному світі. Насправді VdW EOS не використовується для будь-яких практичних дизайнерських цілей. Однак більшість EOS, широко використовуваних сьогодні для практичних цілей дизайну, були отримані від VdW EOS.
Внесок VdW EOS можна підсумувати наступним чином:
- Це радикально покращило прогнозну здатність порівняно з ідеальним газом EOS,
- Це було першим, хто спрогнозував безперервність речовини між газом і рідиною,
- Він сформулював Принцип відповідних держав (PCS),
- Вона заклала основи для сучасних кубічних ЕОС.
У своїй кандидатській дисертації в 1873 році ван дер Ваальс запропонував напівемпірично усунути основні ключові «слабкі місця», які мала з собою ідеальна ЕОС. По суті, те, що він зробив, - це знову подивитися на основні припущення, які лежать в основі ідеального EOS, який ми перерахували вище.
VdW припадає на ненульовий молекулярний об'єм і ненульову силу тяжіння реальної речовини. Він зрозумів, що є точка, при якій об'ємом, займаним молекулами, не можна нехтувати. Одне з перших речей, які визнали VdW, - це те, що молекули повинні мати кінцевий об'єм, і цей обсяг повинен бути відніманий з обсягу контейнера. У той же час він змінив термін тиску, щоб визнати той факт, що молекули взаємодіють один з одним, хоча згуртовані сили. Це два основних цінних визнання, які він ввів.
Ідеальний EOS зазначає:
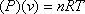(7.5)
або,
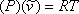(7.6)
де
представляють молярний об'єм (
) речовини.
VdW зосередив свою увагу на зміні термінів «P» і «v» в початковому законі ідеального газу шляхом введення відповідної корекції. Озираючись на нерівність рівняння (6.4) у модулі 6, VdW припустив, що різниця обох тисків є результатом сили тяжіння - сили зчеплення - нехтуються в ідеальній моделі (рівняння 7.6) і, таким чином,
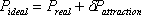(7.7)
У цей момент VdW постулював термін ΔpAttraction, обернену функцію середньої відстані між молекулами — це є прямим наслідком закону Ньютона інерційних сил тяжіння, F α (відстань) -2. Визнаючи, що обсяг газу є мірою середньої відстані між молекулами (чим менше обсяг, тим ближче молекули і навпаки),
(7.8)
і використовуючи «а» як константу пропорційності,
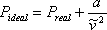(7.9)
Далі VdW подбав про нерівність у рівнянні (6.5) (див. Модуль 6). Будь-яка частинка займає фізичний простір; отже, простір, доступне газу, менше, ніж загальний обсяг його контейнера. Скажімо, ми можемо експериментально визначити фактичний фізичний простір, який займають всі молекули в контейнері, і що ми називаємо його «b», або спільним томом. VdW тоді запропонував:
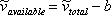(7.10)
Включення параметра «b» (со-том) визнає роль сил відштовхування. Сили відштовхування заважають молекулам «руйнувати» один одного, не даючи їм підійти занадто близько. У конденсованому стані спостерігається максимально допустима «близькість» серед молекул. Тому саме через сили відштовхування ми не можемо стиснути об'єм рідини за межі її співоб'ємного значення «b». Якщо молекули наближаються занадто близько один до одного, сили відштовхування беруть на себе, щоб запобігти їх самознищення.
Підсумовуючи, VdW запропонував коригувати умови тиску та об'єму ідеальної моделі, представленої рівнянням (7.6). «Новим» модифікованим ідеальним рівнянням стану стає:
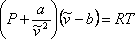(7.11а)
або,
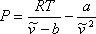(7.11b)
де:
P = абсолютний тиск
v = молярний об'єм
T = абсолютна температура
R = універсальна газова постійна
Рівняння (7.11b) демонструє, що VdW EOS є явним у тиску. На цьому етапі важливо підкреслити, що будь-яке прогнозування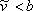
з рівнянь (7.11) безглуздо через фізичної значущості, яку ми надали цьому параметру. Оскільки всі інші параметри є константами, рівняння (7.11) є функціональними зв'язками змінних P, T і
:
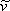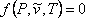(7.12)
Тому рівняння (7.11a) виражає зв'язок PVT і, отже, це рівняння стану. У цьому рівнянні «a» і «b» є константами, характерними для кожного компонента. Однак числове значення «R» залежить від системи обраних одиниць, про що ми говорили вище.
Настав час задати собі дуже важливе питання:
Як ми обчислюємо «а» і «б» для кожної речовини?
Як можна зробити висновок з їх визначень, «а» і «б» різні для різних речовин; т. Е.
;
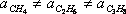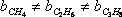
Як ми відносимо «а» і «б» з відомими і легкодосяжними фізичними властивостями речовин?
Виявляється, існує сукупність умов, званих умовами критичності, які повинні бути виконані для всіх систем, за умови, що ці системи задовольняють 2-му закону термодинаміки. Дійсно, в попередньому розділі ми визнали, що критична ізотерма чистої речовини має точку перегину (зміни кривизни) в критичній точці. Крім того, ми визнали критичну точку максимальною точкою (вершиною) оболонки P-V. Ця умова горизонтального згинання критичної ізотерми в критичній точці математично нав'язується виразом:
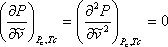(7.13)
Ці умови називаються умовами критичності. Виходить, що при накладанні цих умов на рівняння (7.11a) можна вивести вирази для параметрів «a» і «b» як функції критичних властивостей наступним чином:
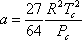(7.14а)
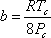(7.14 б)
Можливо, ви захочете довести це як вправу. Тому «a» і «b» можуть бути відомі, оскільки вони є функціями відомих (табличних) властивостей всіх речовин, що цікавлять (критичний тиск і температура).
Поки що ми застосували VdW EOS до чистих компонентів. Чи можемо ми екстраполювати це, щоб застосувати до багатокомпонентних систем?
Щоб розширити цю концепцію на систему з більш ніж одного компонента, ми використовуємо те, що називається правилом змішування. Правило змішування пов'язує параметри, що характеризують суміш (a m і b m) з окремими внесками чистих компонентів, що входять до складу цієї суміші (a i і b i)
Як нам це зробити? VdW запропонував зважити внесок кожного компонента з використанням їх мольних композицій, наступним чином:
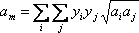(7.15 а)
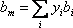(7.15 б)
Перше називається правилом квадратичного змішування, тоді як друге відоме як правило лінійного змішування.