Skip to main content
LibreTexts - Ukrayinska

6.3: Ідеальна поведінка

  1. Last updated
  2. Save as PDF
  • Page ID
    29264

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ідеальний газ - уявний газ, який задовольняє таким умовам:

    • Незначні взаємодії між молекулами,
    • Його молекули не займають обсягу (мізерно малий молекулярний об'єм),
    • Зіткнення між молекулами ідеально еластичні — це означає, що ніяка енергія не втрачається після зіткнення.

    Ми визнаємо, що ця рідина є уявною, оскільки - строго кажучи - ідеальних газів немає. У будь-якій рідині всі молекули в якійсь мірі притягуються одна до одної. Однак ідеальне наближення найкраще працює при деяких граничних умовах, де сили тяжіння можна вважати слабкими. Насправді до ідеальної поведінки можуть наблизитися реальні гази при низькому тиску (близькому до атмосферного) та високих температурах. Відзначимо, що при низьких тисках і високих температурах відстань між будь-якою парою молекул газу велике. Оскільки сили тяжіння слабшають з відстанню, ми вибрали умову, коли сили тяжіння можна знехтувати. На закінчення розглянемо газовий ідеал, коли кожна молекула поводиться так, ніби вона одна — молекули настільки далеко один від одного, що на них не впливає існування інших молекул.

    Поведінка ідеальних газів вивчено вичерпно і може бути широко описана математичними співвідношеннями.

    Для заданої маси ідеального газу обсяг обернено пропорційний тиску при постійній температурі, т. Е.

    \[ v\alpha\frac{1}{P} (at\,constant\,temperature) \label{Boyle} \]

    Цей зв'язок відомий як Закон Бойла. Крім того, обсяг прямо пропорційний температурі, якщо тиск підтримується постійним, т. Е.

    \[ v\alpha T (at\,constant\,pressure) \label{Charles} \]

    Цей зв'язок відомий як Закон Чарльза. Поєднуючи обидва закони і визнаючи «R» (універсальну газову константу) постійною пропорційності, ми отримуємо дуже звичне рівняння:

    \[ Pv = nRT \label{EOS} \]

    Це являє собою рівняння стану (EOS) ідеального газу. Чисельні значення «R» залежать від системи одиниць, яка використовується:

    \[ R = 10.731\dfrac{psia ft^3}{lbmol R} = 8.3144\dfrac{Joule}{gmole K} = 1.9872\dfrac{cal}{gmole K} \nonumber \]

    \[ R = 1.314\dfrac{atm ft^3}{lbmol K} = 0.7302\dfrac{atm ft^3}{lbmol R} = 1.9869\dfrac{BTU}{lbmol R} \nonumber \]

    Якщо побудувати діаграму p-v для ідеального газу при заданій температурі, то в кінцевому підсумку вийде ізотерма, показана на малюнку 6.3.2.

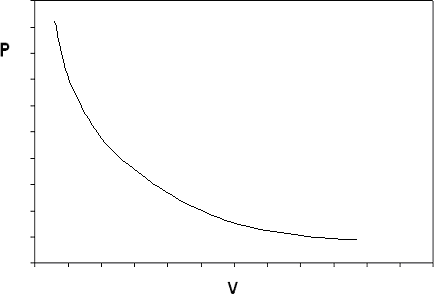
    Зверніться до інструктора, якщо ви не можете побачити або інтерпретувати цю графіку.
    Малюнок\(\PageIndex{2}\): Ізотерма P-v для ідеального газу

    Ідеальна газова модель передбачає дві обмежувальні поведінки рідини: по-перше, об'єм газу стає дуже великим при дуже низькому тиску (\( v \rightarrow \infty \)як концепція\( P \rightarrow 0 \), яка узгоджується з тим, що ми знаємо з нашого досвіду у фізичному світі). І по-друге,\( v \rightarrow \infty \) як\( P \rightarrow 0 \) (обсяг матерії просто «зникає», якщо тиск досить високий: це поняття ми б не були так готові прийняти). Ці дві поведінки є наслідком припущень, зроблених в ідеальній моделі газу.