4.1: Бінарні системи

Last updated
Save as PDF

Page ID: 29110

Michael Adewumi
Pennsylvania State University via John A. Dutton: e-Education Institute

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Поки що ми зосередили свою увагу на однокомпонентних системах (також званих унарними, однокомпонентними або чистокомпонентними системами). Однак реальні системи ніколи не є однокомпонентними; це багатокомпонентні системи. Найпростіша з цієї категорії - двійкова система. Хороша новина, однак, полягає в тому, що поведінка багатокомпонентних систем досить схожа на поведінку бінарних систем. Тому зупинимося на бінарних системах, так як їх простіше проілюструвати.

Помістимо два гази (А і В) в ізотермічну комірку. Як ми робили раніше, ми будемо підтримувати постійну температуру під час цього експерименту (показано на рис.4.1.1)

Дивіться текст вище і нижче зображення — Малюнок\(\PageIndex{1}\): Ізотермічний експеримент

Якщо ми рухаємо поршень вниз, ми стискаємо гази, викликаючи зменшення обсягу. При такому розкладі відбудеться підвищення тиску. Процес починається в точці А, як показано на малюнку 4.1.2, умова повного пара.

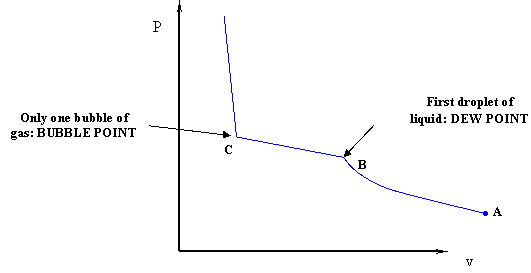
Нічого тут не є новим щодо стиснення самої пари. Зі збільшенням тиску відповідно зменшується обсяг. Після деякого стиснення з'явиться перша крапелька рідини. Тобто ми знайшли точку роси суміші (точка В). Потім приступаємо до стиснення. У міру подальшого стиснення системи буде з'являтися більше рідини і обсяг буде продовжувати зменшуватися.

Здавалося б, ми бачимо тут ті ж особливості, що і у однокомпонентної системи, яку ми вивчали в попередніх модулів. Але почекайте хвилинку, це так?

Власне, різниця є. Під час фазового переходу тиск не залишається постійним в цьому експерименті. Насправді, коли стиснення прогресує і утворюється більше рідини, тиск продовжує зростати - хоча і не так різко, як в однофазній парній області. Коли вся система стала рідкою, залишилася лише нескінченно мала бульбашка пари, ми знаходимося в точці С - точці бульбашки суміші. Зверніть увагу, що для бінарних сумішей (як у випадку з багатокомпонентними сумішами) точка роси і точка бульбашки не виникають при однаковому тиску для ізотермічного стиснення. Якщо згадати, для однокомпонентної системи точка роси і точка бульбашки збігаються. Це не вірно для двійкових і багатокомпонентних систем. Порівняйте малюнок 4.1.2 з малюнком 3.2.4 (повторюється нижче з модуля 3), щоб побачити цю точку.

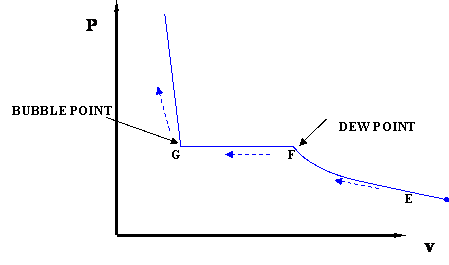
Переглянути текст, що оточує зображення — Малюнок\(\PageIndex{2}\) (повторюється): Діаграма p-v для бінарної суміші

ЧОМУ?? Чому підвищується тиск під час фазового переходу? У цей момент ми починаємо усвідомлювати способи, якими склад відіграє фундаментальну роль у поведінці сумішей.

В однокомпонентної системі і рідина, і пара в двофазної області мають однаковий склад (всередині системи є тільки одне хімічна речовина). Зараз, коли суміш існує в двофазному стані, присутні різні молекули різних видів і вони можуть перебувати як в рідкому, так і пароподібному стані (двофазний стан). Деякі з них «воліють» перебувати в газовій фазі, а інші «воліють» перебувати в рідкій фазі. Це «перевагу» контролюється волатильністю даного компонента. Коли ми досягаємо точки В (рис. 4.1.2) і з'являється перша крапля рідини, найважчі молекули - це ті, які переважно переходять до цієї першої крихітної крапельки рідкої фази. Для «важких» молекул, враховуючи вибір, бажано перебувати в конденсованому стані.

Оскільки ми продовжуємо утворювати більше рідини (стисненням), в основному легкі молекули залишаються в паровій фазі. Однак в кінцевій точці переходу (точка С на рис. 4.1.2) ми змусили всіх перейти в рідкий стан — у них більше немає вибору. Це примусове виконання вимагає більшого тиску. Якщо порівняти зразок рідини в умовах точки роси (точка В на рис. 4.1.2) з зразком, взятим в середині переходу, то зрозуміло, що перший був би багатшим важкими компонентами, ніж другий. Властивості найважчого компонента були б найбільш впливовими в точці роси (коли вперше з'являється рідина); тоді як властивості більш легкого компонента будуть найбільш впливовими в точці міхура (коли останній міхур ось-ось зникне.)

У двофазної області тиск збільшується в міру проходження системи від точки роси до точки міхура. Склад рідини і пари змінюється; але — будьте уважні! — загальна композиція завжди однакова! У точці роси склад пари дорівнює загальному складу системи; однак нескінченно мала кількість рідини, яка конденсується, багатша менш летючим компонентом. У точці міхура склад рідини дорівнює складу системи, але нескінченно мала кількість пари, що залишається в точці міхура, багатша більш летючим компонентом, ніж система в цілому.

Взагалі, коли два різні види змішуються, деякі види поведінки окремих видів та їх властивості зміняться. Їх звичайна поведінка (як чисті компоненти) буде змінено як наслідок створеного нового поля молекулярних взаємодій. Перебуваючи в чистому стані, молекули взаємодіють лише з подібними молекулами. З іншого боку, в суміші відбуваються нові взаємодії між різнорідними молекулами.

Наш наступний крок, щоб продовжити цю дискусію послідовно, полягає в тому, щоб намалювати повну діаграму P-V для цієї бінарної суміші шляхом окреслення двофазної області. Точно так само, як ми робили раніше, окреслюємо двофазну область, намалювавши повне сімейство ізотерм на діаграмі P-V. Малюнок 4.1.3 ілюструє це.

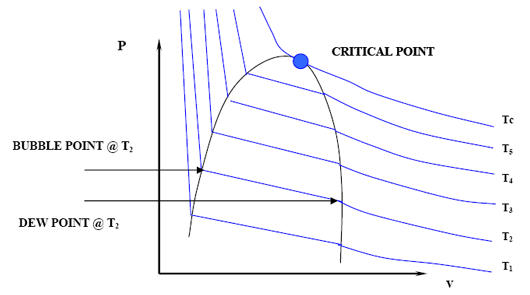
Дивіться текст над зображенням — Малюнок\(\PageIndex{3}\): Сімейство ізотерм на діаграмі P-V Бінарна суміш

Знову ж таки, лінія, що з'єднує всі точки міхура та роси, буде генерувати криву міхура та точки роси, обидві з яких зустрічаються у критичній точці. Зверніть увагу, що критична точка не представляє максимуму на P-V діаграмі суміші. Також зверніть увагу, що тиск точки міхура та тиск точки роси вже не однакові.

Знову ж таки, ізотерми через двофазну область не горизонтальні, а мають певний нахил. Це повинно мати підтекст. Насправді, це так і є. Що робити, якщо ми зараз хочемо побудувати діаграму P-T для цієї суміші? Чи буде у нас тільки одна лінія, де криві міхура і точки роси лежать один на одному, як це було для однокомпонентної системи? Звичайно, ні. Замість того, щоб обидві криві були разом, крива точки міхура зміститься вліво вгорі (більш високий тиск), а крива точки роси зміститься в нижнє праворуч (нижній тиск) - обидва вони зустрічаються в критичній точці. На малюнку 4.1.4 показана типова фазова оболонка для суміші.

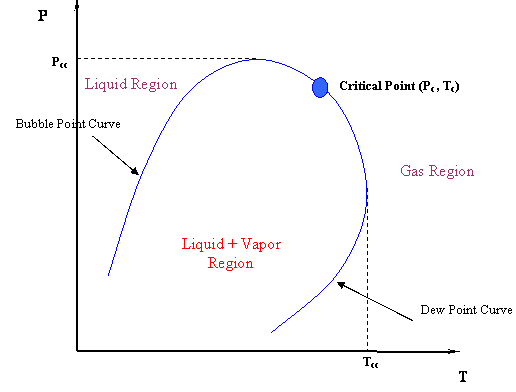
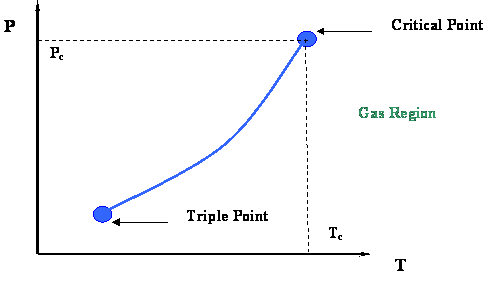
Зверніть увагу на величезну різницю між P-T кривої багатокомпонентної системи (двійкова система в даному випадку, рис. 4.1.4) і кривою P-T чистої (одиночної) складової (рис. 3.1.1 модуля 3, повторюється нижче). Єдина система, для якої крива точки міхура буде збігатися з кривою точки роси, - це однокомпонентна система, де ми маємо єдину лінію для діаграми P-T (наприклад, крива точки кипіння, представлена на рис.3.1.1). На рис. 3.1.1 критична точка являє собою максимальну сукупність (P, T) значень, які ви могли б знайти на графіку P-T.

потрібен альт тег — Малюнок\(3.1.1\) (повторюється): Крива тиску пари

Це ще не все. Є й інші наслідки. Чи можемо ми зараз сказати, що критична точка - це максимальне значення тиску і температури, де рідина і газ можуть співіснувати? Подивіться ще раз на рисунок 4.1.4. Очевидно, що ні. Критична точка більше не знаходиться на вершині або піку двофазної області; отже, пара і рідина можуть співіснувати в рівновазі при T > T _c і P > P _c. Насправді ми можемо виділити два нових максимуми: умова P _cc - максимальний тиск, а умова T _cc - максимальна температура, при якій L+V буде знаходитися в рівновазі. Привласнюємо цим пунктам особливі назви. Існують cricondenbar і cricondentherm відповідно.

Зрозуміло, що єдине визначення, яке зараз може триматися для критичної точки - як для сумішей, так і для чистих компонентів - це те, що показано нижче.

Критична точка (P _c, T _c):

Температура і тиск, при якому рідина і пара не відрізняються.

Знову ж таки, це визначення застосовується як для сумішей, так і для чисто компонентних систем; воно не робить жодних посилань на максимальні значення в кривій. Ці максимальні значення, як ми вже говорили, мають особливі назви у випадку сумішей. Таким чином, для сумішей ми повинні додатково визначити:

Тепловий конденсатор (Т _куб.см):

Найвища температура в двофазної оболонці.
Для T > T _cc рідина і пара не можуть співіснувати в рівновазі, незалежно від тиску.

Конденсатор (P _cc):

Найвищий тиск в двофазної оболонці.
Для P > P _cc рідина і пара не можуть співіснувати в рівновазі, незалежно від температури.

У випадку з унарною системою, крім кривих точки роси і бульбашок, що лежать один на одному, зрозуміло, що cricondentherm, cricondentherm і критичні умови також представлені однією точкою (тобто самої критичною точкою). Це зрозуміло з усіх трьох попередніх визначень. Таким чином, як ми бачили раніше, визначення критичної точки в унарних системах охоплює всі три визначення, наведені вище.

Тільки для чистих речовин:

Cricondentherm = Критична температура = Критична точка.