3.2: PV Діаграма для чистих систем

Last updated
Save as PDF

Page ID: 29031

Michael Adewumi
Pennsylvania State University via John A. Dutton: e-Education Institute

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

У попередньому обговоренні ми використовували діаграму P-T і не були стурбовані змінами обсягу системи. Якщо ми хочемо стежити за змінами об'єму, ми можемо побудувати діаграми p-v або t-v, в яких ми тримаємо постійну температуру (T) або тиск (P). Розглянемо випадок діаграми p-v (рис.\(\PageIndex{4}\)).

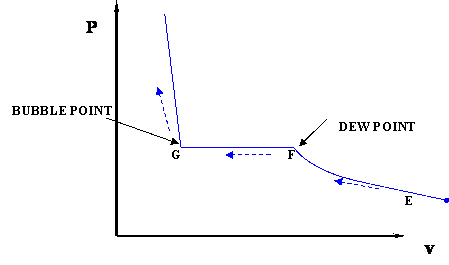
Дивіться текст нижче зображення — Малюнок\(\PageIndex{4}\): Діаграма P-v для чистого компонента

У цьому випадку температура тримається постійною; наша речовина проходить процес ізотермічного стиснення. Починаючи з Е (всепарний стан), підвищення тиску призведе до досить значного зменшення обсягу, оскільки газова фаза стислива. Якщо ми продовжуємо стискати ізотермічно, ми опинимося в точці F, де газ буде насичений і з'явиться перша крапля рідини. Ми дійшли до двофазного стану, де рідина (L) і пара (V) співіснують в рівновазі, вперше, хоча і нескінченно малу кількість рідини.

Як тільки ми досягаємо двофазної умови, те, що відбувається, не є інтуїтивним. Поки ми продовжуємо стискати, зменшуючи обсяг (шлях F-G), тиск системи залишається постійним; ця умова триває до тих пір, поки весь пар не стане рідким. Точка G являє собою останню умову співіснування рідини і пари (L+V), стан насиченої рідини (рідина в рівновазі з нескінченно малою кількістю пари.) Після того, як у нас буде тільки рідина, якщо ми продовжуємо стискати (тобто намагаючись зменшити об'єм рідини), ми будемо спостерігати швидке збільшення тиску, на що вказує крутий нахил на діаграмі p-v. Це пояснюється тим, що рідина практично нестислива, отже, потрібен великий тиск, щоб викликати невелике зменшення обсягу.

Важливо визнати деякі моменти цього процесу. Якщо згадати наші попередні визначення основних понять, то визнаємо точку F, де в інакше повністю газоподібної системі (точка роси системи при заданій температурі) існує лише крихітна кількість рідини. Точно так само точка G є точкою міхура; лише нескінченно маленький міхур пари існує в іншому рідкій системі.

Але почекайте секунду. Спробуємо порівняти малюнок 3.2.4 з малюнком 3.1.2. Чи можемо ми зв'язати їх один з одним? Де шлях F-G на малюнку 3.2.4 представлений на малюнку 3.1.2 (повторюється нижче)?

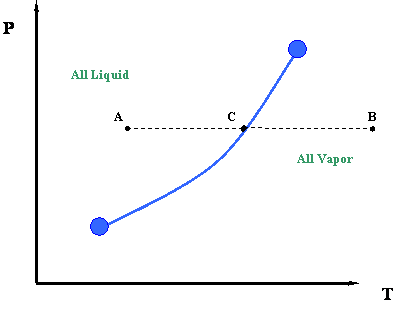
Відповідь полягає в тому, що шлях F-G представлений однією точкою на малюнку 3.1.2; тобто точка С. Нагадаємо, для однокомпонентної системи точки роси і точки бульбашок ідентичні. Під час фазового переходу як тиск, так і температура повинні залишатися постійними для чистих компонентів.

Тепер, якщо ми хочемо створити всі можливі точки, що складають криву тиску пари на малюнку 3.1.2, нам потрібно буде повторити експеримент для різних температур. У підсумку ми отримаємо сімейство ізотерм (кожна подібна до тієї, що представлена на малюнку 3.2.4). Це представлено на малюнку 3.2.5.

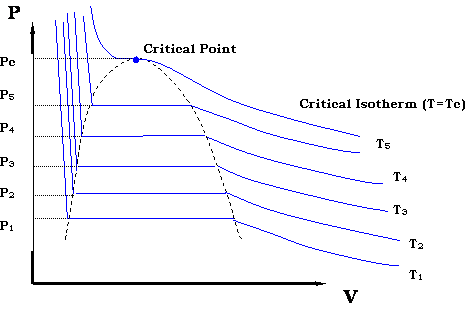
Зона, де ізотерми стають плоскими, окреслює двофазну область. Наочно видно, що шляхом побудови всіх пар в цій зоні (P ₁, T ₁), (P ₂, T ₂)... (P _c, T _c) ми зможемо відтворити малюнок 3.1.2.

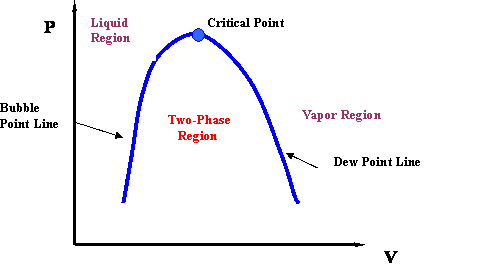
Якщо ми зараз проведемо лінію через всі точки міхура на малюнку 3.2.5, а потім намалюємо лінію, що з'єднує всі точки роси, ми закінчимо кривою точки міхура та кривою точки роси відповідно. Зрозуміло, що дві криві зустрічаються в критичній точці (P _c, T _c). Крім того, дві криві окреслюють фазову оболонку, яка містить 2-фазну область всередині. Якщо ми трохи «зачистимо» рис. 3.2.5, то закінчуємо фазовою оболонкою, яка показана на рис. 3.2.6.

Якщо уважно стежити за тенденцією критичної ізотерми (@ T = T _c на рис. 3.2.5), то зрозумієте, що вона має точку перегину (зміни кривизни) в критичній точці. Крім того, критична точка також представляє максимальну точку (вершину) оболонки p-v. Математично ця інформація передається виразами:

\[ \left( \frac{\partial P}{\partial V} \right)_{Pc,Tc} = \left( \frac{\partial^2 P}{\partial V^2} \right)_{Pc,Tc} = 0 \nonumber \]

які зазвичай відомі як умови критичності. Ці умови завжди виконуються в критичній точці. Ми будемо коментувати це більше після того, як ми почнемо обговорення Рівняння стану (EOS) - напівемпіричні відносини, які математично моделюють p-v-t поведінку рідин.