3.1: Статичний контролер зворотного зв'язку

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Система управління зворотним зв'язком

Стандартна блок-схема системи управління зворотним зв'язком з одним входом (SISO) включає установку $G(s)$ , контролер $K(s)$ , і датчик $H(s)$ , де $H\left(s\right)=1$ часто передбачається.

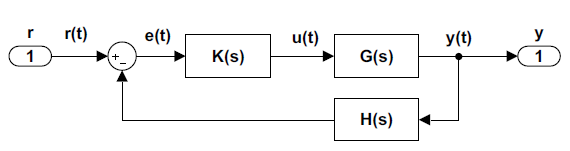
Загальна функція передачі системи від входу $r(t)$ , до виходу $y(t)$ , може бути отримана, враховуючи сигнал помилки, $e=r-Hy=r-KGHe$ . Таким чином, $\left(1+KGH\right)e=r$ .

Нехай $L\left(s\right)=KGH(s)$ позначають посилення зворотного зв'язку петлі; потім, $\left(1+L\right)e=r$ .

Функція передачі помилок від $r$ до $e$ виходить у вигляді:

$S(s)=\frac{1}{1+L(s)}=\frac{1}{1+KGH(s)}$

Функція передачі замкнутого циклу від $r$ до $y$ виходить у вигляді:

$T(s)=\frac{KG(s)}{1+KGH(s)}$

Відзначимо, що: $S\left(s\right)+T\left(s\right)=1$ .

Статична конструкція контролера петлі

Статичний контролер позначає використання підсилювача з коефіцієнтом посилення, $K$ , для генерації входу на установку, $G(s)$ . Дія контролера представлена у вигляді: $u=Ke$ , де $e$ представляє сигнал помилки і $u$ є введенням рослини.

Малюнок $\PageIndex{2}$ : Система управління зворотним зв'язком зі статичним регулятором посилення.

Припускаючи $H(s)=1$ , що функція передачі із замкнутим циклом задається як:

$\frac{y\left(s\right)}{r\left(s\right)}=T\left(s\right)=\frac{KG(s)}{1+KG\left(s\right)}$

Нехай $G\left(s\right)=\frac{n\left(s\right)}{d\left(s\right)}$ ; потім, функція передачі замкнутого циклу виходить у вигляді:

$\frac{y\left(s\right)}{r\left(s\right)}=\frac{Kn\left(s\right)}{d\left(s\right)+Kn(s)}$

Характеристичний многочлен із замкнутим контуром визначається як: $\mathit{\Delta}\left(s,K\right)=d(s)+Kn\left(s\right)$ .

З точки зору проектування контролера коефіцієнт посилення $K$ може бути обраний для досягнення бажаних місць розташування коренів для характеристичного полінома із замкнутим контуром. Конструкція може бути виконана шляхом порівняння коефіцієнтів характеристичного многочлена з потрібним характеристичним поліномом.

Приклад $\PageIndex{1}$

Модель для системи екологічного контролю наведено у вигляді: $G\left(s\right)=\frac{1}{20s+1}$ .

Припускаючи статичний регулятор посилення, характеристичний поліном із замкнутим контуром виходить як: $\mathit{\Delta}\left(s,K\right)=20s+1+K$ .

Припустимо, потрібний характеристичний многочлен вибирається як: ${\mathit{\Delta}}_{des}\left(s\right)=4(5s+1)$ . Потім, порівнявши коефіцієнти, отримаємо статичний контролер як: $K=3$ .

Приклад $\PageIndex{2}$

Модель системи управління позицією наведено у вигляді: $G\left(s\right)=\frac{1}{s\left(0.1s+1\right)}$ .

Припускаючи статичний регулятор посилення, характеристичний многочлен виходить у вигляді: $\mathit{\Delta}\left(s,K\right)=s(0.1s+1)+K$ .

Припустимо, потрібний характеристичний многочлен вибирається як: ${\mathit{\Delta}}_{des}\left(s\right)=0.1(s^2+10s+50)$ . Потім, порівнявши коефіцієнти, отримаємо статичний контролер як: $K=5$ .