2.1: Ферми

Вступ

Ферма - це збірка довгих струнких конструктивних елементів, які з'єднуються на їх кінцях. Ферми знаходять значне застосування в сучасному будівництві, наприклад, як вежі (див. Рис. 1), мости, риштування тощо Окрім практичного значення як корисних конструкцій, елементи ферм мають розмірну простоту, що допоможе нам далі розширити концепції механіки, введені в модулі справа з одновісним відгуком. Цей модуль також використовуватиме ферми для введення важливих понять у статиці та числовому аналізі, які будуть розширені в наступних модулів до більш загальних проблем.

Малюнок\(\PageIndex{1}\): Фермові вежі, що підтримують вітрову турбіну NASA/GE MOD-1 в Буні, Північна Кароліна (ліворуч) та дослідницьку вітрову турбіну NASA MOD-0 в Сандаскі, штат Огайо (праворуч). (Громадське надбання; через Вікіпедію)

Приклад\(\PageIndex{1}\)

Ферми часто використовуються для посилення конструкцій, і більшість людей знайомі з часто дуже складними системами поперечних кріплень, що використовуються в мостах. Кроквяні кріплення, що використовуються для жорсткості веж підвісних мостів проти вигин, важко пропустити, але не всі помічають вертикальні фермові панелі на більшості таких мостів, які служать для посилення жорсткості палуби від деформації згинання та кручення.

Багато читачів побачать дуже відомий фільм, знятий 7 листопада 1940 року Барні Елліоттом з магазину камер у Такомі, штат Вашингтон. Вітер поривав до 42 миль/год того дня, і викликав послідовність вражаючих хвиль і можливого краху мосту Такома звужується (Інтерактивний навчальний відеодиск колапсу Такома Вузький міст доступний з Wiley Educational Software (ISBN 0-471-87320-9).). Цей міст був побудований з використанням відносно коротких двотаврових балок для жорсткості палуби, а не кроквяних панелей, як повідомляється, з естетичних міркувань; мостові конструкції періоду сприяли все більш струнким і витонченим конструкціям. Ще при будівництві міст став добре відомий своєю тривожною тенденцією погойдуватися на вітрі, заробивши йому місцеве прізвисько «Галопуюча Герті».

Ребра жорсткості ферми використовувалися, коли міст був перебудований в 1950 році, і новий міст був вільний від коливань, які призвели до обвалення його попередника. Це хороший приклад одного важливого використання ферм, але це, мабуть, ще кращий приклад цінності обережності та смирення в інженерії. Відповіді на гліб, які часто даються для початкового колапсу - резонансні пориви вітру, вихори фон Кармана тощо - насправді не є задовільними за межами очевидного твердження про те, що колода була недостатньо жорсткою. Навіть сьогодні знаючі інженери сперечаються про дуже складну структурну динаміку. Зрештою, багато невизначеностей існує навіть у дизайні, виконаних із застосуванням дуже сучасних та складних методів. Мудрий дизайнер ніколи не буде повністю довіряти теоретичному результату, створеному комп'ютером чи ні, і максимально скористається досвідом і інтуїцією.

Статичний аналіз сил

Ньютон зауважив, що маса прискорюється відповідно до векторної суми прикладених до неї сил:\(\sum F = ma\). (Векторні величини, позначені жирним шрифтом.) У структурах, які закріплені так, щоб запобігти руху, очевидно, немає прискорення, і сили повинні дорівнювати нулю. Це векторне рівняння має стільки скалярних складових, скільки розмірність задачі; для двовимірних випадків ми маємо:

\[\sum F_x = 0\]

\[\sum F_y = 0\]

де\(F_x\) і\(F_y\) є складовими\(F\) в\(x\) і\(y\) декартових координатних напрямках. Ці два рівняння, які ми можемо інтерпретувати як стримуючі структуру від поступального руху в\(y\) напрямках\(x\) і, дозволяють вирішити не більше двох невідомих сил у структурних задачах. Якщо структура обмежена обертанням, а також перекладом, ми можемо додати рівняння моменту, яке стверджує, що сума моментів або крутних моментів у\(x-y\) площині також повинна додаватися до нуля:

\[\sum M_{xy} = 0\]

Тоді у двох вимірах ми маємо три рівняння статичної рівноваги, які можуть бути використані для вирішення невідомих сил. У трьох вимірах додається третє рівняння сили та ще два рівняння моменту, загалом шість:

\[\begin{array} {c} {\sum F_x = 0 \ \ \ \ \ \ \sum M_{xy} = 0} \\ {\sum F_y = 0 \ \ \ \ \ \ \sum M_{xz} = 0} \\ {\sum F_z = 0 \ \ \ \ \ \ \sum M_{yz} = 0} \end{array}\]

Ці рівняння можуть бути застосовані до структури в цілому, або ми можемо (концептуально) видалити шматок конструкції і розглянути сили, що діють на видалений шматок. Ескіз твору, що показує всі сили, що діють на нього, називається діаграмою вільного тіла. Якщо кількість невідомих сил на діаграмі дорівнює або менше кількості наявних рівнянь статичної рівноваги, невідомі можуть бути вирішені простим способом; такі задачі називаються статично детермінантними. Зверніть увагу, що ці рівняння рівноваги нічого не припускають про матеріал, з якого виготовлена структура, тому отримані сили також не залежать від матеріалу.

В аналізах, які будуть розглянуті тут, передбачається, що елементи ферми з'єднуються між собою штифтами або іншими такими з'єднаннями, які дозволяють вільне обертання навколо стику. Як видно на діаграмі вільного тіла на малюнку 2, ця нездатність чинити опір обертанню означає, що сила, що діє на штифтовий шарнір фермового елемента, повинна бути в осьовому напрямку елемента: будь-яка поперечна складова, як правило, спричиняє обертання, і якщо елемент повинен бути в статичній рівновазі сили рівняння моменту поперечна складова зникає. Якщо кінці елементів повинні були бути зварені або болтові, а не просто заколоти, кінцеве з'єднання могло б передавати поперечні зусилля і згинальні моменти в елемент. Така конструкція тоді називалася б рамою, а не фермою, і її аналіз повинен був би включати ефекти згинання. Такі конструкції будуть оброблятися в Модулі на вигин.

Малюнок 2: Закріплені елементи не можуть витримувати поперечні навантаження.

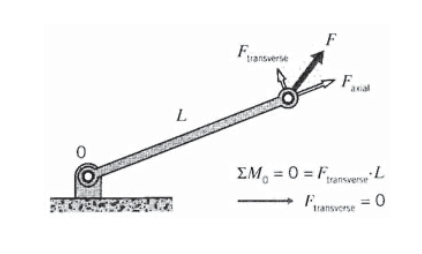
Знання того, що сила в кожному кроквяному елементі повинна бути в осьовому напрямку елемента, є ключем до вирішення для елементів сил в фермах, що містять багато елементів. Кожен елемент, що зустрічається на штифтовому з'єднанні, буде тягнути або натискати на штифт залежно від того, чи знаходиться елемент в напрузі або стисненні, і оскільки штифт повинен знаходитися в статичній рівновазі, сума всіх сил елемента, що діють на штифт, повинна дорівнювати силі, яка зовні прикладається до штифта:

\[\sum_{e} F_i^e = F_i \nonumber\]

Тут верхній\(e\) індекс вказує на векторну силу, що подається елементом на\(i^{th}\) штирі в фермі та\(F_i\) в силі, що зовнішньо прикладається до цього штифта. Підсумовування відбувається по всіх елементах, з'єднаних зі штирем.

Приклад\(\PageIndex{2}\)

Дуже проста двоелементна ферма, часто зустрічається в шкільних підручниках фізики і показана на малюнку 3, може бути проаналізована таким чином. Інтуїція говорить нам, що верхній елемент, з'єднуючи суглоби\(A\) і\(B\), знаходиться в напрузі, а елемент\(BC\) знаходиться в стисненні. У більш складних завданнях не завжди можна визначити ознаку сили елемента шляхом огляду, але це не має значення. При накресленні діаграм вільного тіла для штирів навантаження можна провести в будь-якому напрямку; якщо припущення виявиться неправильним, рішення дасть негативне значення величини сили.

Невідомі сили на сполучному\(B\) штирі знаходяться в напрямку прикріплених до нього елементів, і оскільки таких сил всього дві, вони можуть бути визначені з двох рівнянь сили статичної рівноваги:

Малюнок 3: Двоелементна ферма.

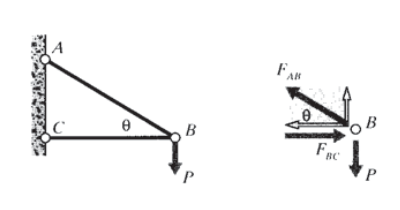
\[\sum F_y = 0 = + F_{AB} \sin \theta - P \Rightarrow F_{AB} = \dfrac{P}{\sin \theta}\nonumber\]

\[\sum F_x = 0 = -F_{AB} \cos \theta + F_{BC} \Rightarrow F_{BC} = F_{AB} \cos \theta = \dfrac{P}{\tan \theta}\nonumber\]

У більш складних фермах загальний підхід полягає в тому, щоб почати з штифтового з'єднання, що містить не більше двох елементів, що мають невідомі сили, а потім працювати від стику до з'єднання, використовуючи зусилля елемента з попереднього кроку, щоб зменшити кількість невідомих. Розглянемо 6-елементну ферму, показану на малюнку 4, в якій стики і елементи пронумеровані так, як зазначено, при цьому номери елементів фігурують колами. Суглоб 3 є природною відправною точкою, так як тільки сили\(F_2\) і\(F_5\) здаються невідомими. Як тільки F5 знайдений, аналіз суглоба 5 має тільки сили\(F_4\) і\(F_6\) як невідомо. Нарешті, діаграма вільного тіла вузла 2 може бути завершена, оскільки тільки\(F_1\) і\(F_3\) зараз невідомі. Потім аналіз сили завершується.

Малюнок 4: Шестиелементна ферма.

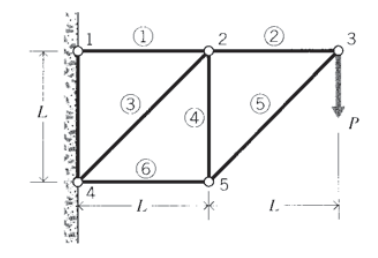
Часто існує багато способів вирішити такі проблеми, як це, можливо, з деякими легше, ніж інші. Інший підхід може полягати в тому, щоб почати з одного зі стиків біля стіни; тобто стик 1 або стик 4. Проблема, як спочатку зазначено, дає ці суглоби як мають фіксовані зсуви, а не задані сили. Це приклад змішаної крайової задачі, при якій деякі частини кордону мають задані сили, а інші частини мають задані зсуви. Такі задачі, як правило, складніші і вимагають більше математичної інформації для їх вирішення, ніж задачі, що мають тільки той чи інший тип граничної умови. Однак у статично визначених задачах конструкція може бути перетворена в тип тільки навантаження шляхом виклику статичної рівноваги на конструкції в цілому. Потім граничні умови з фіксованим зміщенням замінюються силами реакції, які встановлюються в точках обмеження.

Малюнок 5: Діаграма вільного тіла шестиелементної ферми

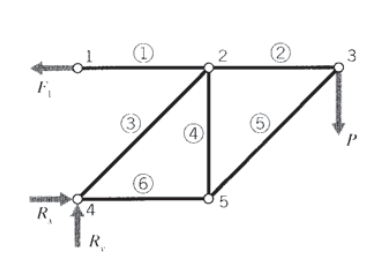
Рівняння моментної рівноваги не були корисними при спільному аналізі, описаному раніше, оскільки окремі елементи не можуть підтримувати моменти. Але як видно на малюнку 5, ми можемо розглянути 6-елементну ферму в цілому і приймати моменти навколо стику 4. Оскільки моменти проти годинникової стрілки є позитивними, це дає

\[\sum M_4 = 0 = F_1 \times L - P \times 2 L \Rightarrow F_1 = 2P\nonumber\]

Сила\(F_1\) - це сила, прикладена стіною до стику 1, і це, очевидно, дорівнює силі розтягування в елементі 1. Вертикальної складової цієї сили реакції бути не може, так як сили елемента повинні бути осьовими і тільки елемент 1 підключений до стику 1. При стику 4 сили реакції Rx і Ry можуть діяти в обох\(y\) напрямках\(x\) і, так як елемент 3 не перпендикулярний стіні. Ці сили реакції можна знайти, викликаючи горизонтальну і вертикальну рівновагу:

\[\sum F_x = 0 = -F_1 + R_x \Rightarrow R_x = F_1 = 2P\nonumber\]

\[\sum F_y = 0 = + R_y - P \Rightarrow R_y = P\nonumber\]

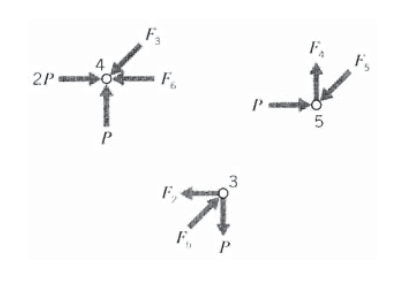
Спільний аналіз тепер можна починати з суглоба 4, оскільки там діють лише дві невідомі сили (див. Рис. Для вертикальної рівноваги\(F_3 \cos 45 = P\), так\(F_3 = \sqrt{2} P\). Тоді для горизонтальної рівноваги\(F_6 + F_3 \cos 45 = 2P\), так\(F_6 = P\). Тепер рухаючись до суглоба 5, горизонтальна рівновага дає\(F_5 \cos 45 = P\) так\(F_5 = F_3 = \sqrt{2} P\), і вертикальна рівновага дає\(F_4 = F_5 \cos 45\) так\(F_4 = P\). Нарешті, при суглобі 3 горизонтальна рівновага дає\(F_2 = F_5 \cos 45\) так\(F_2 = P\).

Малюнок 6: Індивідуальні схеми стиків.

У фактичній конструкції ферми, як тільки сила кожного елемента відома, його площа поперечного перерізу може бути розрахована таким чином, щоб зберегти напругу елемента відповідно до\(\sigma = P/A\) безпечного менше, ніж межа текучості матеріалу. Елементи стиснення, однак, також повинні бути проаналізовані на вигин, оскільки їх співвідношення\(EI\) до\(L^2\), як правило, низькі. Навантаження на вигин може бути значно збільшено, закріпивши елемент проти бокового відхилення, і це кріплення очевидно в більшості мостів і кранів. Також кроквяні елементи зазвичай скріплюються зварними або болтовими з'єднаннями, а не штирями. Ці з'єднання можуть нести деякі згинальні моменти, що допомагає жорсткості ферми проти вигин.

прогини

У деяких додатках може бути важливо, щоб ферма була досить жорсткою, щоб зберегти деформації всередині заданих меж. Астрономічні телескопи є прикладом, оскільки відхилення конструкції, що підтримує оптичні вузли, може погіршити фокусуючу здатність приладу. Типова вишка або міст, однак, ймовірно, швидше за все, буде міцністю, а не критичною жорсткістю, тому може здатися, що прогини будуть відносно неважливими. Однак буде видно, що розгляд прогинів необхідний для вирішення великої кількості конструкцій, які не є статично визначеними. Наступні розділи обробляють прогини ферм з обох цих причин.

Геометричний підхід

Після того, як відома осьова сила в кожному кроквяному елементі, деформації окремих елементів слідують безпосередньо за допомогою\(\delta = PL/AE\). Прогин будь-якої точки в фермі потім можна визначити геометрично, посилаючись на вимогу, щоб елементи залишалися закріпленими між собою в місцях їх кріплення. У симетричній двоелементної фермі, показаної на малюнку 7, стик\(B\) буде явно відхилятися вниз по вертикалі. Співвідношення між\(\delta\) осьовою деформацією елементів і вертикальним прогином суглоба\(\delta_v\) потім розглядається як

\[\delta_v = \dfrac{\delta}{\cos \theta}\nonumber\]

Тут передбачається, що деформація досить мала, щоб грубі аспекти геометрії були по суті незмінними; в цьому випадку кут\(\theta\) однаковий до і після прикладання навантаження.

Малюнок 7: Двоелементна ферма.

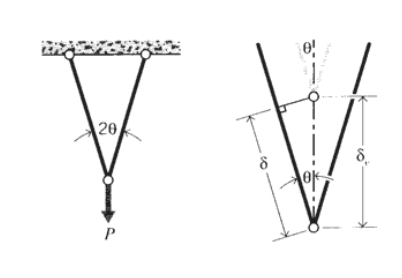
У геометричному аналізі більш складних ферм іноді зручно візуалізувати розкріплення елементів на вибраному стику, дозволяючи елементам подовжуватися або стискатися відповідно до осьової сили, яку вони передають, а потім розгойдуючи їх навколо нерухомого штифтового з'єднання, поки місця штифтів не збігаються знову. Рух незакріплених кінців буде простежувати кругові шляхи, але якщо прогини невеликі, шлях можна наблизити як пряму лінію, перпендикулярну осі елемента. Потім спільну позицію можна обчислити з піфагорієвських відносин.

У більш ранній двоелементної фермі, показаної на малюнку 3, ми мали\(P_{AB} = P/ \sin \theta\) і\(P_{BC} = P/ \tan \theta\). Якби штир на стику\(B\) були зняті, прогини елемента були б

\[\delta_{AB} = \dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \text{ (tension)}\nonumber\]

\[\delta_{BC} = \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{BC} \text{ (compression)}\nonumber\]

Тоді загальний прогин\(B\) суглоба вниз

\[\delta_v = \delta_1 + \delta_2= \dfrac{\delta_{AB}}{\sin \theta} + \dfrac{\delta_{BC}}{\tan \theta}\nonumber\]

\[= \dfrac{P}{\sin^2 \theta} \left ( \dfrac{L}{AE} \right )_{AB} + \dfrac{P}{\tan^2 \theta} \left ( \dfrac{L}{AE} \right )_{BC} \nonumber\]

Ці прогини показані на малюнку 8.

Малюнок 8: Зсуви в двоелементної фермі.

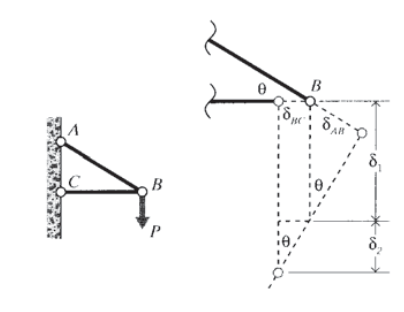
Горизонтальний прогин\(\delta_h\) штифта обчислити простіше, так як це всього лише стиснення елемента\(BC\):

\[\delta_h = \delta_{BC} = \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{BC} \nonumber\]

Енергетичний підхід

Геометричний підхід до аналізу деформації ферми може бути досить стомлюючим, тим більше, що проблеми стають більшими. Багато проблем можна вирішити легше, використовуючи енергію деформації, а не підхід «сила в точці». Загальна енергія деформації\(U\) в одному пружно навантаженому кроквяному елементі становить

\[U = \int P\ d\delta\nonumber\]

Приріст деформації\(d\delta\) пов'язаний з відповідним збільшенням навантаження\(dP\) на

\[\delta = \dfrac{PL}{AE} \Rightarrow d\delta = \dfrac{L}{AE} dP\nonumber\]

Тоді енергія деформації

\[U = \int P \dfrac{L}{AE} dP = \dfrac{P^2L}{2AE}\nonumber\]

Малюнок 9: Збільшення енергії деформації та компліментарної деформації.

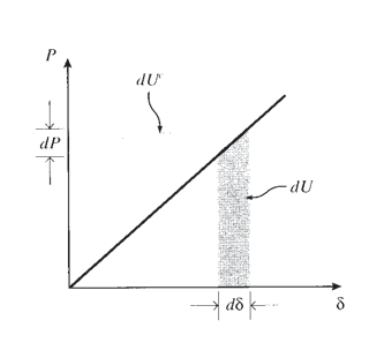
Інкрементне збільшення енергії деформації, що відповідає збільшенню деформації,\(d\delta\) є справедливим\(dU = P d\delta\). Якщо крива силового подовження лінійна, це ідентично збільшенню величини, яка називається додатковою енергією деформації:\(dU^c = \delta dP\). Ці величини зображені на малюнку 9. Тепер розглянемо систему з безліччю з'єднань, що піддаються ряду навантажень, що діють на різних стиках. Якби ми трохи збільшували\(i^{th}\) навантаження, утримуючи всі інші навантаження постійними, збільшення загальної додаткової енергії системи було б

\[dU^c = \delta_i dP_i\nonumber\]

де\(\delta_i\) - зміщення, яке відбувалося б в місці розташування\(P_i\), рухаючись в тому ж напрямку, що і вектор сили для\(P_i\). Перестановка,

\[\delta_i = \dfrac{\partial U^c}{\partial P_i}\nonumber\]

і так як\(U^c = U\):

\[\delta_i = \dfrac{\partial U}{\partial P_i}\]

Отже, зміщення в заданій точці є похідною загальної енергії деформації по відношенню до навантаження, що діє в цій точці. Це забезпечує основу надзвичайно корисного методу аналізу переміщень, відомого як теорема Кастільяно (З тези 1873 року італійського інженера Альберто Кастільяно (1847—1884), в Туринському політехнічному інституті.), який можна констатувати для проблем ферми наступним рецептом:

1. Нехай навантаження, прикладене на суглоб, деформація якого шукається, у напрямку бажаної деформації, записується як алгебраїчна змінна, скажімо\(Q\). Якщо навантаження відома чисельно, замініть число на букву. Якщо в потрібному місці і напрямку навантаження немає, поставте туди уявну, яка буде встановлена на нуль в кінці завдання.
2. Вирішіть для зусиль\(F_i(Q)\) в кожному кроквяному елементі, кожен з яких може залежати від навантаження,\(Q\) призначеної на попередньому етапі.
3. Використовуйте ці сили для обчислення енергії деформації для кожного елемента та підсумуйте енергії в кожному елементі, щоб отримати загальну енергію деформації для ферми:
   \[U_{tot} = \sum_{i} U_i = \sum_i \dfrac{F_i^2 L_i}{2A_i E_i}\]
   Кожен член цього підсумовування може містити змінну\(Q\).
4. Деформація конгруентна до\(Q\), тобто деформація в точці, де\(Q\) застосовується і в тому ж напрямку\(Q\), що і, потім
   \[\delta_Q = \dfrac{\partial U_{tot}}{\partial Q} = \sum_i \dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i (Q)}{\partial Q}\]
5. Навантаження\(Q\) замінюється її числовим значенням, якщо відомо. Або на нуль, якщо це була уявна навантаження в першу чергу.

Застосовуючи цей метод до вертикального прогину двоелементної ферми малюнка 3, завдання вже має силу в необхідному напрямку, прикладену вниз навантаження\(P\). Сили вже були показані\(P_{AB} = P/ \sin \theta\) і\(P_{BC} = P/ \tan \theta\), тому вертикальний прогин можна записати відразу як

\[\begin{align*} \delta_v &= P_{AB} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{\partial P_{AB}}{\partial P} + P_{BC} \left ( \dfrac{L}{AE} \right )_{BC} \dfrac{\partial P_{BC}}{\partial P} \\[4pt] &=\dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{1}{\sin \theta} + \dfrac{P}{\tan \theta} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{1}{\sin \theta} + \dfrac{P}{\tan \theta} \left ( \dfrac{AE}{L} \right )_{BC} \dfrac{1}{\tan \theta} \end{align*}\]

Це ідентично виразу, отриманому з геометричних міркувань. Енергетичний метод не врятував занадто багато алгебраїчних кроків у цьому випадку, але уникав необхідності візуалізувати та ідеалізувати переміщення геометрично.

Якщо потрібне горизонтальне зміщення на\(B\) стику, метод вимагає, щоб в цій точці існувала горизонтальна сила. Одного не дано, тому ми розміщуємо там уявний, скажімо\(Q\). Потім ферма повторно аналізується статично, щоб знайти, як сили елемента впливають на цю нову силу\(Q\). Сила верхнього елемента така,\(P_{AB} = P/\sin \theta\) як і раніше, а сила нижнього елемента стає\(P_{BC} = P/ \tan \theta - Q\). Повторюючи процес Кастільяно, але тепер диференціюючи щодо\(Q\)

\[\delta_h = P_{AB} \left ( \dfrac{L}{AE} \right )_{AB} \dfrac{\partial P_{AB}}{\partial P} + P_{BC} \left ( \dfrac{L}{AE} \right )_{BC} \dfrac{\partial P_{BC}}{\partial P}\nonumber\]

\[= \dfrac{P}{\sin \theta} \left ( \dfrac{L}{AE} \right )_{AB} \cdot 0 + \left (\dfrac{P}{\tan \theta} - Q \right ) \left ( \dfrac{L}{AE} \right )_{BC} (-1)\nonumber\]

Перший термін зникає при диференціації, оскільки\(Q\) не з'явився у виразі for\(P_{AB}\). Це спосіб помітити, що горизонтальний прогин визначається повністю стисненням елемента\(BC\). Після встановлення\(Q = O\) кінцевий результат

\[\delta_h = -\dfrac{P}{\tan \theta} \left ( \dfrac{AE}{L} \right )_{BC}\nonumber\]

як і раніше.

Приклад\(\PageIndex{3}\)

Розглянемо 6-елементну ферму малюнка 4, сили окремих елементів якої були знайдені раніше діаграмами вільного тіла. Шукаємо вертикальний прогин вузла 3, який конгруентний силі\(P\). Використовуючи метод Кастільяно, цей прогин є похідною загальної енергії деформації по відношенню до\(P\). Аналогічно, ми можемо диференціювати енергію деформації кожного елемента по відношенню до\(P\) окремо, а потім додати внески кожного елемента для отримання кінцевого результату:

\[\delta_P = \dfrac{\partial}{\partial P} \sum_i \dfrac{F_i^2L_i}{2A_i E_i} = \sum_i \left (\dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i}{\partial P} \right )\nonumber\]

Для систематизації такого підходу ми можемо сформувати таблицю необхідних параметрів наступним чином:

\(i\)	\(F_i\)	\(\dfrac{L_i}{A_iE_i}\)	\(\dfrac{\partial F_i}{\partial P\)	\(\dfrac{F_i L_i}{A_i E_i} \dfrac{\partial F_i}{\partial P}\)
1	\(2P\)	\(L/AE\)	2	\(4PL/AE\)
2	\(P\)	\(L/AE\)	1	\(PL/AE\)
3	\(\sqrt{2} P\)	\(\sqrt{2} L/AE\)	\(\sqrt{2}\)	\(2.83 PL/AE\)
4	\(P\)	\(L/AE\)	1	\(PL/AE\)
5	\(\sqrt{2} P\)	\(\sqrt{2} L/AE\)	\(\sqrt{2}\)	\(2.83 PL/AE\)
6	\(P\)	\(L/AE\)	1	\(PL/AE\)

Якщо, наприклад, у нас є числові параметри\(P = 1000\ lbs\)\(L = 100\ in\),\(E = 30\ Mpsi\) і\(A = 0.5\ in^2\), потім\(\delta_P = 0.0844\ in\).

Статично невизначені ферми

Вже було відзначено, що сили елемента в проблемах ферми, розглянутих до цього часу, не залежать від властивостей матеріалів, що використовуються в їх конструкції, так само, як напруга в простому випробуванні на розтяг не залежить від матеріалу. Цей результат, який, безумовно, полегшує вирішення проблеми, є наслідком того, що попередні задачі є статично визначеними; тобто можуть бути розв'язані лише за допомогою рівнянь статичної рівноваги. Статична детермінантність, отже, є важливим аспектом складності, яку ми можемо очікувати при вирішенні проблеми. Не всі проблеми статично визначаються, і одним з наслідків цієї невизначеності є те, що сили в конструкції можуть залежати від властивостей матеріалу.

Провівши статичний аналіз ферми в цілому для знаходження сил реакції на опорах, ми зазвичай намагаємося знайти зусилля елемента, використовуючи описаний вище метод «шарнір за часом». Однак у двовимірній задачі ферми може бути щонайбільше дві невідомі сили на штифтовому з'єднанні, якщо стик повинен бути вирішений лише за допомогою статики, оскільки рівняння моменту не дає корисної інформації в цьому випадку. Якщо більше невідомих присутній незалежно від того, в якому порядку аналізуються кроквяні з'єднання, то необхідно знайти ряд додаткових рівнянь, рівних іншим невідомим. Ці додаткові рівняння - це ті, що забезпечують сумісність різних зміщень суглобів, кожен з яких повинен бути таким, щоб тримати фермові з'єднання закріпленими разом.

Приклад\(\PageIndex{4}\)

Простий приклад, всього два кроквяних елементи, що діють паралельно, як показано на малюнку 10, покаже необхідний підхід. Тут умова сумісності просто

\[\delta_A = \delta_B\nonumber\]

Малюнок 10: Два кроквяних елемента паралельно.

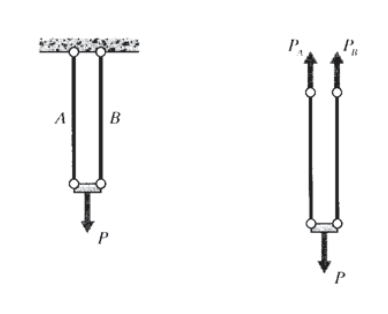
Зміщення окремих елементів пов'язані з силами елемента\(\delta = PL/AE\), який є матеріально залежним і може бути названий складовим рівнянням, оскільки воно відображає механічну конституцію матеріалу. Поєднання цього з умовою сумісності дає

\[\dfrac{P_AL}{A_A E_A} = \dfrac{P_BL}{A_BE_B} \Rightarrow P_B = P_A \dfrac{A_BE_B}{A_AE_A}\nonumber\]

Нарешті, окремі сили елемента повинні складати до загальної прикладеної навантаження,\(P\) щоб задовольнити рівновагу:

\[P = P_A + P_B = P_A + P_A \dfrac{A_BE_B}{A_A E_A} \Rightarrow P_A = P \left (\dfrac{1}{1 + (\tfrac{A_BE_B}{A_AE_A})} \right )\nonumber\]

Зверніть увагу, що остаточна відповідь в наведеному вище прикладі залежить від розмірів елемента і жорсткості матеріалу, як і обіцяно. Тут умова геометричної сумісності була дуже простою і очевидною, а саме те, що зміщення торцевих з'єднань двох елементів були однаковими. У більш складних фермах ці відносини можуть бути тонкими, але, як правило, стають більш очевидними з практикою.

У вищезгаданій задачі були використані три різні типи відносин: рівняння сумісності, яке вказує, як структура повинна деформуватися кінематично, щоб залишатися пов'язаною; складове рівняння, що втілює реакцію матеріалу напруження-деформація; і рівняння рівноваги, в якому зазначено, що сили повинні сума до нуля, якщо слід уникати прискорення. Ці три концепції, зроблені дещо більш загальним математично для вирішення геометрично більш складних проблем, лежать в основі всієї твердої механіки.

У модулі про пружний відгук ми зазначили, що напруження в розтяжному зразку визначається лише міркуваннями статичної рівноваги, що задається\(\sigma = P/A\) незалежними від властивостей матеріалу. Тепер ми бачимо, що статична детермінантність залежить, серед іншого, від того, який матеріал є однорідним, тобто однаковим у всьому. Якщо зразок на розтяг складається з двох субодиниць, кожна з яких має різні властивості, напруги будуть розподілятися по-різному між двома одиницями, і напруги не будуть рівномірними. Всякий раз, коли формула напруження або деформації копіюється з довідника, користувач повинен бути обережним, щоб відзначити обмеження основної теорії. Формули довідника, як правило, застосовні лише до однорідних матеріалів у їх лінійному пружному діапазоні, і теорії вищого порядку повинні використовуватися, коли ці умови не виконуються.

Приклад\(\PageIndex{5}\)

Малюнок 11: (а) Триелементна статично невизначена ферма. (b) Діаграма вільного тіла вузла 4. (c) Прогини в вузлі 4.

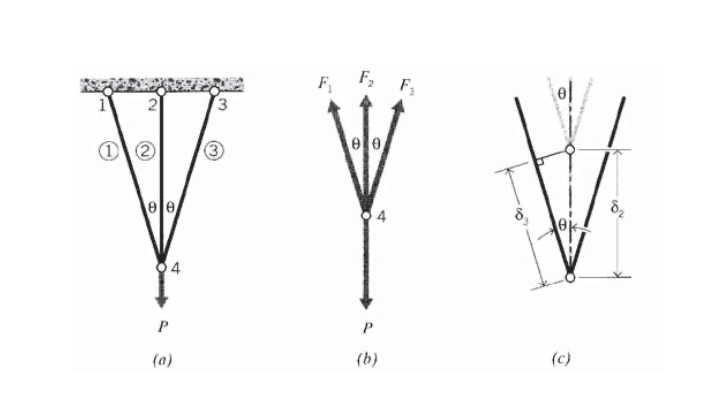
На малюнку 11 (а) показана інша статично невизначена ферма, причому три елементи мають однакову площу і модуль 11, але різної довжини, що зустрічаються в загальному вузлі. З першого погляду ми бачимо, що вузол 4 має три елементи, що зустрічаються там, сили яких невідомі, і це ще одне більше, ніж корисні рівняння статичної рівноваги зможуть впоратися. Це видно і на діаграмі вільного тіла на малюнку 11 (б): горизонтальна і вертикальна рівновага дає

\[\sum F_x = 0 = -F_1 + F_2 \to F_1 = F_2\nonumber\]

\[\sum F_y = 0 = -P + F_2 + F_1 \cos \theta + F_3 \cos \theta \to F_2 + 2 F_3 \cos \theta = P\]

Цих двох рівнянь явно недостатньо для визначення невідомих\(F_1, F_2, F_3\). Нам потрібно інше рівняння, і це забезпечується, вимагаючи деформації бути такою, щоб тримати ферму закріпленою разом у вузлі 4. Оскільки симетрія завдань говорить нам про те, що прогин там прямий вниз, можна використовувати діаграму на малюнку 11 (в). А так як прогин невеликий щодо довжин елементів, кут елемента 3 залишається істотно незмінним після деформації. Це дозволяє нам писати

\[\delta_3 = \delta_2 \cos \theta\nonumber\]

або

\[\dfrac{F_3L_3}{A_3E_3} = \dfrac{F_2L_2}{A_2E_2} \cos \theta \nonumber\]

Використовуючи\(A_2 = A_3\)\(E_2 = E_3\),\(L_3 = L\),, і\(L_2 = L \cos \theta\), це стає

\[F_3 = F_2 \cos^2 \theta\nonumber\]

Вирішуючи це одночасно з рівнянням 2.1.8, отримаємо

\[F_2 = \dfrac{P}{1 + 2 \cos^3 \theta}, F_3 = \dfrac{P \cos^2 \theta}{1 + 2 \cos^3 \theta}\nonumber\]

Зверніть увагу, що модуль\(E\) не відображається в цьому результаті, хоча проблема статично невизначена. Якби елементи мали різну жорсткість, однак скасування не відбулося\(E\) б.

Матричний аналіз ферм

Спільний аналіз вільного тіла ферм є нудним для великих і складних конструкцій, особливо якщо статична невизначеність вимагає, щоб сумісність зміщення розглядалася поряд зі статичною рівновагою. Однак навіть статично невизначені ферми можуть бути вирішені швидко і надійно як для сил, так і для переміщень за допомогою прямої числової процедури, відомої як матричний структурний аналіз. Цей метод є попередником більш загального комп'ютерного методу під назвою скінченно-елементний аналіз (FEA), який за останні два десятиліття домінував більшу частину інженерного аналізу. Тут будуть викладені основи матричного аналізу, насамперед як вступ до більш загального використання ЗЕД в аналізі напружень.

Матричний аналіз ферм працює шляхом розгляду жорсткості кожного кроквяного елемента по одному, а потім за допомогою цих жорсткостей визначити зусилля, які задаються в кроквяних елементах зміщеннями з'єднань, зазвичай званих «вузлами» в кінцевому елементному аналізі. Потім зазначивши, що сума сил, внесених кожним елементом до вузла, повинна дорівнювати силі, яка зовні застосовується до цього вузла, ми можемо зібрати послідовність лінійних алгебраїчних рівнянь, в яких вузлові зміщення є невідомими, а прикладені вузлові сили - відомі величини. Ці рівняння зручно записувати в матричному вигляді, що дає методу свою назву:

\[\begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1n} \\ K_{21} & K_{22} & \cdots & K_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ K_{n1} & K_{n2} & \cdots & K_{nn} \end{bmatrix} \left \{ \begin{matrix} u_1 \\ u_2 \\ \cdots \\ u_n \end{matrix} \right \} = \left \{ \begin{matrix} f_1 \\ f_2 \\ \cdots \\ f_n \end{matrix} \right \}\nonumber\]

Тут\(u_i\) і\(f_j\) вказують відхилення у\(i^{th}\) вузлі і силу на\(j^{th}\) вузлі (це насправді були б векторні величини, з підкомпонентами уздовж кожної координатної осі). Масив\(K_{ij}\) коефіцієнтів називається глобальною матрицею жорсткості, причому\(ij\) компонент фізично впливає\(j^{th}\) зміщення на\(i^{th}\) силу. Матричні рівняння можна скорочувати як

\[K_{ij} u_j = f_i \text{ or } Ku = f\]

використовуючи або індекси, або напівжирний шрифт для позначення векторних та матричних величин.

Або сила, що застосовується зовні, або зміщення відома на початку для кожного вузла, і неможливо вказати одночасно як довільне зміщення, так і силу на даному вузлі. Ці передбачені вузлові сили і зсуви є граничними умовами задачі. Завданням аналізу є визначення сил, які супроводжують нав'язані зсуви, і зміщення у вузлах, де застосовуються відомі зовнішні сили.

Матриця жорсткості для одного кроквяного елемента

В якості першого кроку в розробці набору матричних рівнянь, що описують кроквяні системи, нам потрібна залежність між силами і переміщеннями на кожному кінці окремого кроквяного елемента. Розглянемо такий елемент в\(x-y\) площині, як показано на малюнку 12, прикріплений до вузлів\(j\) пронумерованим\(i\) і нахиленим під кутом\(\theta\) від горизонталі.

З огляду на вектор подовження, який\(\delta\) потрібно вирішити в напрямках уздовж і поперечно елементу, подовження в кроквяному елементі можна записати в терміні відмінностей зміщень його кінцевих точок:

\[\delta = (u_j \cos \theta + v_j \sin \theta) - (u_i \cos \theta + v_i \sin \theta)\nonumber\]

Малюнок 12: Індивідуальний кроквяний елемент.

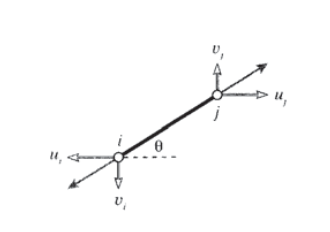
де\(u\) і\(v\) горизонтальна і вертикальна складові прогинів відповідно. (Зсуви у вузлі,\(i\) намальованому на малюнку 12, є негативними.) Це відношення може бути записано в матричному вигляді як:

\[\delta = \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\nonumber\]

Ось\(c = \cos \theta\) і\(s = \sin \theta\).

Малюнок 13: Складові вузлової сили.

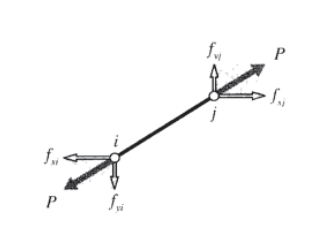
Осьова сила P, яка супроводжує подовження,\(\delta\) задається законом Гука для лінійних пружних тіл як\(P = (AE/L)\delta\). Горизонтальні та вертикальні вузлові сили показані на малюнку 13; їх можна записати через загальну осьову силу як:

\[\left \{ \begin{matrix} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{matrix} \right \} = \left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} P = \left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} \dfrac{AE}{L} \delta\nonumber\]

\[\left \{ \begin{matrix} -c \\ -s \\ c \\ s \end{matrix} \right \} \dfrac{AE}{L} \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\nonumber\]

Проведення множення матриці:

\[\left \{ \begin{matrix} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{matrix} \right \} = \dfrac{AE}{L} \begin{bmatrix} c^2 & cs & -c^2 & -cs \\ cs & s^2 & -cs & -s^2 \\ -c^2 & -cs & c^2 & cs \\ -cs & -s^2 & cs & s^2 \end{bmatrix} \left \{ \begin{matrix} u_i \\ v_i \\ u_j \\ v_j \end{matrix} \right \}\]

Величина в дужках, помножена на\(AE/L\), відома як «матриця жорсткості елемента»\(k_{ij}\). Кожен його термін має фізичне значення, представляючи собою внесок одного з переміщень в одну з сил. Глобальна система рівнянь формується шляхом об'єднання матриць жорсткості елементів з кожного кроквяного елемента по черзі, тому їх обчислення займає центральне місце в методі матричного структурного аналізу. Принципова відмінність методу матричної ферми від загального методу скінченних елементів полягає в тому, як формуються матриці жорсткості елементів; більшість інших комп'ютерних операцій однакові.

Збірка кількох внесків елементів

Малюнок 14: Внесок елемента в загальну вузлову силу.

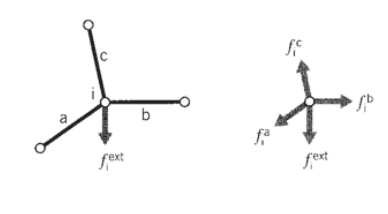
Наступним кроком слід розглянути збірку багатьох кроквяних елементів, з'єднаних штифтовими з'єднаннями. Кожен елемент, що зустрічається на стику, або вузол, сприятиме силі там, як це продиктовано зміщеннями обох вузлів цього елемента (див. Рис. Для підтримки статичної рівноваги всі вклади сили елемента\(f_i^{elem}\) в даному вузлі повинні сумувати силу\(f_i^{ext}\), яка зовнішньо прикладена до цього вузла:

\[f_i^{ext} = \sum_{elem} f_i^{elem} = (\sum_{elelm} k_{ij}^{elem} u_j) = (\sum_{elem} k_{ij}^{elem}) u_j = K_{ij} u_j\nonumber\]

Кожен елемент матриці жорсткості\(k_{ij}^{elem}\) додається до відповідного розташування загальної, або «глобальної» матриці жорсткості\(K_{ij}\), яка пов'язує всі зміщення і зусилля ферми. Цей процес називається «збірка». Індексні номери в зазначеному вище співвідношенні повинні бути «глобальними» номерами, присвоєними кроквяної конструкції в цілому. Однак, як правило, зручно обчислювати окремі матриці жорсткості елементів за локальною схемою, а потім змусити комп'ютер перетворювати в глобальні числа при складанні окремих матриць.

Приклад\(\PageIndex{6}\)

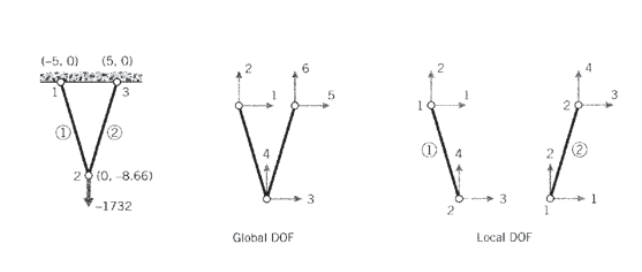
Процес складання лежить в основі методу кінцевих елементів, і варто зробити простий випадок вручну, щоб побачити, як він насправді працює. Розглянемо двоелементну кроквяну задачу на рис. 7, при цьому вузлам присвоюються довільні «глобальні» числа від 1 до 3. Оскільки кожен вузол взагалі може рухатися в двох напрямках, в задачі є 3\(\times\) 2 = 6 загальних ступенів свободи. Глобальна матриця жорсткості буде масивом 6\(\times\) 6, що стосується шести переміщень з шістьма зовнішніми прикладними силами. Тільки одне з переміщень в даному випадку невідомо, так як всі, крім вертикального зміщення вузла 2 (ступінь свободи № 4) обмежені нулем. На малюнку 15 показаний працездатний перелік глобальних чисел, а також «локальних» чисел для кожного окремого елемента.

Використовуючи локальні числа, матрицю жорсткості елементів\(\times\) 4 4 кожного з двох елементів можна оцінити за рівнянням 2.1.10. Кут нахилу розраховується з вузлових координат як

\[\theta = \tan^{-1} \dfrac{y_2 -y_1}{x_2 - x_1}\nonumber\]

Отримана матриця для елемента 1 дорівнює:

Малюнок 15: Глобальна і локальна нумерація для двоелементної ферми.

\[k^{(1)} = \begin{bmatrix} 25.00 & -43.30 & -25.00 & 43.30 \\ -43.30 & 75.00 & 43.30 & -75.00 \\ -25.00 & 43.30 & 25.00 & -43.30 \\ 43.30 & -75.00 & -43.30 & 75.00 \end{bmatrix} \times 10^3\nonumber\]

і для елемента 2:

\[k^{(2)} = \begin{bmatrix} 25.00 & 43.30 & -25.00 & -43.30 \\ 43.30 & 75.00 & -43.30 & -75.00 \\ -25.00 & -43.30 & 25.00 & 43.30 \\ -43.30 & -75.00 & 43.30 & 75.00 \end{bmatrix} \times 10^3\nonumber\]

(Важливо одиниці бути послідовними; тут довжини в дюймах, сили в фунтах, і модулі в фунтах на квадратний дюйм. Модуль обох елементів є\(E = 10\) Mpsi і обидва мають площу\(A = 0.1\ in^2\).) Ці матриці мають рядки і стовпці, пронумеровані від 1 до 4, що відповідають локальним ступеням свободи елемента. Однак кожна з місцевих ступенів свободи може бути підібрана до однієї з глобальних ступенів загальної проблеми. За допомогою огляду на рис. 15 ми можемо сформувати наступну таблицю, яка відображає локальні та глобальні числа:

місцевий	глобальний, елемент 1	глобальний, елемент 2
1	1	3
2	2	4
3	3	4
4	4	6

Використовуючи цю таблицю, ми бачимо, наприклад, що друга ступінь свободи для елемента 2 є четвертою ступенем свободи в глобальній системі нумерації, а третя локальна ступінь свободи відповідає п'ятій глобальній мірі свободи. Звідси значення в другому рядку і третьому стовпці матриці жорсткості елемента 2, позначені\(k_{23}^{(2)}\), слід додати в положення в четвертому рядку і п'ятому стовпці 6 глобальної матриці жорсткості\(\times\) 6. Ми пишемо це як

\[k_{23}^{(2)} \to K_{4,5}\nonumber\]

Кожна з шістнадцяти позицій в матриці жорсткості кожного з двох елементів повинна бути додана в глобальну матрицю відповідно до відображення, заданого таблицею. Це дає результат

\[K = \begin{bmatrix} k_{11}^{(1)} & k_{12}^{(1)} & k_{13}^{(1)} & k_{14}^{(1)} & 0 & 0 \\ k_{21}^{(1)} & k_{22}^{(1)} & k_{23}^{(1)} & k_{24}^{(1)} & 0 & 0 \\ k_{31}^{(1)} & k_{32}^{(1)} & k_{33}^{(1)} + k_{11}^{(2)} & k_{34}^{(1)} + k_{12}^{(2)} & k_{13}^{(2)} & k_{14}^{(2)} \\ k_{41}^{(1)} & k_{42}^{(1)} & k_{43}^{(1)} + k_{21}^{(2)} & k_{44}^{(1)} + k_{22}^{(2)} & k_{23}^{(2)} & k_{24}^{(2)} \\ 0 & 0 & k_{31}^{(2)} & k_{32}^{(2)} & k_{33}^{(2)} & k_{34}^{(2)} \\ 0 & 0 & k_{41}^{(2)} & k_{42}^{(2)} & k_{43}^{(2)} & k_{44}^{(2)} \end{bmatrix}\nonumber\]

Ця матриця попередньо множить вектор вузлових переміщень згідно з рівнянням 2.1.9 для отримання вектора зовнішніх прикладених вузлових сил. Повні системні рівняння, з урахуванням відомих сил і переміщень, потім

\[10^3 \begin{bmatrix} 25.0 & -43.3 & -25.0 & 43.0 & 0.0 & 0.00 \\ -43.3 & 75.0 & 43.3 & -75.0 & 0.0 & 0.00 \\ -25.0 & 43.3 & 50.0 & 0.0 & -25.0 & -43.30 \\ 43.3 & -75.0 & 0.0 & 150.0 & -43.3 & -75.00 \\ 0.0 & 0.0 & -25.0 & -43.3 & 25.0 & 43.30 \\ 0.0 & 0.0 & -43.3 & -75.0 & 43.3 & 75.00 \end{bmatrix} \left \{ \begin{array} 0 \\ 0 \\ 0 \\ u_4 \\ 0 \\ 0 \end{array} \right \} = \left \{ \begin{array} f_1 \\ f_2 \\ f_3 \\ -1732 \\ f_5 \\ f_5 \end{array} \right \}\nonumber\]

Зверніть увагу, що або сила, або зміщення для кожного ступеня свободи відомі, при цьому супутні зміщення або сила невідомі. Тут невідомий лише один з переміщень (\(u_4\)), але в більшості проблем невідомі переміщення значно перевершують невідомі сили. Зауважте також, що тільки ті елементи, які фізично пов'язані з заданим вузлом, можуть сприяти зусиллям цього вузла. У більшості випадків це призводить до глобальної матриці жорсткості, яка містить багато нулів, відповідних вузловим парам, які не охоплюються елементом. Ефективні комп'ютерні реалізації скористаються перевагами розрідженості матриці для економії пам'яті та скорочення часу виконання.

У великих задачах матричні рівняння вирішуються для невідомих переміщень і сил за допомогою гаусового скорочення або інших методів. У цій двоелементній задачі рішення для єдиного невідомого зміщення можна записати майже з огляду. Перемноживши четвертий ряд системи, ми маємо

\[0 + 0 + 0 + 150 \times 10^3 u_4 + 0 + 0 = -1732\nonumber\]

\[u_4 = -1732/150 \times 10^3 = -0.01155 \ in\nonumber\]

Тепер будь-яку з невідомих сил можна отримати безпосередньо. Наприклад, множення першого рядка дає

\[0 + 0 + 0 + (43.4) (-0.0115) \times 10^3 + 0 + 0 = f_1\nonumber\]

\[f_1 = -500 \ lb\nonumber\]

Негативний знак тут вказує на горизонтальну силу на глобальному вузлі #1 знаходиться вліво, протилежному напрямку, передбаченому на малюнку 15.

Процес циклічності через кожен елемент для формування матриці жорсткості елемента, складання матриці елемента в правильні позиції в глобальній матриці, рішення рівнянь для переміщень, а потім зворотне множення для обчислення сил, і друк результатів може бути автоматизований, щоб зробити дуже універсальний комп'ютерний код.

Більшого масштабу ферми (та інших) кінцевих елементів аналіз найкраще проводити за допомогою спеціального комп'ютерного коду, а відмінний для вивчення методу доступний з Інтернету за адресою (https://web.archive.org/web/20060108...urceforge.net/). Цей код, названий фетром, був автором Джейсона Гобата та Даррена Аткінсона для освітнього використання, і включає в себе ряд нових функцій для сприяння зручності користувачів. Повна інформація, що описує цей код, а також джерело мови C і ряд пробних запусків і допоміжного модуля коду доступна на їх веб-сторінках. Якщо у вас є доступ до робочих станцій X-window, також доступна графічна оболонка з назвою velvet.

Приклад\(\PageIndex{7}\)

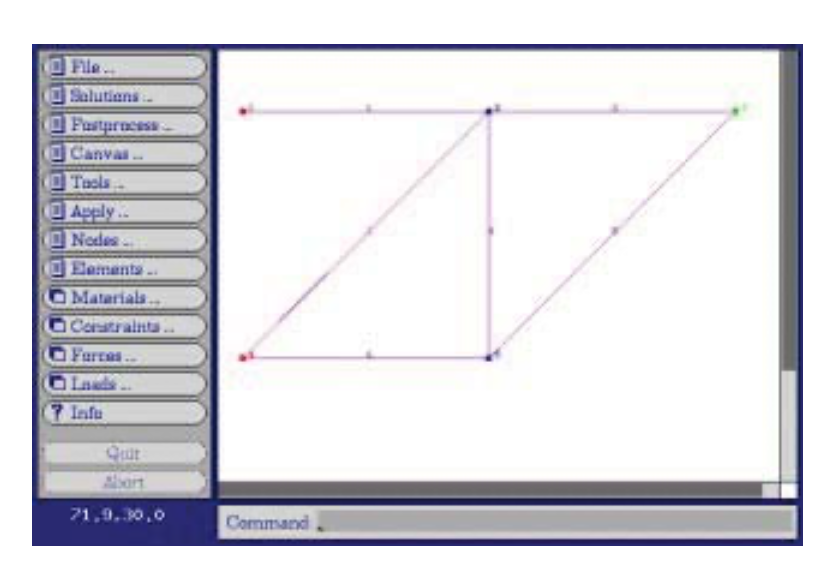
Щоб проілюструвати, як цей код працює для дещо більшої проблеми, розглянемо шестиелементну ферму на малюнку 4, проаналізовану раніше як спільним підходом до аналізу вільного тіла, так і методом Кастільяно. Ферма перемальовується на малюнку 16 оксамитовим графічним інтерфейсом.

Вхідний набір даних, який може бути написаний вручну або розроблений графічно в оксамиті, використовує методи синтаксичного аналізу, щоб спростити те, що може бути дуже нудним і схильним до помилок крок в аналізі скінченних елементів. Набір даних для цієї 6-елементної ферми:

Малюнок 16: Шестиелементна ферма.

problem description
nodes=5 elements=6

nodes
1 x=0 y=100 z=0 constraint=pin
2 x=100 y=100 z=0 constraint=planar 
3 x=200 y=100 z=0 force=P
4 x=0 y=0 z=0 constraint=pin
5 x=100 y=0 z=0 constraint=planar

truss elements
1  nodes=[1,2] material=steel
2  nodes=[2,3]
3  nodes=[4,2]
4  nodes=[2,5]
5  nodes=[5,3]
6  nodes=[4,5]

material properties 
steel E=3e+07 A=0.5

distributed loads

constraints
free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u 
pin Tx=c Ty=c Tz=c Rx=u Ry=u Rz=u 
planar Tx=u Ty=u Tz=c Rx=u Ry=u Rz=u

forces
P Fy=-1000

end 

Сенс цих рядків повинен бути досить очевидним при огляді, хоча для більш докладної інформації слід звернутися до повстяної документації. Вихід, вироблений фетром для цих даних, такий:

**  **
Nodal Displacements
----------------------------------------------------------------
Node #    DOF 1      DOF 2    DOF 3    DOF 4    DOF 5    DOF 6
----------------------------------------------------------------
  1           0          0        0        0        0        0
  2    0.013333   -0.03219        0        0        0        0 
  3        0.02  -0.084379        0        0        0        0
  4           0          0        0        0        0        0
  5  -0.0066667  -0.038856        0        0        0        0


Element Sress
-----------------------------------------------------
1:            4000
2:            2000
3:         -2828.4
4:            2000
5:         -2828.4
6:           -2000
Material Usage Summary 
-------------------------- 
Material: steel
Number:   6
Length:   682.8427
Mass:     0.0000
 
Total mass: 0.0000 

Зверніть увагу, що вертикальне зміщення вузла 3 (значення DOF 2) становить -0.0844, таке ж значення, отримане раніше в прикладі\(\PageIndex{3}\). На малюнку 17 показаний оксамитовий графічний вихід для прогинів ферми (значно збільшений).

Вправа\(\PageIndex{1}\)

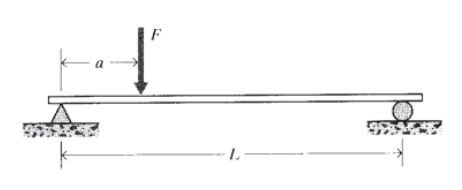
Жорстка балка довжини\(L\) спирається на дві опори, що чинить опір вертикальному руху, і навантажується\(F\) вертикальною силою на відстані a від лівої опори. Намалюйте схему вільного тіла для

балки, замінюючи\(R_1\) опори силами реакції і\(R_2\) які вони чинять на

промінь. Вирішуйте для сил реакції в плані\(F, a\), і\(L\).

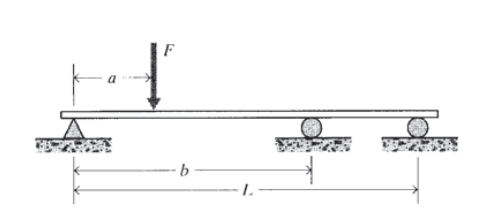
Вправа\(\PageIndex{2}\)

Третя опора додається до балки попередньої задачі. Намалюйте діаграму вільного тіла для цього випадку та запишіть рівняння рівноваги, доступні для вирішення сил реакції на кожній опорі. Чи можна вирішити для всіх сил реакції?

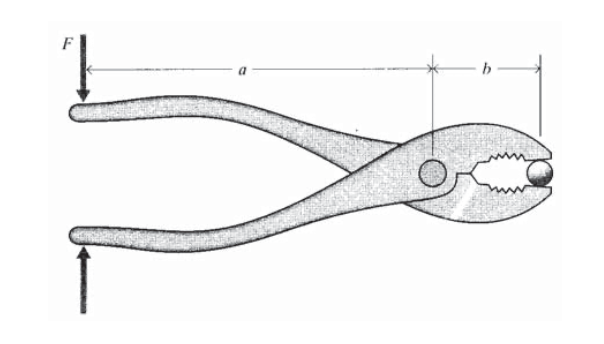
Вправа\(\PageIndex{3}\)

Ручки плоскогубців стискаються з силою F Намалюйте схему вільного тіла для одного з рук плоскогубців. Яка сила, що чиниться на предмет, захоплений між гранями плоскогубців?

Вправа\(\PageIndex{4}\)

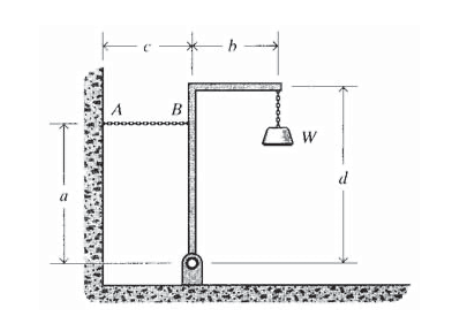
Об'єкт ваги\(W\) підвішується на кадрі, як показано на малюнку. Яке напруження в тросі перепідготовки\(AB\)?

Вправа\(\PageIndex{5}\)

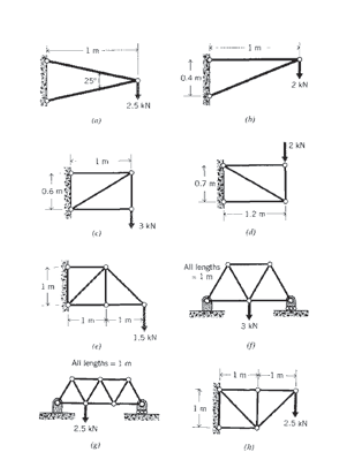
(а) - (h) Визначте зусилля в кожному елементі ферм, намальованих нижче.

Вправа\(\PageIndex{6}\)

(а) - (h) Використовуючи геометричні міркування, визначте відхилення точки навантаження (точки, в яку прикладається навантаження, у напрямку навантаження) для ферм у виконанні вправи\(\PageIndex{5}\). Всі елементи виготовлені з круглих прутків з вуглецевої сталі діаметром 20 мм.

Вправа\(\PageIndex{7}\)

(a) - (h) Те саме, що і вправа\(\PageIndex{6}\), але з використанням теореми Кастільяно.

Вправа\(\PageIndex{8}\)

(a) - (h) Те саме, що і\ (\ pageIndex {6}\, але з використанням аналізу скінченних елементів.

Вправа\(\PageIndex{9}\)

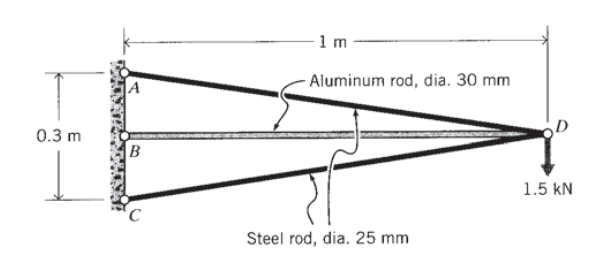
Знайдіть зусилля елемента і прогин в точці навантаження для показаної ферми, використовуючи метод за власним вибором.

Вправа\(\PageIndex{10}\)

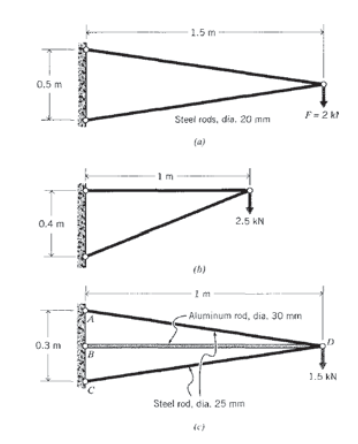
(a) - (c) Випишіть глобальні матриці жорсткості для ферм, перерахованих нижче, і вирішіть для невідомих сил і переміщень.

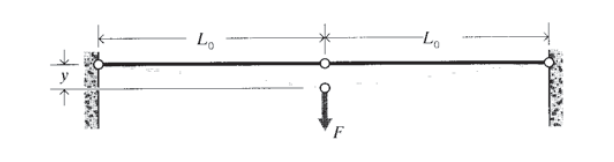
Вправа\(\PageIndex{11}\)

Два кроквяних елемента однакової початкової довжини\(L_0\) з'єднуються горизонтально. Припускаючи, що елементи залишаються лінійно пружними при всіх деформаціях, визначають відхилення вниз\(y\) як функцію навантаження,\(F\) прикладеної поперечно до суглоба.