5.1: Загальна рецептура

Last updated
Save as PDF

Page ID: 32812

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Порівняно з класичною теорією пучків з нескінченно малою деформацією, теорія помірно великих відхилень вносить зміни в відношення деформації-зміщення і вертикальну рівновагу, але залишає конституційне рівняння і горизонтальну рівновагу без змін. Кінематичне відношення, Рівняння (1.9.5) набуває тепер нового терміну завдяки скінченним обертанням елемента балки.

\[\epsilon^{\circ} = \frac{du}{dx} + \boxed{\frac{1}{2} \left(\frac{dw}{dx}\right)^2} − \text{ new term} \label{5.1.1}\]

Визначення кривизни має також нелінійний термін обертання.

\[\kappa = -\frac{\frac{d^2w}{dx^2}}{\left[ 1+ \left(\frac{dw}{dx}\right)^2\right]^{3/2}} \label{5.1.2}\]

Квадрат схилу може бути великим, порівняно з терміном\(\frac{du}{dx}\) і повинен зберігатися в Equation\ ref {5.1.1}. При цьому квадрати нахилу (обертання балки) невеликі в порівнянні з одиницею. Чому? Це пояснюється на малюнку (\(\PageIndex{1}\)), де квадрат схилу наноситься проти схилу.

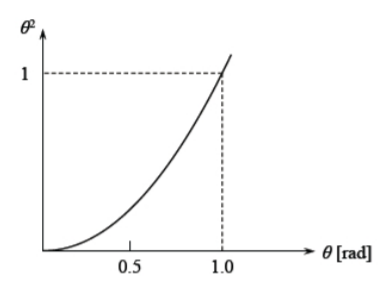
5.1.1.PNG — Малюнок\(\PageIndex{1}\): Значення квадрата терміна схилу.

При\( = 57\) градусах\(\theta = 1\) rad два слова в знаменнику рівняння\ ref {5.1.2} рівні. Однак теорія помірно великих прогинів дійсна до\(\theta = 10^{\circ} \approx 0.175\) рад. Термін\(\theta^2\) становить\(0.03\), що мізерно мало в порівнянні з єдністю. Тому кривизна визначається так само, як і в теорії малих прогинів.

\[\kappa = -\frac{d^2w}{dx^2}\]

У главі 2 було показано, що на рівняння рівноваги в горизонтальному напрямку не впливає кінцеве обертання. Тому ми робимо висновок з Рівняння (2.7.4), що осьова сила або постійна, або нульова

\[N = \text{ constant}\]

Вертикальна рівновага, задана рівнянням (3.79), має новий нелінійний член

\[\frac{d^2M}{dx^2} + \boxed{N\frac{d^2w}{dx^2}}^{-\text{new term}} +q = 0\]

Нарешті, на закон пружності не впливає кінцеве обертання.

\[N = EA\epsilon^{\circ}\]

\[M = EI\kappa\]

Розв'язок пов'язаної задачі залежить від граничних умов в горизонтальному напрямку. Посилаючись на рис. 4.1.1, необхідно розглянути два випадки:

Випадок 1, промінь вільно ковзати,\(N = 0, \; u \neq 0\).
Корпус 2, балка фіксована,\(u = 0, \; N \neq 0\).