2.3: П'єзоелектричні пристрої
- Page ID
- 29579
Чи можемо ми викликати поляризацію матеріалу в ізоляторі таким чином, що не передбачає застосування напруги? Якщо так, то цей метод може зарядити конденсатор, і ми можемо розрядити конденсатор, як зазвичай, для отримання електроенергії. Будь-який пристрій, який виконує це завдання, є пристроєм перетворення енергії. П'єзоелектричні, піроелектричні та електрооптичні пристрої включають цей тип перетворення енергії, і всі вони в даний час доступні як датчики та інші продукти. У п'єзоелектричних пристроях, розглянутих в даному розділі, механічне напруження викликає поляризацію матеріалу.
Якщо на матеріал буде чинити досить велике навантаження, кристалічна структура зміниться. Наприклад, при досить високій температурі і тиску вугілля кристалізується в алмаз, а коли тиск видаляється, матеріал залишається в алмазній формі. Сталь може бути загартована шляхом багаторазового удару по ній в процесі, який називається дробеструйним. Значна кількість енергії необхідна для постійної зміни кристалічної структури матеріалу. У цьому розділі ми не обговорюємо цей ефект. Натомість ми обговорюємо ефект, який зазвичай вимагає мало енергії. При впливі механічної деформації на п'єзоелектричний пристрій встановлюється поляризація матеріалу. Валентні електрони зміщуються, але ядра матеріалу і інші електрони не рухаються. Коли ми знімаємо напругу, матеріальна поляризація йде.
Постійна п'єзоелектрична деформація
Ми можемо описати поляризацію матеріалу п'єзоелектричного ізоляційного матеріалу, включивши термін, який залежить від застосованого механічного навантаження, [25].
\[\overrightarrow{P} =\overrightarrow{D} - \epsilon_0\overrightarrow{E} +d\overrightarrow{\varsigma} \label{2.3.1} \]
У цьому рівнянні\(\overrightarrow{P}\) полягає поляризація матеріалу в\(\frac{C}{m^2}\),\(\overrightarrow{D}\) є зміщення щільності потоку в\(\frac{C}{m^2}\),\(\epsilon_0\) є діелектричною проникністю вільного простору в\(\frac{F}{m}\),\(\overrightarrow{E}\) є прикладеною напруженістю електричного поля в\(\frac{V}{m}\),\(d\) є п'єзоелектричної деформацією постійної в \(\frac{m}{V}\), і\(\overrightarrow{\varsigma}\) це стрес в паскалі. Стрес можна давати і в інших одиницях.
\[1 Pa =1 \frac{J}{m^3} = 1 \frac{N}{m^2} \nonumber \]
Для багатьох матеріалів п'єзоелектрична постійна деформації\(d\) дорівнює нулю, а для багатьох інших матеріалів\(d\) - досить мала. Титанат барію використовується для виготовлення п'єзоелектричних датчиків, оскільки він має відносно великий п'єзоелектричний коефіцієнт деформації,\(d \approx 3 \cdot 10^{-10} \frac{m}{V}\) [25, с. 408]. Додаткові приклади коефіцієнтів наведені в наступному розділі таблиці 3.1.1.
Механічна деформація - це безодинична міра відхилення або деформації, тоді як напруга має одиниці паскалів. Без зовнішнього електричного поля ці величини пов'язані модулем пружності Юнга, який має одиниці\(\frac{N}{m^2}\). \[ \text{strain} =( \frac{1}{\text{Young's elastic modulus}}) \cdot \text{stress} \nonumber \]
Якщо також застосовується електричне поле, напруга і деформація пов'язані\[ \text{strain} =( \frac{1}{\text{Young's elastic modulus}} ) \cdot \text{stress} + \overrightarrow{E} \cdot d \nonumber \]
де\(d\) - постійна п'єзоелектричної деформації. Енергія, що зберігається в п'єзоелектричному пристрої під напругою\(\overrightarrow{\varsigma}\), дається\[E = |\overrightarrow{\varsigma}| \cdot A \cdot l \cdot \eta_{eff} \nonumber \]
де\(A\) - площа поперечного перерізу пристрою в\(m^2\),\(l\) - деформація в м, і\(\eta_{eff}\) є ККД. Пристрої, які більші, деформуються більше, або виготовляються з матеріалів з більшими п'єзоелектричними константами, зберігають більше енергії.
Відповідно до Equation\ ref {2.3.1} поляризація матеріалу ізолюючого кристала лінійно пропорційна прикладеному напруженню. Хоча це точно описує багато матеріалів, це поганий опис інших матеріалів. Для інших п'єзоелектричних кристалів поляризація матеріалу пропорційна квадрату прикладеного напруги.\[ |\overrightarrow{P}| = |\overrightarrow{D}| - \epsilon_0 |\overrightarrow{E}| + d |\overrightarrow{\varsigma}| + d_{quad} {|\overrightarrow{\varsigma}|}^2 \label{2.3.6} \]
де\(d_{quad}\) інша п'єзоелектрична константа деформації. Для моделювання поляризації матеріалу в інших матеріалах необхідні терміни, що включають вищі сили напруги.
П'єзоелектрика в кристалічних матеріалах
Щоб зрозуміти, які матеріали є п'єзоелектричними, потрібно ввести деяку термінологію опису кристалів. Кристалічні матеріали можуть складатися з елементів, таких як\(\text{Si}\), або сполуки, такі як\(\text{NaCl}\). За визначенням атоми в кристалах розташовані періодично. Для опису розташування атомів в кристалі задано дві складові: решітка і основа [25, с. 4]. Решітка - це періодичний масив точок у просторі. \(\mathfrak{n}\)-мірна решітка задається\(\mathfrak{n}\) гратчастими векторами для цілого числа\(\mathfrak{n}\). Ми можемо отримати від однієї точки решітки до кожної іншої точки решітки, переміщаючи ціле число векторів решітки. Три вектори\(\overrightarrow{a_1}\),\(\overrightarrow{a_2}\), і\(\overrightarrow{a_3}\) використовуються для опису фізичних решіток у трипросторі. Вибір векторів решітки не є унікальним. Вектори решітки, які максимально короткі, називаються примітивними гратчастими векторами. Клітинка решітки - це площа (2D) або об'ємна (3D), утворена гратчастими векторами. Примітивна комірка - це площа або обсяг, утворений примітивними гратчастими векторами, і це найменша можлива повторювана одиниця, яка описує решітку.
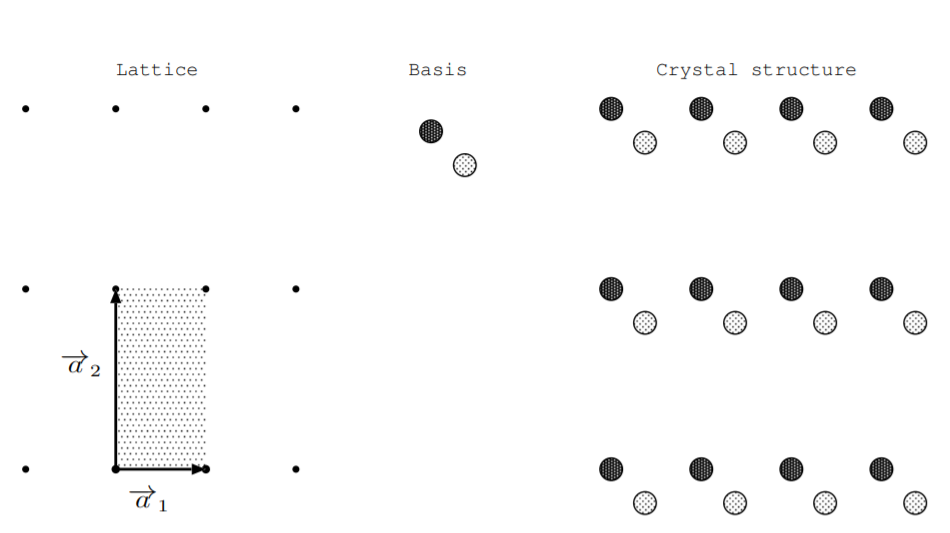
Щоб вказати структуру матеріалу, ми приєднуємо один або кілька атомів до кожної точки решітки. Таке розташування атомів називається кристалічною основою. Решітка і кристалічна основа разом визначають кристалічну структуру [25]. \(\PageIndex{1}\)На малюнку показаний двовимірний приклад решітки, кристалічної основи та кристалічної структури. Оскільки цей приклад є двомірним, для зазначення решітки потрібні лише два вектори решітки. Показано два примітивні вектори решітки, а примітивна комірка затінена.
Існує 14 можливих тривимірних типів решіток, і вони називаються гратами Браве [25]. Кожна з цих можливих решіток має описову назву. \(\PageIndex{2}\)На малюнку показано чотири можливі решітки Браве: проста кубічна, кубічна кубічна, кубічна, кубічна з центром обличчя та асиметрична триклініка. У простій кубічній решітці всі кути між відрізками ліній, що з'єднують найближчі сусідні точки, є прямими кутами, а всі довжини між найближчими сусідніми точками рівні. У асиметричній триклінічної решітці жоден з цих кутів не є прямим кутом, і жодна з цих довжин між найближчими сусідніми точками не дорівнює. \(\PageIndex{2}\)На малюнку показані осередки решітки, але осередки для кубічних решіток, центрованих на тілі, та кубічних решіток з центром обличчя не є примітивними клітинами, оскільки можна знайти менші повторювані одиниці
Розглянемо деякі приклади решіток і кристалічних структур. Кристалічна структура хлориду натрію, наприклад, включає в себе грань центровану кубічну решітку і основу, що складається з одного натрію і одного атома хлору. Іншим прикладом є кремній, який кристалізується в так званій структурі алмазу [25]. Ця кристалічна структура включає кубічну решітку, орієнтовану на грань, і основу, що складається з двох атомів кремнію, в місці (0, 0, 0) і\((\frac{l}{4},\frac{l}{4},\frac{l}{4})\) де\(l\) довжина примітивної комірки. Вуглець\(\text{Si}\)\(\text{Ge}\), і\(\text{Sn}\) всі кристалізуються в цій алмазній структурі з довжиною осередків\(l\) = 0,356, 0,543, 0,565 і 0,646 нм відповідно [25].
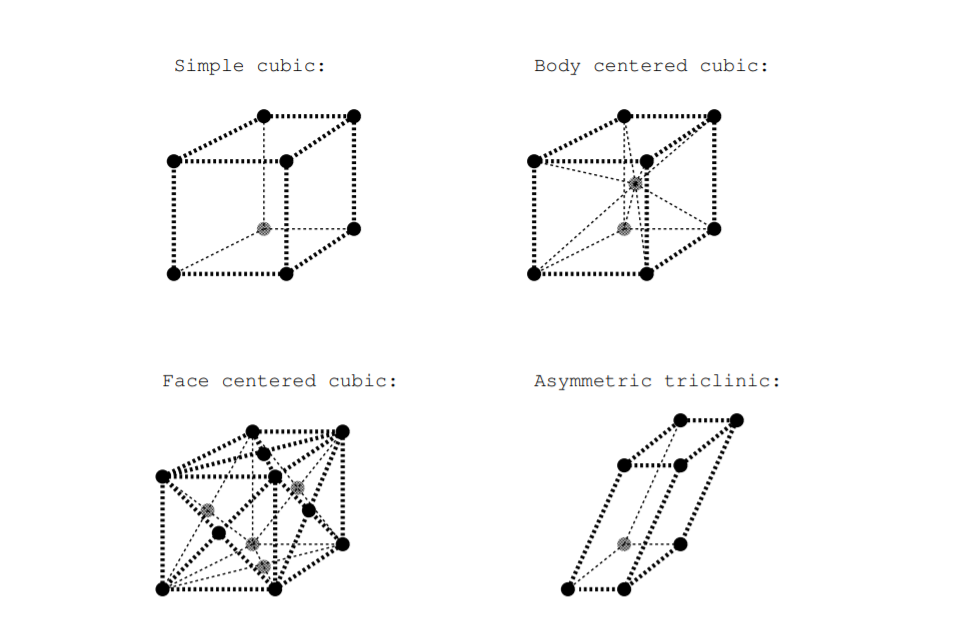
Малюнок\(\PageIndex{2}\): Ілюстрація деяких грат Браве.
Хоча існує лише 14 можливих тривимірних решіток, існує значно більше можливих кристалічних структур, оскільки кристалічна структура також включає основу. Перерахувати всі можливі кристалічні структури не представляється можливим. Натомість вони класифікуються на основі симетрії, яку вони містять. Можливими операціями симетрії є 2-кратні, 3-кратні, 4-кратні та 6-кратні обертання, горизонтальні та вертикальні дзеркальні площини та інверсія. Кристалічні структури групуються на основі елементів симетрії, які вони містять в класах, які називаються групами кристалічних точок. Існує 32 можливі групи кристалічних точок, і вони наведені в табл\(\PageIndex{1}\).
Деякі автори класифікують кристалічні структури на групи кристалічного простору замість груп кристалічних точок [6] [26]. Хоча існує 32 групи кристалічних точок, існує 230 кришталевих космічних груп. Групи кришталевих просторів засновані на трансформаціях симетрії, які можуть включати не тільки обертання та дзеркальні площини, але й комбінацію перекладів разом з обертаннями та дзеркальними площинами. Кришталеві космічні групи не будуть обговорюватися далі в цьому тексті.
| Герман-Могуїн позначення | Позначення Шунфлі | Кришталева система | Кути примітивної гратчастої комірки | Довжини примітивної комірки решітки | П'єзоелек., Електрооптика Поккельса, Без інверсійної симетрії | Піроелектричний |
|---|---|---|---|---|---|---|
| 1 | \(C_1\) | триклініка | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a \neq b \neq c\) | у | у |
| \(\bar{1}\) | \(S_2\) | триклініка | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a \neq b \neq c\) | п | п |
| 2 | \(C_2\) | моноклінічний | \( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \) | \(a \neq b \neq c\) | у | у |
| \(m\) | \(C_{1h}\) | моноклінічний | \( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \) | \(a \neq b \neq c\) | у | у |
| \(\frac{2}{m}\) | \(C_{2h}\) | моноклінічний | \( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \) | \(a \neq b \neq c\) | п | п |
| 222 | \(D_2, V\) | орторомбічний | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a \neq b \neq c\) | у | п |
| 2 мм | \(C_{2v}\) | орторомбічний | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a \neq b \neq c\) | у | у |
| \(\frac{2}{m}\frac{2}{m}\frac{2}{m}\) | \(D_{2h}, V_h\) | орторомбічний | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a \neq b \neq c\) | п | п |
| 4 | \(C_4\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | у | у |
| \(\bar{4}\) | \(S_4\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | у | п |
| \(\frac{4}{m}\) | \(C_{4h}\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | п | п |
| 422 | \(D_4\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | у | п |
| \(4mm\) | \(C_{4v}\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | у | у |
| \(\bar{4}2m\) | \(D_{2d}, V_d\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | у | п |
| \(\frac{4}{m}\frac{2}{m}\frac{2}{m}\) | \(D_{4h}\) | тетрагональні | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b \neq c\) | п | п |
| 3 | \(C_3\) | тригональний | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a = b = c\) | у | у |
| \(\bar{3}\) | \(S_6\) | тригональний | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a = b = c\) | п | п |
| 32 | \(D_3\) | тригональний | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a = b = c\) | у | п |
| \(3m\) | \(C_{3v}\) | тригональний | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a = b = c\) | у | у |
| \(\bar{3}\frac{2}{m}\) | \(D_{3d}\) | тригональний | \( \alpha , \beta , \gamma \neq 90^{\circ} \) | \(a = b = c\) | п | п |
| 6 | \(C_6\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | у | у |
| \(\bar{6}\) | \(C_{3h}\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | у | п |
| \(\frac{6}{m}\) | \(C_{6h}\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | п | п |
| 622 | \(D_6\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | у | п |
| \(6mm\) | \(C_{6v}\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | у | у |
| \(\bar{6}m2\) | \(D_{3h}\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | у | п |
| \(\frac{6}{m}\frac{2}{m}\frac{2}{m}\) | \(D_{6h}\) | шестикутний | \( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \) | \(a = b \neq c\) | п | п |
| 23 | \(T\) | кубічний (ізометричний) | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b = c\) | у | п |
| \(\frac{2}{3}\bar{m}\) | \(T_h\) | кубічний (ізометричний) | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b = c\) | п | п |
| 432 | \(O\) | кубічний (ізометричний) | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b = c\) | у | п |
| \(\bar{4}3m\) | \(T_d\) | кубічний (ізометричний) | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b = c\) | у | п |
| \(\frac{4}{m}\bar{3}\frac{2}{m}\) | \(O_h\) | кубічний (ізометричний) | \( \alpha , \beta , \gamma = 90^{\circ} \) | \(a = b = c\) | п | п |
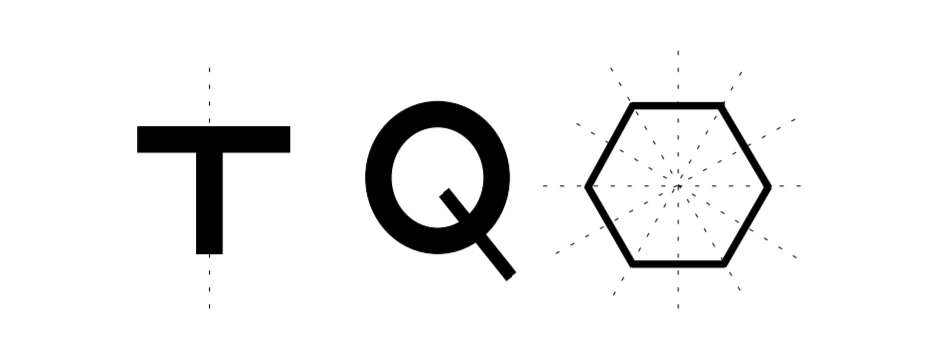
Як приклад ідентифікації елементів симетрії розглянемо 2D фігури на малюнку\(\PageIndex{3}\). Т-подібна фігура має один елемент симетрії, дзеркальну площину симетрії. Форма виглядає однаково, якщо вона відбивається над дзеркальною площиною, зображеною на малюнку пунктиром. Q-форма не має елементів симетрії. Шестикутник має кілька елементів симетрії. Він містить 2-кратне обертання, оскільки воно виглядає однаково при обертанні\(180^{\circ}\). Він також має 3-кратну та 6-кратну симетрію обертання, оскільки вона виглядає однаково при\(60^{\circ}\) обертанні\(30^{\circ}\) відповідно. Він також має кілька дзеркальних площин, показаних пунктирними лініями на малюнку. У цьому прикладі ідентифікуються елементи симетрії 2D форм, але матеріалознавці зацікавлені у виявленні симетрій тривимірних кристалічних структур, щоб отримати уявлення про властивості матеріалів. Матеріали класифікуються на категорії, звані групами кристалічних точок на основі симетрій їх кристалічних структур.
Ми узагальнюємо про кристалічні матеріали на основі того, чи має їх кристалічна структура інверсійною симетрією. Що таке операція інверсії? У 2D інверсія така ж, як обертання на\(180^{\circ}\). У 3D форма або кристалічна структура містить інверсійну симетрію, якщо вона ідентична при обертанні\(180^{\circ}\) та перевернутому через початок [24, с. 269]. Більш конкретно, намалюйте вектор\(\overrightarrow{V}\) від центру фігури до будь-якої точки на поверхні. Якщо фігура має інверсійну симетрію\(\overrightarrow{V}\), то для будь-якого такого вектора точка відстань\(\overrightarrow{V}\) від початку знаходиться також на поверхні фігури. Приклад ліворуч від малюнка\(\PageIndex{4}\) має інверсійну симетрію, оскільки для будь-якого такого вектора\(\overrightarrow{V}\) від центру фігури до точки на поверхні є точка на поверхні, вектор,\(\overrightarrow{V}\) віддалений від початку. Приклад праворуч не містить інверсійної симетрії, як ілюструється вектором,\(\overrightarrow{V}\) показаним стрілкою.
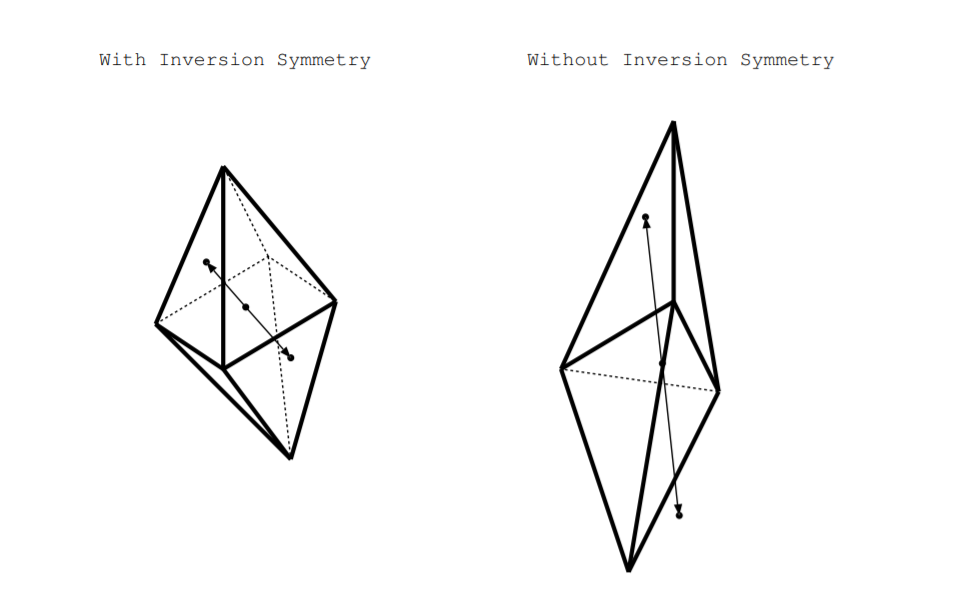
Якщо кристалічна структура має інверсійну симетрію, ми говоримо, що кристал має центр симетрії, інакше ми говоримо, що він нецентросиметричний. Кристалічні структури класифікуються на класи, які називаються групами кристалічних точок, а двадцять одна з 32 точкових груп не мають центру симетрії, тому не містять інверсійної симетрії [24, с. 35]. Двадцять з цих кристалічних точок груп мають полярну вісь, деякі осі в кристалі з різними формами на протилежних кінцях осі. Ці двадцять одна кришталева точка групи вказані як нецентросиметричні в шостому стовпці таблиці\(\PageIndex{1}\). Якщо ми механічно напружимо ці матеріали вздовж полярної осі, різна кількість зарядів буде накопичуватися з різних сторін осі. Діелектричні кристалічні матеріали, кристалічна структура яких належить до будь-якої з цих 21 з цих нецентросиметричних кристалічних точкових груп, є п'єзоелектричними [24].
Таблиця\(\PageIndex{1}\) перераховує всі групи кристалічних точок і підсумовує, чи можуть кристалічні матеріали, кристалічна структура яких належить кожній групі, бути п'єзоелектричними, піроелектричними та електрооптичними. Піроелектрика і електрооптика розглянуті в наступному розділі. Інформація в таблиці надходить з посилань [24] [26] [27] [28]. У лівих двох стовпцях наведено 32 можливі групи кришталевих точок. Існує два різних, але рівнозначних, способи маркування груп кристалічних точок. Перший стовпець називає групи кристалічних точок за допомогою позначення Германна-Могвіна. Це позначення датується 1930-ми роками і використовується хіміками, мінералогами, деякими фізиками. Другий стовпець називає групи кристалічних точок за допомогою нотації Schoenflies. Позначення Шенфлі датується 1891 роком [29], і використовується вона математиками, спектроскопістами та іншими фізиками.
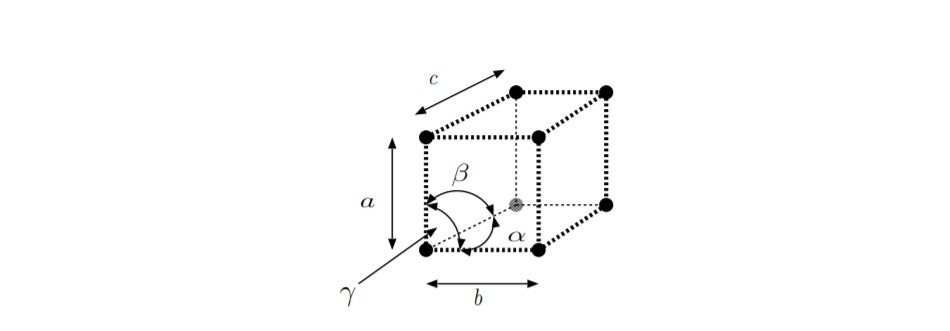
У третьому стовпці таблиці\(\PageIndex{1}\) наведено кристалічну систему. Як показано на малюнку\(\PageIndex{5}\): кути примітивної осередку решітки маркуються\(\alpha,\)\(\beta,\) і\(\gamma\), а довжини сторін маркуються\(a,\)\(b,\) і\(c\). Групи кристалічних точок можна класифікувати на основі кутів і довжин примітивної комірки решітки, яка належить до цієї групи. Література містить кілька тонко різних способів визначення кристалічних систем [30]. Інформація в третьому стовпці слідує за посиланням [28]. Четвертий стовпець дає відносини між кутами примітивної осередку. П'ятий стовпець дає співвідношення між довжинами сторін примітивної осередку. Комбінації кутів і довжин не є унікальними для конкретного ряду. Наприклад, класи\(C_2\) і\(C_{1h}\) обидва мають\(\alpha = 90^{\circ} ,\)\(\beta \neq 90^{\circ} ,\)\(\gamma = 90^{\circ}\), і\(a \neq b \neq c\). Однак кристалічні структури, що належать до цих кристалічних точкових груп, містять різні елементи симетрії. Детальніше про те, які саме елементи симетрії містяться в якій групі кристалів точки, див. [24] [26] [27] [28]. У шостому стовпці вказано, чи має група кришталевих точок інверсійної симетрії. Кристалічні структури без інверсійної симетрії або центру симетрії, звані нецентросиметричними, є як п'єзоелектричними, так і електрооптичними. Останній стовпець перераховує, чи можуть кристалічні матеріали, кристалічна структура яких належить до різних груп кристалічних точок, бути піроелектричними.
Можна почати з кристалічної структури матеріалу, вивести елементи симетрії, які він містить, вивести, чи є матеріал п'єзоелектричним, і вивести, чи є матеріал піроелектричним. Крім того, можна вивести, по яких осях може відбуватися п'єзоелектрика або піроелектрика в матеріалі. Однак цей висновок виходить за рамки цієї книги. Детальніше див. [6] [27] [28] [31].
Щоб передбачити, чи є діелектричний кристалічний матеріал п'єзоелектричним, ідентифікуйте його решітку та кристалічну основу, щоб ідентифікувати його кристалічну структуру. Визначте симетрії кристалічної структури, щоб класифікувати її кристалічну структуру на певну групу кристалічних точок. Якщо ця кристалічна структура містить інверсійну симетрію, матеріал може бути п'єзоелектричним. Нам часто не доводиться проходити всі ці кроки, оскільки група кристалічних точок для багатьох кристалічних матеріалів зведена в таблицю [32]. Навіть якщо кристалічна структура матеріалу містить інверсійну симетрію, п'єзоелектричний ефект та коефіцієнт п'єзоелектричної деформації\(d\) можуть бути занадто малими для вимірювання.
Ефект може виникнути тільки тоді, коли ви напружуєте матеріал вздовж якоїсь певної осі, і це може не виникати при механічному напруженні довільної орієнтації щодо напрямку осей кристалів. Існує лише одна група кристалічних точок, звана асиметричною триклінікою, де випадкове напруження буде виробляти поляризацію матеріалу [24]. Для всіх інших груп точок тільки напруги по певних осях будуть виробляти поляризацію матеріалу [24]. Крім того, у більшості кристалів задана величина напруги вздовж однієї осі кристала буде виробляти різну кількість поляризації матеріалу, ніж та ж кількість напружень, застосованих уздовж різної кристалографічної осі. Якісно стиснення кристала уздовж однієї осі може викликати більший зсув заряду, ніж стиснення кристала по іншій осі. З цієї причини більш точно розглядати п'єзоелектричний коефіцієнт деформації як матрицю. Ця матриця 3х6 має елементи\[d_{ik} =\left. \left(\frac{\partial\text{strain along k}}{\partial\text{electric field along i}}\right)\right|_{\text{for a given stress}} \nonumber \]
де електричне поле має\(x,\)\(y,\) і\(z\) компоненти, а напруга може бути застосована вздовж\(xx,\)\(xy,\)\(xz,\)\(yy,\)\(yz,\) або\(zz\) напрямків.
П'єзоелектрика в аморфних і полікристалічних матеріалах та сегнетоелектриці
У попередньому розділі розглядалися п'єзоелектрики в кристалах. Ми можемо обговорити симетрії кристалічної структури кристалічних матеріалів, але ми не можемо навіть визначити кристалічну структуру для аморфних матеріалів. Однак можна зробити п'єзоелектричні прилади з полікристалічних і аморфних матеріалів. У діелектриках, якщо застосувати зовнішнє електричне поле, індукується поляризація матеріалу. Електричні диполі утворюються тому, що електрони і ядра атомів трохи зміщуються один від одного. Закон Кулона говорить нам, що накопичення заряду, такі як ці електричні диполі, індукують електричне поле. Отже, якщо застосувати зовнішнє електричне поле до діелектрика, цей первинний ефект індукує поляризацію матеріалу, і ця поляризація матеріалу, як вторинний ефект, індукує додаткову поляризацію матеріалу в матеріалі. Як тільки один атом поляризується, утворюючи електричний диполь, сусідні атоми поляризуватимуться. Невеликі області тієї ж поляризації матеріалу називаються електричними доменами.
У деяких діелектричних матеріалах зовнішнє механічне напруження індукує локальну поляризацію матеріалу. Накопичення заряду цього матеріалу поляризації індукує поляризацію матеріалу в прилеглих атомах, що утворюють електричні домени [23]. Цей п'єзоелектричний ефект може виникнути незалежно від того, чи є вихідний матеріал кристалічним, аморфним або полікристалічним [23]. У некристалічних матеріалах цей ефект обов'язково нелінійний, тому ці матеріали недостатньо добре описані рівняннями\ ref {2.3.1} або\ ref {2.3.6}.
Нелінійний процес поляризації матеріалу одного атома, що індукує матеріальну поляризацію сусідніх атомів, що спричиняє утворення електричних доменів, називається сегнетоелектричністю. Сегнетоелектричні матеріали можуть бути кристалічними, аморфними або полікристалічними. У наступному розділі ми побачимо, що матеріали можуть бути сегнетоелектричними піроелектричними та сегнетоелектричними електрооптичними на додаток до сегнетоелектричних п'єзоелектричних. Сегнетоелектричний ефект обмежується температурою. Для багатьох сегнетоелектричних матеріалів ці ефекти відбуваються лише нижче певної температури, званої температурою Кюрі. При нагріванні матеріалів вище температури Кюрі сегнетоелектричний ефект йде [33]. Поляризація матеріалу сегнетоелектричного матеріалу може залежати від того, чи була раніше індукована поляризація матеріалу. Якщо стан матеріалу залежить від його минулої історії, ми говоримо, що матеріал має гістерезис. Сегнетоелектричні матеріали можуть мати поляризацію матеріалу навіть при відсутності зовнішнього механічного напруження або електричного поля, якщо раніше застосовувався джерело енергії.
Хоча префікс ферро- означає залізо, більшість сегнетоелектричних матеріалів не містять заліза, а більшість залізовмісних матеріалів не є сегнетоелектричними. Слово сегнетоелектрик використовується як аналогія зі словом феромагнітний. Деякі залізосодержащие матеріали є феромагнітними. Якщо зовнішнє магнітне поле застосовується через феромагнітний матеріал, в матеріалі встановлюється внутрішнє магнітне поле. Феромагнітні матеріали можуть мати постійний магнітний диполь навіть при відсутності прикладеного магнітного поля. Ми можемо змоделювати електричний диполь як пару зарядів. Ми можемо змоделювати магнітний диполь як невеликий струмовий контур. Феромагнітні матеріали демонструють гістерезис, і вони мають магнітні домени, де магнітні диполі вирівняні.
Спочатку п'єзоелектричний сегнетоелектричний матеріал має випадково вирівняні електричні домени та відсутність поляризації чистого матеріалу, тому він починається як ні п'єзоелектричний, ні сегнетоелектричний. Процес змушення матеріалу проявляти п'єзоелектрику та сегнетоелектрику називається полюванням. Щоб полюс матеріалу, помістіть його в сильне зовнішнє електричне поле [23], наприклад, поперек полюсів батареї, звідси і термін. Полірування не змінює атомну структуру, тому якщо матеріал спочатку був аморфним, він залишиться аморфним. Під час цього процесу утворюються електричні домени, і ці домени залишаються навіть при видаленні зовнішнього поля. Матеріал, який є п'єзоелектричним завдяки цьому виду полюсів, іноді називають електретом [15, с. 297]. Після того, як матеріал полірується, він може мати чисту поляризацію матеріалу на всьому протязі. Крім того, після полірування він є п'єзоелектричним та сегнетоелектричним, тому зовнішнє механічне напруження індукує поляризацію матеріалу локально та у всьому матеріалі.
Матеріали, що використовуються для виготовлення п'єзоелектричних пристроїв
Що робить хорошим матеріалом для п'єзоелектричного датчика або пристрою перетворення п'єзоелектричної енергії? Спочатку п'єзоелектричні пристрої виготовляються з електричних ізоляторів. Коли зовнішня напруга подається на провідник, валентні електрони видаляються з їх атомів, тому ніяка поляризація матеріалу не накопичується. По-друге, п'єзоелектричні пристрої виготовляються з матеріалів з великими п'єзоелектричними константами деформації. Константа п'єзоелектричної деформації настільки мала, що її неможливо виявити у багатьох кристалах з кристалічними структурами з однієї з 21 груп кристалічних точок, які відомі як п'єзоелектричні, і вона дорівнює нулю в кристалах з інших груп кристалічних точок. По-третє, п'єзоелектричні пристрої повинні бути виготовлені з матеріалів, які не є крихкими, щоб вони могли витримувати багаторазові навантаження без постійних пошкоджень. Теплові властивості також можуть бути важливими [33]. Немає матеріалу, який найкраще підходить у всіх додатках.
Кварц, кристалічний\(\text{SiO}_2\), був першим матеріалом, в якому вивчалося п'єзоелектрику. П'єр і Жак Кюрі відкрили ефект кварцу в 1880-х роках [3]. Сьогодні багато п'єзоелектричні пристрої, в тому числі і кварцові генератори, виготовляються з кварцу. Титанат цирконію свинцю - ще один матеріал, який використовується через його відносно високої п'єзоелектричної постійної деформації [3] [34]. У додатках, що вимагають гнучкості і здатності витримувати багаторазові механічні навантаження без пошкоджень, використовуються полімери типу полівінілденфториду [25]. П'єзоелектрику також вивчали в матеріалах, включаючи титанат барію\(\text{BaTiO}_3\), ніобат літію, турмалін.
\[\text{(Na,Ca)(Li,Mg,Al)}_3 \text{(Al,Fe,Mn)}_6 ( \text{BO}_3)_3 (\text{Si}_6\text{O}_8)\text{(OH)}_4 , \nonumber \]
і сіль Рошель
\[\text{KNaC}_4\text{H}_4\text{O}_6 \cdot 4\text{H}_2\text{O} \nonumber \]
[3] [23] [24] [34].
Виробники п'єзоелектричних пристроїв не часто маркують свою продукцію, щоб сказати, виготовлені вони з кристалічних, аморфних або полікристалічних матеріалів, але є переваги та недоліки різних типів матеріалів. Перевагою виготовлення п'єзоелектричних пристроїв з полікристалічних або аморфних матеріалів є те, що пристрої можуть бути легше виготовлені в різних формах, таких як циліндри і сфери [33]. Однак використовувані матеріали часто мають більш низькі температури плавлення, більш високі коефіцієнти розширення температури і більш крихкі [33]. Кристалічні матеріали, такі як кварц, мають переваги бути твердішими і мають більш високу температуру плавлення [33].
Застосування п'єзоелектрики
Ряд електричних компонентів передбачає п'єзоелектрику. При подачі напруги на шматок п'єзоелектричного матеріалу він механічно згинається і деформується. Коли напруга звільняється, вона пружиниться назад на природній резонансній частоті. Цей матеріал може бути інтегрований зі схемою зворотного зв'язку для отримання коливань з точною частотою. Електричні генератори цього типу часто виготовляють з кристалічного кварцу. Більш свіже застосування - п'єзоелектричний трансформатор. Ці прилади використовуються в люмінесцентних лампах з холодним катодом, які використовуються в якості підсвічування для РК-панелей [23, с. 289]. Лампи вимагають близько тисячі вольт для включення і сотні вольт під час використання. Трансформатори з магнітів і котушок можуть досягти цих високих напруг, але п'єзоелектричні трансформатори набагато менше, досить малі, щоб їх можна було встановити на друкованій платі. Традиційний трансформатор включає пару котушок, і він перетворює електрику змінного струму в магнітну енергію в електрику змінного струму при різній напрузі. Аналогічно, п'єзоелектричний трансформатор також включає в себе кілька процесів перетворення енергії. У такому пристрої електрика змінного струму перетворюється в механічні коливання і потім в електрику змінного струму при різній напрузі. Енергія зберігається в цих пристроях, тому вони можуть видавати високі напруги при малих струмах. На малюнку\(\PageIndex{6}\): показаний п'єзоелектричний трансформатор, здатний перетворювати вхід 8 в 14 В на вихід до 2 кВ [35]. На малюнку\(\PageIndex{7}\): показаний приклад деяких дрібних компонентів п'єзоелектричних ланцюгів. Починаючи у верхньому лівому куті та йдучи за годинниковою стрілкою, показано мікрофон, ультразвуковий передавач та приймач, датчик вібрації та генератор.
Ефективність пристроїв перетворення енергії важко обговорювати, оскільки кожен автор робить різні припущення. Однак за будь-якою мірою ККД комерційного п'єзоелектричного пристрою низький, часто 6% і менше [36]. Завдяки такому низькому ККД в якості датчиків використовуються багато п'єзоелектричні пристрої. Незалежно від цього низького ККД, для заготівлі енергії використовуються інші пристрої. Наприклад, одна залізнична станція вбудовує п'єзоелектричні пристрої в платформи для вироблення електроенергії. П'єзоелектричні пристрої також використовувалися для перетворення енергії від руху рідини або від вітру безпосередньо в електрику [36].


Існує інтерес до використання п'єзоелектричних пристроїв для біомедичних застосувань. Кварц є п'єзоелектричним, і він міцний, легко доступний і нетоксичний. Інженери розробили п'єзоелектричні пристрої, призначені для використання поза тілом і для імплантації всередину тіла. Деякі п'єзоелектричні пристрої використовуються в якості датчиків. Наприклад, п'єзоелектричні датчики можуть контролювати коліна або інші суглоби [3]. Також ультразвукова візуалізація є поширеною діагностичною методикою. П'єзоелектричні прилади використовуються як для генерації ультразвукових коливань, так і для їх виявлення [33]. Інші біомедичні п'єзоелектричні пристрої використовуються як джерело електричної енергії. Штучні серця, кардіостимулятори та інші пристрої вимагають електрики, і вони часто обмежені технологією батареї, доступною для постачання енергії [36]. П'єзоелектричні генератори не мають рухомих частин для зносу, і вони можуть уникнути проблеми необхідності зміни батарей. Фізичні навантаження можна класифікувати як безперервні, такі як дихання, або переривчасті, такі як ходьба. Обидва види фізичних навантажень можуть використовуватися як джерело механічної енергії для п'єзоелектричних приладів [36]. Кількість потужності, необхідної для різних біомедичних приладів, варіюється зовсім небагато. Наприклад, штучному серцю може знадобитися близько 8 Вт, тоді як кардіостимулятор може вимагати лише кілька мікроват [36]. П'єзоелектричні пристрої можуть уловлювати енергію від типових фізичних навантажень і перетворювати її в електричну енергію для живлення пристрою. П'єзоелектричний пристрій в штучному коліні виробляв 0,85 мВт [36], а пристрій у взутті генерував 8,4 мВт від ходьби [36].
П'єзоелектричні пристрої використовуються в інших типах систем візуалізації, крім біомедичних систем візуалізації. Одне з більш ранніх застосувань було в гідроакустичних системах. Приблизно за часів Першої світової війни військові активно розробляли гідроакустичні системи для виявлення човнів і підводних човнів. Сьогодні гідролокатори використовуються для виявлення риб і вимірювання глибини водойм [33]. Сонар візуалізації також використовується для аналізу електричних ланцюгів і для виявлення недосконалостей і тріщин в сталі і в зварних швах [33].
П'єзоелектричні пристрої використовуються і в безлічі інших застосувань. П'єзоелектричні датчики використовуються в деяких кнопках і клавіатурах [36]. П'єзоелектричні прилади використовуються для виготовлення акселерометрів [37, с. 353], і вони використовуються для вимірювання витрати труб [33]. Динаміки, мікрофони та зумери можуть бути виготовлені з п'єзоелектричних пристроїв, і вони можуть працювати як на аудіо, так і на ультразвукових частотах. П'єзоелектричні пристрої, які генерують ультразвукові сигнали, можуть використовуватися для емульгування барвників, фарб і харчових продуктів, таких як арахісове масло [33]. Також вони використовуються в деяких запалюваннях гриля барбекю, де механічне напруження викликає електричну іскру [23, гл. 15].
