2.2: Конденсатори

Поляризація матеріалу

Коли зовнішня напруга подається на ізолятор, заряди розділяються по всьому матеріалу, і це поділ заряду називається поляризацією матеріалу. Поляризацію матеріалу можна визначити більш точно через напруженість електричного поля\(\overrightarrow{E}\) і щільності потоку переміщення\(\overrightarrow{D}\), два векторних поля, які відображаються в рівняннях Максвелла, Рівняння 1.6.3 - 1.6.6. Ці векторні поля пов'язані\[\overrightarrow{D} = \epsilon \overrightarrow{E}. \nonumber \]

Чому ми визначаємо два параметри електричного поля, коли вони просто масштабовані версії один одного? Корисно відокремити опис електричного поля всередині матеріалу від опису поля у вільному просторі. Аналогічно, два векторні поля описують магнітне поле, напруженість магнітного поля\(\overrightarrow{H}\) і щільність магнітного потоку\(\overrightarrow{B}\), і ці поля з'являються в рівняннях Максвелла з тієї ж причини. Поляризація матеріалу\(\overrightarrow{P}\) в одиницях\(\frac{C}{m^2}\) визначається як різниця між електричним полем у матеріалі\(\overrightarrow{D}\) та електричним полем, яке було б присутнім у вільному просторі\(\overrightarrow{E}\). Більш конкретно\[\overrightarrow{P} =\overrightarrow{D}-\epsilon_0 \overrightarrow{E} \nonumber \] або\[\overrightarrow{P} =(\epsilon - \epsilon_0) \overrightarrow{E}. \nonumber \]

Ці вирази включають діелектричну проникність вільного простору\(\epsilon_0\) та діелектричну проникність матеріалу,\(\epsilon\) які були визначені в електромагнітних хвиль і матеріалів.

Вчені перевантажують як слова ємність, так і поляризація множинними значеннями. Докладніше про різні способи використання цих умов див. у Додатку C.

Накопичувач енергії в конденсаторах

Коли конденсатор заряджається, енергія перетворюється з електричної енергії в енергію, що зберігається в поляризації матеріалу, яка є енергією поділу заряду. Коли він розряджається, енергія перетворюється з енергії, що зберігається в поляризації матеріалу назад в електричну енергію протікають електронів. Конденсатори виготовляються з ізоляційного матеріалу між провідними пластинами. У міру подачі напруги на ізоляторі на пластин накопичуються заряди. Накопичена напруга пропорційно заряду, накопиченому на пластин. \[Q =Cv \label{2.2.4} \]

У рівнянні\ ref {2.2.4},\(Q\) є заряд в кулоні,\(v\) є напругою, а константою пропорційності є ємність\(C\) у фарад. Якщо взяти похідну по відношенню до часу, то отримаємо більш звичне вираз, що стосується струму і напруги на конденсаторі. \[\frac{dQ}{dt} =i =C\frac{dv}{dt} \nonumber \]

Ємність конденсатора пов'язана з діелектричної проникністю діелектричного матеріалу між провідниками. Діелектрична проникність - це міра кількості енергії, яка може зберігатися діелектричним матеріалом. Як описано рівнянням 1.6.20, для паралельного пластинчастого конденсатора ця залежність становить\[C =\frac{\epsilon A}{d_{thick}} \label{2.2.6} \]

де\(A\) - площа плит і\(d_{thick}\) - відстань між плитами. Енергія,\(E\) що зберігається в конденсаторі як функція напруги, що подається на нього, задається\[E =\frac{1}{2}Cv^2 =\frac{1}{2}Qv. \nonumber \]

Ємність заповненого вакуумом паралельного пластинчастого конденсатора описується Equation\ ref {2.2.6} з діелектричною проникністю\(\epsilon = \epsilon_0\), діелектричною проникністю вільного простору. У міру того, як ми заряджаємо конденсатор, заряди накопичуються на обкладинках, і ніяких змін вакууму між обкладинками не відбувається. Якщо замінити вакуум діелектриком на\(\epsilon > \epsilon_0\), ємність стає більше. Конденсатор, заповнений діелектриком, може зберігати більше енергії, все інше рівне, тому що діелектричний матеріал змінюється в міру заряду конденсатора. Більш конкретно, матеріал поляризується. У ізоляторі електрони пов'язані зі своїми атомами, і струм не може протікати. Натомість електрони в діелектрику трохи рухаються по відношенню до своїх ядер, залишаючись пов'язаними з атомами. Електрони завжди знаходяться в русі для матеріалів при температурах вище абсолютного нуля, але коли матеріал поляризується, чисте розташування електронів щодо ядер змінюється. У міру заряду конденсатора електрони трохи зміщуються від своїх атомів, врівноважуючи заряди на обкладинках, і більше енергії накопичується в діелектрику при заданій напрузі. Ми говоримо, що цей процес індукує електричні диполі. Чим більше діелектрична проникність\(\epsilon\), тим більше матеріал може накопичувати енергії, поляризуючи таким чином. З цієї причини конденсатори часто заповнені діелектричними матеріалами, такими як діоксид\(Ta_2O_5\) танталу, який має\(\epsilon = 25\epsilon_0\) [18]. Матеріал з\(\epsilon = 25\epsilon_0\), наприклад, зможе зберігати в 25 разів енергію наповненого повітрям конденсатора такого ж розміру з однаковим прикладеною напругою.

Діелектрична проникність та пов'язані з нею заходи

З історичних причин діелектрична проникність може виражатися різними показниками. Електрична сприйнятливість\(\chi_e\), відносна діелектрична проникність\(\epsilon_r\)\(n\), показник заломлення та\(\epsilon\) діелектрична проникність описують здатність матеріалу зберігати енергію в електричному полі. Електрична сприйнятливість - це безодинична міра, пов'язана з діелектричною проникністю\[\chi_e = \frac{\epsilon}{\epsilon_0}-1 \nonumber \]

і відносна діелектрична проникність - це ще одна безодинична міра, визначена\[\epsilon_r = \frac{\epsilon}{\epsilon_0}. \nonumber \]

За допомогою деякої алгебри ми можемо записати поляризацію матеріалу з точки зору відносної діелектричної проникності або електричної сприйнятливості. \[\overrightarrow{P} =(\epsilon_r-1)\epsilon_0\overrightarrow{E} =\epsilon_0\chi_e\overrightarrow{E} \nonumber \]

Вчені, що вивчають оптику, часто використовують показник заломлення, ще одна безодинична міра, яка представляє відношення швидкості світла у вільному просторі до швидкості світла в матеріалі. \[n =\frac{c}{|\overrightarrow{v}|} = \frac{\text{speed of light in free space}}{\text{speed of light in material}} \nonumber \]

Оскільки електромагнітні хвилі не можуть рухатися швидше, ніж швидкість світла у вільному просторі, показник заломлення матеріалу більше одиниці\(n > 1\). Припускаючи, що матеріал є хорошим ізолятором і\(\mu =\mu_0\), які, як правило, є безпечним припущенням для оптики, взаємозв'язок між показником заломлення та діелектричною проникністю спрощує\[n =\sqrt{\epsilon_r}. \nonumber \]

У таблиці\(\PageIndex{1}\) наведено відносні діелектричні можливості деяких ізоляторів, використовуваних для виготовлення конденсаторів або п'єзоелектричних пристроїв. Значення всі наближені. Дивіться наведені посилання для отримання більш детальної інформації.

У визначеннях 1.6.3 і в таблиці\(\PageIndex{1}\) діелектрична проникність трактується як скалярна константа, але в деяких контекстах потрібен більш складний опис. У кристалічному матеріалі напруга, прикладена вздовж однієї кристалографічної осі, може викликати поділ заряду по всьому матеріалу легше, ніж напруга того ж розміру, прикладене вздовж іншої осі.

Таблиця\(\PageIndex{1}\): Орієнтовні значення відносної діелектричної проникності різних матеріалів.

Матеріал	Відносна діелектрична проникність\(\epsilon_r\)	Довідка
Вакуум	\ (\ epsilon_r\) ">1.0	[3]
тефлонові	\ (\ epsilon_r\) ">2.1	[3]
Поліетилен	\ (\ epsilon_r\) ">2.3	[3]
Папір	\ (\ epsilon_r\) ">3.0	[3]
\(\text{SiO}_2\)	\ (\ epsilon_r\) ">3.5	[18]
слюда	\ (\ epsilon_r\) ">6.0	[3]
\(\text{Al}_2\text{O}_3\)	\ (\ epsilon_r\) ">9	[18]
\(\text{AlP}\)	\ (\ epsilon_r\) ">10.2	[9]
\(\text{ZrSiO}_4\)	\ (\ epsilon_r\) ">12.5	[19]
\(\text{Si}\)	\ (\ epsilon_r\) ">11.8	[9]
\(\text{Ge}\)	\ (\ epsilon_r\) ">16	[9]
\(\text{Ta}_2\text{O}_5\)	\ (\ epsilon_r\) ">24	[20]
\(\text{ZrO}_2\)	\ (\ epsilon_r\) ">25	[18]
\(\text{HfO}_2\)	\ (\ epsilon_r\) ">40	[18]
\(\text{TiO}_2\)	\ (\ epsilon_r\) ">50	[18]
\(\text{PbS}\)	\ (\ epsilon_r\) ">161	[9]
\(\text{PbSe}\)	\ (\ epsilon_r\) ">280	[9]
\(\text{BaSrTiO}_3\)	\ (\ epsilon_r\) ">300	[18]
\(\text{PbTe}\)	\ (\ epsilon_r\) ">360	[9]

Малюнок\(\PageIndex{1}\): Ілюстрація поляризації матеріалу.

У таких випадках матеріал називають анізотропним. Діелектрична проникність анізотропних матеріалів більш точно описується матрицею.

\[ \begin{pmatrix} \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{yx} & \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{zx} & \epsilon_{zy} & \epsilon_{zz} \end{pmatrix} \nonumber \]

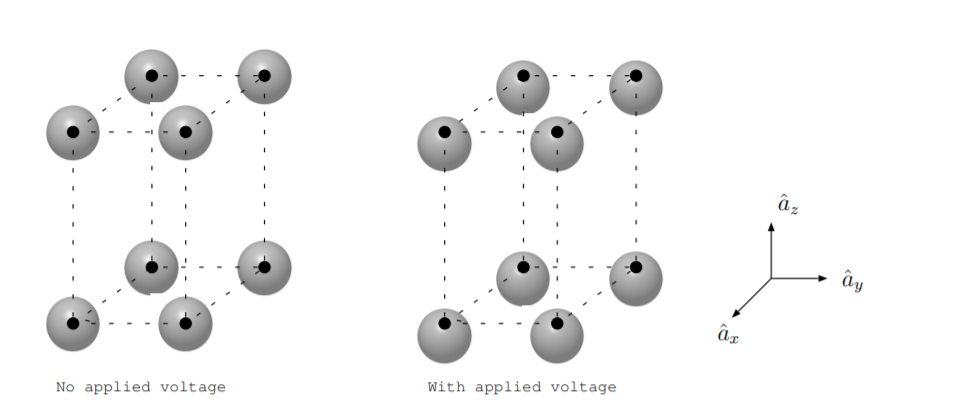
У лівій частині малюнка\(\PageIndex{1}\) зображені деякі атоми кристала. Маленькі чорні кола представляють розташування ядер атомів в кристалах, а сірі кола представляють електронну хмару, що оточує ядра кожного атома. Якщо в\(\hat{a}_z\) напрямку прикладати електричне поле, матеріал поляризується, тому електрони трохи зміщуються щодо ядер, як показано на малюнку праворуч. Оскільки відстань атомів відрізняється в\(\hat{a}_y\) напрямку\(\hat{a}_x\) і, ніж напрямок, зовнішнє поле, необхідне для отримання однакового зміщення заряду, буде відрізнятися в\(\hat{a}_y\) напрямках\(\hat{a}_x\) і, ніж\(\hat{a}_z\) напрямок для цього матеріалу.\(\hat{a}_z\) З цієї причини матеріал, проілюстрований на малюнку, є анізотропним, а діелектрична проникність найкраще описується матрицею на відміну від скалярної величини.

Властивості конденсатора

Конденсатори - це пристрої перетворення енергії, що використовуються в додатках від стабілізації джерел живлення, до фільтрації сигналів зв'язку, до відділення зміщення постійного струму від сигналу змінного струму. Хоча конденсатори та акумулятори зберігають електричну енергію, енергія в акумуляторах зберігається в хімічних зв'язках атомів електродів, тоді як енергія зберігається в конденсаторах в поляризації матеріалу від зв'язаних зарядів, що зміщуються в діелектричному шарі.

Малюнок\(\PageIndex{2}\): Діапазон ємностей і максимальних значень напруги для різних типів конденсаторів, наступні [21] і [22].

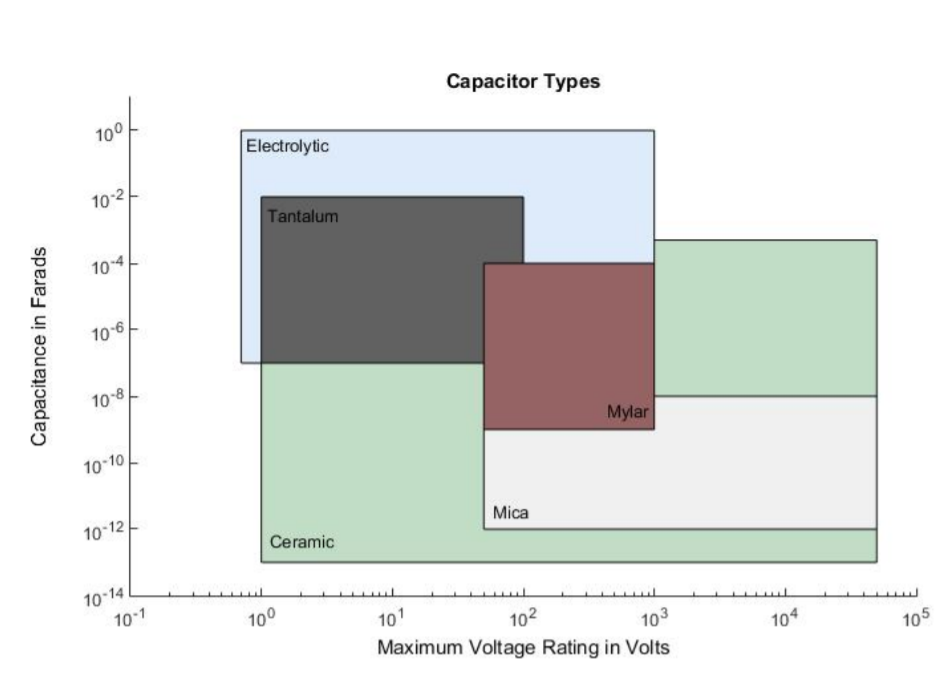
Перші два заходи, які слід враховувати при виборі конденсатора для використання в ланцюзі, - це ємність і максимальна напруга. Конденсатор може пошкодитися, якщо його помістити в ланцюг, де напруга на ньому перевищує максимальне номінальне значення. Приблизні діапазони цих параметрів для конденсаторів з різними діелектричними матеріалами наведені на рис\(\PageIndex{2}\). Діапазони ємності знаходяться на вертикальній осі, а максимальні діапазони напруги - на горизонтальній осі. Наприклад, електролітичні конденсатори часто можна знайти зі значеннями ємності в діапазоні від 1\(10^{-7}\) до 1 F і максимальними номіналами напруги в діапазоні від 1 до 1000 В. Аналогічно, керамічні конденсатори часто можна зустріти зі значеннями ємності від\(10^{-13}\) до\(5 \cdot 10^{-4}\) F і максимальними номіналами напруги в діапазон від 1 до 50 000 В.

Хоча ємність та максимальна напруга є важливими параметрами, які слід враховувати, вони не є єдиними міркуваннями. Ще одним фактором, який слід враховувати, є стабільність температури. В ідеалі ємність буде незалежною від температури. Однак всі матеріали мають ненульовий температурний коефіцієнт. Керамічні та електролітичні конденсатори, як правило, більш чутливі до зміни температури, ніж полімерні або вакуумні конденсатори [22]. Точність, або точність, також важлива. Подібно до того, як резистори маркуються з допусками, конденсатори можуть мати допуски, наприклад,\(\pm5\%\) або\(\pm10\%\). Ще одним фактором, який слід враховувати, є еквівалентний послідовний опір [23, гл. 1]. Всі матеріали мають певний питомий опір, тому всі конденсатори мають деякий кінцевий опір. Для обліку внутрішнього опору ми можемо моделювати будь-який фізичний конденсатор як ідеальний конденсатор послідовно з ідеальним резистором, а значення використовуваного резистора називається еквівалентним послідовним опором. Також слід враховувати витік конденсатора [22]. Якщо конденсатор здатний зберігати свій накопичений заряд протягом тривалого періоду часу, конденсатор має невелику витік. Якщо конденсатор швидко розряджається навіть при відключенні від ланцюга, він має велику витік. Ідеальний конденсатор не має витоку [22]. Конденсатори також диференціюються за терміном експлуатації. Ідеальний конденсатор працює десятиліттями без деградації. Однак деякі типи конденсаторів, наприклад електролітичні конденсатори, не розраховані на тривалий термін служби [22]. Інші фактори, які слід враховувати, включають вартість, доступність, розмір та частотну характеристику [22].

Малюнок\(\PageIndex{3}\): Натуральна слюда.

В якості діелектрика використовується кераміка, скла, полімери та інші матеріали [22]. Часто конденсатори класифікуються за діелектричним матеріалом, який вони містять [22]. Керамічні конденсатори невеликі, дешеві і легко доступні [22]. Вони часто можуть переносити великі прикладені напруги [22]. Зазвичай вони мають невеликі значення ємності, погану точність, погану температурну стабільність і помірну витік [22]. Вони мають низький еквівалентний послідовний опір і витримують великий струм, але можуть викликати перехідні скачки напруги, [23, гл. 1]. Деякі керамічні конденсатори є п'єзоелектричними. Якщо ці конденсатори вібрувати, або навіть постукати олівцем, в ланцюг буде вноситися шум через п'єзоелектрику [23, гл. 12].

Слюда - цікавий матеріал, який використовується як діелектрик в конденсаторах. \(\PageIndex{3}\)На малюнку показана природна слюда, зібрана на шахті Ruggles поблизу Графтона, Нью-Гемпшир. Слюда поставляється в різних природних формах, включаючи біотит і мусковіт\(\text{KAl}_2(\text{AlSi}_3\text{O}_{10})(\text{OH})_2\) [24]. Слюда - це лускатий мінерал з шаруватою структурою [24], тому слюдяні конденсатори можуть бути виготовлені з дуже тонкими діелектричними шарами. Слюдяні конденсатори часто мають хорошу точність і невеликі витоки [22].

Малюнок\(\PageIndex{4}\): Конденсатори розміру наскрізного отвору.

Конденсаторні діелектрики виготовлені з багатьох видів полімерів, включаючи полістирол, полікарбонат, поліестер, поліпропілен, тефлон і майлар [22]. Ці конденсатори часто мають хорошу точність, температурну стабільність і характеристики витоку [22].

Не всі конденсатори мають тверді діелектрики. Вакуум - це діелектрик. Конденсатори з вакуумним діелектриком використовуються в додатках, які передбачають високу напругу або які вимагають дуже низького витоку [22]. Конденсатори з рідкими діелектриками, виготовленими з масла, застосовуються в аналогічних ситуаціях [22]. Електролітичні конденсатори часто мають діелектрики, які представляють собою комбінацію твердих матеріалів з рідкими електролітами. Електроліт - це рідина, через яку деякі заряди можуть тепер легше інших. Електролітичні конденсатори поляризовані, що означає, що вони мають позитивні і негативні висновки, тому, подібно до діода, орієнтація конденсатора в ланцюзі важлива. Усередині електролітичного конденсатора знаходиться з'єднання декількох матеріалів. Початкове застосування напруги на заводі хімічно створює оксидний шар, який є діелектриком. Реверсивний напруга розчинить діелектрик і зруйнує конденсатор. Однією з переваг електролітичних конденсаторів є те, що невеликий прилад може мати велику ємність. Однак часто вони мають погану точність, температурну стабільність і витік [22]. Крім того, електролітичні конденсатори мають кінцевий термін служби, оскільки рідина з часом може деградувати.