4.10: Розсіяний резистор

Last updated
Save as PDF

Page ID: 34543

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Іноді в схемній конструкції нам знадобиться резистор. Зазвичай це робиться або з полі, або з дифузією (показано на малюнку\(\PageIndex{1}\)). Якби ми взяли наш n-бак або подібну дифузію n-типу, ми могли б зробити довгу вузьку смужку і використовувати її як резистор. Поки ми тримаємо підкладку на землі, а будь-які напруги на резисторі більше землі, n-p перехід буде зворотним зміщеним, а резистор буде ізольований від підкладки. Тепер ми всі знаємо, що\[\begin{array}{l} R &= \frac{\rho L}{A} \\ &= \frac{L}{nq \mu tW} \end{array}\]

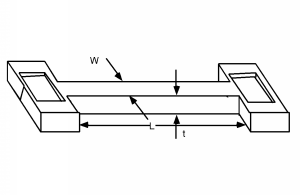Розсіяний резистор, показаний у вигляді довгої тонкої прямокутної призми шириною W, довжиною L і висотою t, що з'єднує два прямокутника.

Єдина біда в тому,\(n\) для чого потрібен дифузійний резистор? Швидкий погляд на діаграму, що показує концентрацію носія як функцію глибини після дифузії показує, що коли ми робимо дифузію,\(n\) це не постійна, але змінюється, коли ми спускаємося в пластину. Нам доведеться зробити якийсь інтеграл, припускаючи багато паралельних тонких резисторів, кожен з різною концентрацією носія! Це не дуже задовільно.

Насправді, це настільки незадовільно, що інженери IC придумали кращий опір опису, ніж той, що включає\(n\) і\(\mu\). Зверніть увагу, що ми могли б написати рівняння\(\PageIndex{1}\) як\[R = \frac{1}{nq \mu t} \frac{L}{W}\]

Першу фракцію (яка містить концентрацію носія, товщину тощо) визначаємо як опір\(R_{s}\) листа дифузії. Хоча це може бути більш-менш прогнозованим, це, як правило, також вимірюване значення після виготовлення. \[R_{s} \equiv \frac{1}{nq \mu t}\]

\(R_{s}\)має одиниці\(\mathrm{"Ohms}/\mathrm{square"}\), і ви, ймовірно, спокуса запитати «на квадрат що?». Ну, це може бути будь-який квадрат взагалі, виміряний в сантиметрах, мікрометрах, кілометрах і т.д., так як все, що нам дійсно потрібно знати, це\(R_{s}\) і відношення довжини до ширини структури резистора, щоб знайти опір резистора. Нам не потрібно знати, які одиниці використовуються для вимірювання довжини та ширини, якщо вони однакові для обох. Наприклад, якщо резистор на малюнку\(\PageIndex{1}\) має лист питомий опір\(50 \ \Omega / \mathrm{square}\), то шляхом блокування резистора на квадрати, які знаходяться\(W\) в обох вимірах, ми бачимо, що резистор має довжину 7 квадратів (рис.\(\PageIndex{2}\)) і тому його опір задається як:\[\begin{array}{l} R &= 50 \ \left(\frac{\Omega}{\mathrm{square}}\right) 7 \ \ (\mathrm{squares}) \\ &= 350 (\Omega) \end{array}\]

Верхня грань резистора з малюнка 1 вище розділена на 7 квадратів, кожен має розмір W як по ширині, так і по довжині.