7.10: Проблеми

Q1. Адіабатичні транзистори

Розглянемо інвертор, показаний нижче.

Малюнок$\PageIndex{1}$: Інвертор з адіабайчним приводом.

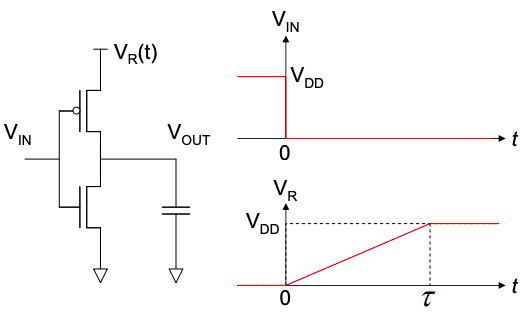
На відміну від звичайного CMOS інвертора, в цьому пристрої напруга живлення$V_{R}$, регулюється під час роботи комутації. Спочатку напруга на вихідному конденсаторі дорівнює нулю, але при t = 0 вхідна напруга падає до нуля. Також при t = 0 напруга живлення зростає від нуля до логічного високої напруги,$V_{DD}$.

Припустимо, що PMOS FET моделюється резистором, R.

(а) Показати, що енергія, що розсіюється під час операції перемикання,

$E = \frac{RC}{\tau} CV_{DD}^{2} \text{ for } \tau \gg RC$

Це відоме як адіабатичний перемикач, оскільки перемикання відбувається (в межі) без розсіювання енергії, тобто ми додаємо заряд до конденсатора за допомогою зникаючої невеликої надлишкової напруги.

[Підказка: Ви можете$V_{OUT}$ припустити форму,$V_{OUT} = a + b\exp[-t/RC] + ct$ де a, b і c є константами, які потрібно визначити.]

(b) Показати також, що розсіюється енергія зменшується до стандартної енергії комутації CMOS$E = \frac{CV_{DD}^{2}}{2} \text{ for } \tau \gg RC$

(c) Наведений вище приклад показує адіабатичне перемикання, коли напруга конденсатора змінюється від низької до високої. Чи можна це реалізувати взагалі? тобто розглянемо випадок, коли напруга конденсатора змінюється від високого до низького. А що відбувається, коли конденсатор не змінює напругу під час циклу?

Q2. Клітинні автомати

Це питання стосується запропонованої архітектури молекулярної електроніки: молекулярних квантово-точкових клітинних автоматів. Цифри малюються з еталонного.

У цій архітектурі інформація зберігається в бістабільних осередках. Приклад осередку наведено нижче:

Малюнок$\PageIndex{2}$: Бістабільна комірка для використання в комп'ютері клітинних автоматів.

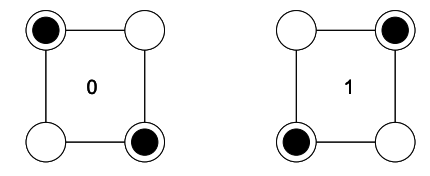
Ця комірка складається з чотирьох електронних пасток, розташованих по кутах квадрата. Залишаються тільки дві пастки. З електростатики є два стабільних стану з електронами на протилежних кутах квадрата.

Для передачі інформації осередки розміщуються в лінію. Потім інформація поширюється електростатично, без протікання струму. Стверджується, що розсіювання потужності таким чином виключається і не потрібні з'єднувальні дроти.

Малюнок$\PageIndex{3}$: Провід стільникових автоматів.

Змінюючи топологію, можна зробити логічні ворота. Наприклад, нижче ми покажемо інвертор.

Малюнок$\PageIndex{4}$: Інвертор стільникових автоматів.

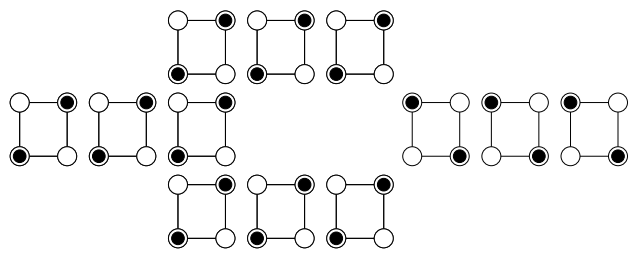
(а) Запропоновані «ворота більшості» показані нижче. Вихід Z - це більшість входів, A, B і C. Тобто якщо входів більше 1, ніж нульових входів, то Z = 1, інакше Z = 0. Використовуйте цей затвор для проектування двох вхідних воріт І.

Малюнок$\PageIndex{5}$: Пропоновані ворота більшості.

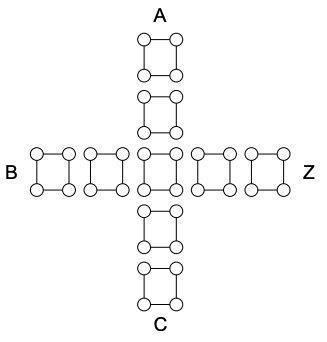
(b) Чи справді ворота більшості бездисипаційні? Підказка: обчислити ентропію до і після рішення більшості.

Довідка: Великий піст, «Обхід транзисторної парадигми» Наука 288 1597 (2004)

Q3. Продукти затримки потужності в нанорозмірах

Продукт затримки потужності - це мінімальна енергія, що розсіюється на біт оброблюваної інформації. Для CMOS інвертора PDP це:

$$PDP = CV^{2} \nonumber$$

де V - напруга живлення, а C - ємність навантаження, як видно інвертором. У цьому питанні будемо вважати, що напруга живлення фіксоване.

(а) Визначте ємність навантаження як функцію затвора та квантових ємностей. Припустимо, ми можемо знехтувати всіма іншими ємностями.

(b) Розглянемо 2d польовий транзистор (де$C_{Q} \rightarrow \infty$). Якщо його розміри масштабуються коефіцієнтом s, як масштабується PDP?

(c) Тепер розглянемо квантовий дротовий польовий транзистор с$C_{Q}\ll C_{G}$. Його ємність затвора задається

$$C_{G}=2\pi \varepsilon \frac{l}{\log(r/a_{0})} \nonumber$$

де$\varepsilon$ - діелектрична постійна ізолятора затвора, l - довжина затвора, r - радіус затвора і$a_{0}$ радіус проводу 1d.

Припустимо, що l і r масштабуються коефіцієнтом s, як працює ємність затвора для квантової дротяної польової транзисторної шкали?

(d) Тепер розглянемо вплив квантової ємності на PDP на квантовий дротовий польовий транзистор. Як працює загальна шкала PDP? Чи масштабування швидше або повільніше, ніж еквівалентний PDP з використанням великих квантових свердловин польових транзисторів?

Q4. Механічні транзистори

Розглянемо механічний вимикач.

Малюнок$\PageIndex{6}$: Механічний вимикач.

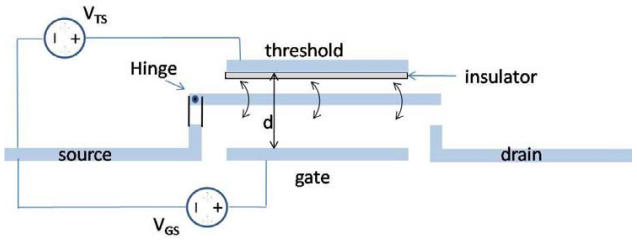
Провідник тягнуть до електрода затвора при$|V_{GS}|>|V_{TS}|$ включенні приладу, і до порогового електрода при$|V_{GS}|<|V_{TS}|$ виключенні приладу. Припустимо, два перемикачі підключені разом в додатковій логічній схемі, яка приводить в дію ємнісне навантаження, як показано нижче.

Малюнок$\PageIndex{7}$: Додаткова логічна схема з механічними вимикачами.

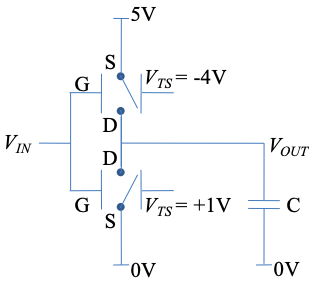
(i) Графік стійкого стану$V_{OUT}$ проти$V_{IN}$, де$V_{IN}$ коливається від 0 до 5 В. Покажіть, що схема взаємодоповнює.

(ii) Припустимо$V_{IN}$, що переключається з 0 В на 5 В, а потім назад на 0V. Скільки енергії розсіюється?

(iii) Розглянемо один з перемикачів. $C_{T}^{ON}$$C_{G}^{ON}$Дозволяти і бути порогово-провідникова ємність, а затвор-провідник ємність, відповідно, у включеному стані, і нехай$C_{T}^{OFF}$ і$C_{G}^{OFF}$ бути ємності, відповідно, в вимкненому стані. Див. Малюнок нижче.

Малюнок$\PageIndex{8}$: Ємнісні моделі вимикача в конфігурації ON і OFF.

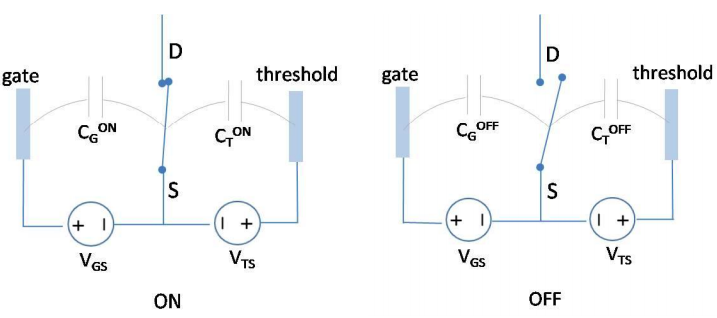
Яка енергія зберігається в цих конденсаторах в (a) ON і в (b) OFF позиціях як функція$V_{GS}$ і$V_{TS}$?

Тепер підключіть N перемикачів все провідні паралельно.

Малюнок$\PageIndex{9}$: N перемикачів всі провідні паралельно.

Кожен вимикач має$V_{TS} = +1V$ і опір,$R=100\Omega$. Припустимо, що всі електроди затвора з'єднані між собою на потенціал$V_{GS}$. Для спрощення аналізу припускаємо, що$C_{G}^{ON} \gg C_{T}^{ON}$ і те$C_{T}^{OFF} \gg C_{G}^{OFF}$. Крім того, візьміть$C_{G}^{ON} = C_{T}^{OFF} = C$.

(iv) Враховуючи статистику Больцмана та різницю потенційних енергій між станами OFF та ON, з N перемикачів, яка ймовірна кількість перемикачів, які увімкнені як функція C,$V_{GS}$ і$V_{TS}$ коли$|V_{GS}|<|V_{TS}|$?

(v) Знайти I для N перемикачів як функцію$V_{GS}$ і$V_{TS}$ for$0 < V_{GS} < 5V$ (for$V_{TS} = 1V$).

(vi) Чи має механічний вимикач якусь користь перед звичайними CMOS?

Q5.

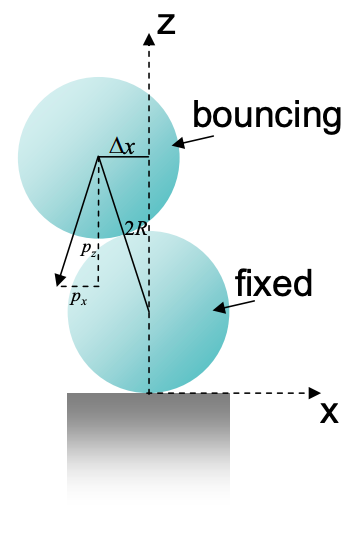
(а) Розглянемо два однакових кульки кожен 1 см в діаметрі і масою m = 1 г. Один тримається нерухомим, а другий опускається прямо на нього з висоти d = 10см. З одного лише принципу невизначеності, яка очікувана кількість разів рухається м'яч відскакує на нерухомому м'ячі, перш ніж він взагалі пропускає останній м'яч? Припустимо, що м'яч скинутий з оптимального початкового стану.

Підказка: деякі частини цієї проблеми можна вирішити класично.

(b) Обговорити наслідки (i) для більярдних куль комп'ютерів.

Малюнок$\PageIndex{10}$: Позацентрове зіткнення між нерухомою кулькою та підстрибуючим м'ячем.

Q6. Наступне питання стосується механічних перемикачів іонного каналу при T = 300K.

а) Припустимо, що будь-який даний іонний канал або відкритий з провідністю$G = G_{0}$, або закритий з провідністю$G = 0$. Використовуючи статистику Больцмана, напишіть вираз для провідності гігантського аксона кальмара (з N іонними каналами паралельно) як функції прикладного мембранного потенціалу, В. Припустимо, що кількість відкритих каналів при$V = 0$ є$N_{0}$.

Підказка: Враховуючи статистику Больцмана, відносні популяції$N_{1}$ та двох$N_{2}$ станів, розділених енергією dU, є$N_{1}/N_{2} = \exp(-dU/kT)$.

б) Там, де це можливо, враховуючи дані на малюнку 7.5.8, оцініть свої параметри.

в) Намалюйте представник IV одного іонного каналу.