7.5: Реверсивні комп'ютери

Last updated
Save as PDF

Page ID: 31928

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

У попередньому розділі ми визначили обчислення як процес, який збільшує інформацію та зменшує невизначеність. Але якщо невпевненість (тобто ентропія) зменшується всередині комп'ютера, ентропія повинна збільшуватися поза комп'ютером. Це застосування другого закону термодинаміки, який стверджує, що всі фізичні системи можуть тільки збільшувати ентропію з часом.

З усіх фізичних законів другий закон термодинаміки славиться тим, що визначає «стрілу часу». Наслідок другого закону полягає в тому, що обчислення є незворотними, принаймні, якщо обчислення змінює невизначеність.

Для прикладу розглянемо два вхідних затвора І. Якщо один з входів на затвор І дорівнює нулю, то інформація в іншому вході викидається. Таким чином, загальна кількість станів зменшується, коли входи поширюються на вихід елемента І. Отже, зменшується ентропія, тепло розсіюється і ворота І не оборотні.

Знімок екрана 2021-05-27 о 15.04.52.png — Малюнок\(\PageIndex{1}\): І ворота не оборотні. Якщо вихід дорівнює нулю, входи не можуть бути реконструйовані.

Тепло, що розсіюється в затворі І, розраховується наступним чином. Існує чотири можливі вхідні стани. Припускаючи, що кожен є рівноймовірним, ентропія Шеннона

\[ H_{in} = -\log_{2} 1/4 = 2 \text{ bits} \nonumber \]

Є два можливих стану виведення. Імовірність виходу X = 0 дорівнює ¾, а ймовірність X = 1 дорівнює ¼.

\[ H_{out} = -\frac{3}{4} \log_{2} 3/4 - \frac{1}{4}\log_{2}1/4 \approx 0.811 \text{ bits} \nonumber \]

Таким чином,

\[ \Delta E = -k_{B} T\ln(2)\Delta H \approx 3.4\times 10^{-21} J \nonumber \]

Але що робити, якщо ми спроектували ворота, які не викидали стани під час обчислень? Така система була б оборотною, і що важливіше, їй не потрібно було б розсіювати енергію.

Фактично запропоновано кілька оборотних логічних елементів. Мабуть, найвідомішим незворотним комп'ютером є більярдний м'яч комп'ютер піонером Фредкіна.

Приклад логічних воріт більярдного кулі наведено на малюнку\(\PageIndex{2}\). Більярдні кулі запускаються в логічні ворота з позицій A і B. Якщо відбувається зіткнення, кулі відхиляються до позицій W і Z. якщо один куля відсутній, однак, вихід на X або Y генерується. Також потрібно припустити, що кулі підкоряються законам класичної механіки, тертя немає і зіткнення ідеально пружні. Зауважимо, що кількість станів в більярдному кулі логічні елементи не змінюється — більярдні кулі не створюються і не руйнуються.

Знімок екрана 2021-05-27 о 15.09.54.png — Малюнок\(\PageIndex{2}\): Ворота зіткнення з двома кульовими. Після Фейнмана, *лекції з обчислень*. Редактори A.J.G. Гей та Р.В. Аллен, Еддісон-Веслі 1996.

Більш складні пристрої можливі шляхом додавання «перенаправлення воріт» (стін). Наприклад, на малюнку\(\PageIndex{3}\) показаний перемикач, зроблений із воріт зіткнення та перенаправлення.

Знімок екрана 2021-05-27 о 15.11.11.png — Малюнок\(\PageIndex{3}\): Більярдний кульовий вимикач. Після Фейнмана, *лекції з обчислень*. Редактори A.J.G. Гей та Р.В. Аллен, Еддісон-Веслі 1996.

Але враховуючи, що багато логічних воріт, таких як і ворота, за своєю суттю нереверсивні, виникає питання: чи може довільний алгоритм бути реалізований повністю з оборотних елементів? Відповідь - так. Реверсивні комп'ютери можуть бути побудовані повністю з фундаментального оборотного елемента, відомого як ворота Фредкіна, показаний на малюнку\(\PageIndex{3}\).

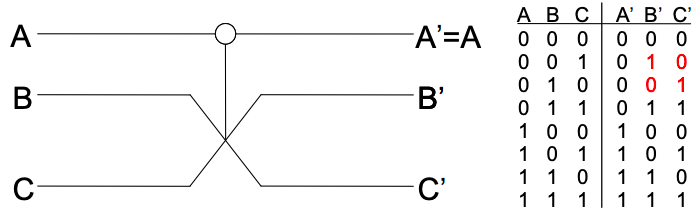
Знімок екрана 2021-05-27 о 15.12.17 — Малюнок\(\PageIndex{4}\): Символ Фредкінських воріт. А є незмінним. Якщо A = 0, то B і C перемикаються. Якщо A = 1, то B і C залишаються незмінними. Всі логічні елементи можуть бути сформульовані з оборотних воріт Фредкіна. Після Фейнмана, *лекції з обчислень*. Редактори A.J.G. Гей та Р.В. Аллен, Еддісон-Веслі 1996.

Реалізація воріт Фредкіна з більярдними кульками показана на малюнку\(\PageIndex{4}\).

Знімок екрана 2021-05-27 о 15.13.13 — Малюнок\(\PageIndex{5}\): Ворота Фредкіна, побудовані з чотирьох вимикачів більярдних кульових. Після Фейнмана, *лекції з обчислень*. Редактори A.J.G. Гей та Р.В. Аллен, Еддісон-Веслі 1996.