Skip to main content
LibreTexts - Ukrayinska

5.3: Розрахунки FET

  1. Last updated
  2. Save as PDF
  • Page ID
    31738

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    На відміну від двох термінальних корпусів, де ми довільно встановлюємо\(E_{F} = 0\) та зміщували потенціали джерела та стоку під зміщенням, конвенція FET фіксує електрод джерела на землі. Є два джерела напруги:\(V_{GS}\), потенціал затвора і\(V_{DS}\), потенціал зливу. Проаналізовано вплив\(V_{GS}\) і\(V_{DS}\) на молекулярний потенціал за допомогою ємнісних дільників і суперпозиції:

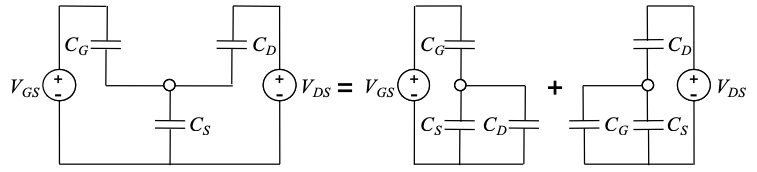
    Скріншот 2021-05-12 о 22.37.14 png
    Малюнок\(\PageIndex{1}\): Аналіз молекулярного транзистора за допомогою ємнісного дільника та суперпозиції.

    \[ U_{E S}=-q V_{G S} \frac{1 /\left(C_{D}+C_{S}\right)}{1 /\left(C_{D}+C_{S}\right)+1 / C_{G}}-q V_{D S} \frac{1 /\left(C_{G}+C_{S}\right)}{1 /\left(C_{G}+C_{S}\right)+1 / C_{D}} \nonumber \]

    Спрощуючи і відзначаючи, що загальна ємність у молекули становить\(C_{ES} = C_{S} + C_{D} + C_{G}\):

    \[ U_{ES} = -qV_{GS}\frac{C_{G}}{C_{ES}}-qV_{DS} \frac{C_{D}}{C_{ES}} \nonumber \]

    Ми також повинні розглянути зарядку. Як і раніше,

    \[ U_{C} = -\frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber \]

    Нагадаємо, що зарядка виступає проти зрушень потенціалу через\(V_{GS}\) або\(V_{DS}\). Таким чином, якщо зарядка значна, напруга комутації збільшується; див. Рис.

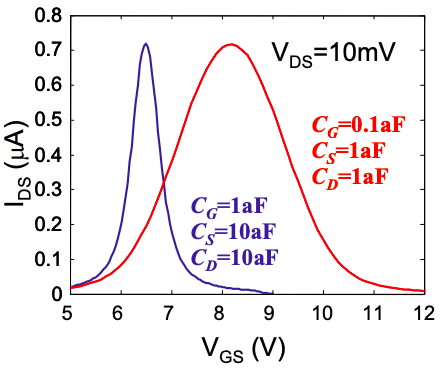
    Скріншот 2021-05-12 о 22.43.20 png
    Малюнок 5.2.1 розрахований під двома різними наборами ємностей. Зарядка важливіша для менших ємностей. Спостерігається, що напруга комутації для цього пристрою збільшується до ~ 8,1 В.

    Додавання статичного потенціалу за рахунок\(V_{DS}\) і\(V_{GS}\) дає, потенціал U в перерахунку на заряд, N і зміщення.

    \[ U=-qV_{GS} \frac{C_{G}}{C_{ES}}-qV_{DS}\frac{C_{D}}{C_{ES}}+\frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber \]

    Ми також маємо вираз для потенціалу для N через U (див. Рівняння (3.7.8))

    \[ N = \int^{\infty}_{-\infty} g(E-U) \frac{\tau_{D}f(E,\mu_{S})+\tau_{S}f(E, \mu_{D})}{\tau_{S}+\tau_{D}} dE \nonumber \]

    Як і раніше, Рівняння (5.3.4) і (5.3.5) зазвичай повинні бути вирішені ітераційно, щоб отримати U. тоді ми можемо вирішити для струму, використовуючи:

    \[ I = q\int^{\infty}_{-\infty} g(E-U)\frac{1}{\tau_{S}+\tau_{D}} \left(f(E,\mu_{S})-f(E,\mu_{D})\right)dE \nonumber \]