7.1: Децибели

Last updated
Save as PDF

Page ID: 32784

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Робота з амплітудою і шкалою децибел.

Шкала децибел виражає амплітуди і значення потужності логарифмічно. Визначення для них відрізняються, але узгоджуються один з одним.

\[power(s,\; in\; decibels)=10\log\frac{power(s)}{power(s_{0})} \nonumber \]

\[amplitude(s,\; in\; decibels)=20\log\frac{amplitude(s)}{amplitude(s_{0})} \nonumber \]

Тут потужність (s ₀) і амплітуда (s ₀) представляють опорну потужність і амплітуду відповідно. Кількісне визначення потужності або амплітуди в децибелах по суті означає, що ми порівнюємо величини зі стандартом або що ми хочемо висловити, як вони змінилися. Ви почуєте такі заяви, як «Сигнал знизився на 3 дБ» і «Коефіцієнт посилення фільтра в смузі зупинки становить -60" (децибели скорочено дБ.).

Вправа\(\PageIndex{1}\)

Приставка «деці» має на увазі десяту; децибел - десята частина Бел. Для кого названа ця міра?

Рішення

Олександр Грехем Белл. Він розробив це, тому що ми, здається, сприймаємо фізичні величини, такі як гучність і яскравість логарифмічно. Іншими словами, для нас має значення відсоток, а не абсолютні відмінності. Ми використовуємо децибели сьогодні, тому що загальні значення є малими цілими числами. Якби ми використовували Bels, вони були б десятковими дробами, які не настільки елегантні.

Послідовність цих двох визначень виникає тому, що потужність пропорційна квадрату амплітуди:

\[power(s)\propto amplitude^{2}(s) \nonumber \]

Підключивши цей вираз до визначення децибел, ми виявимо, що

\[10\log\frac{power(s)}{power(s_{0})}=10\log\frac{amplitude^{2}(s)}{amplitude^{2}(s_{0})}=20\log\frac{amplitude(s)}{amplitude(s_{0})} \nonumber \]

Через таку послідовність констатація відносної зміни в терміні децибел однозначна. Коефіцієнт збільшення амплітуди 10 відповідає збільшенню амплітуди та потужності на 20 дБ!

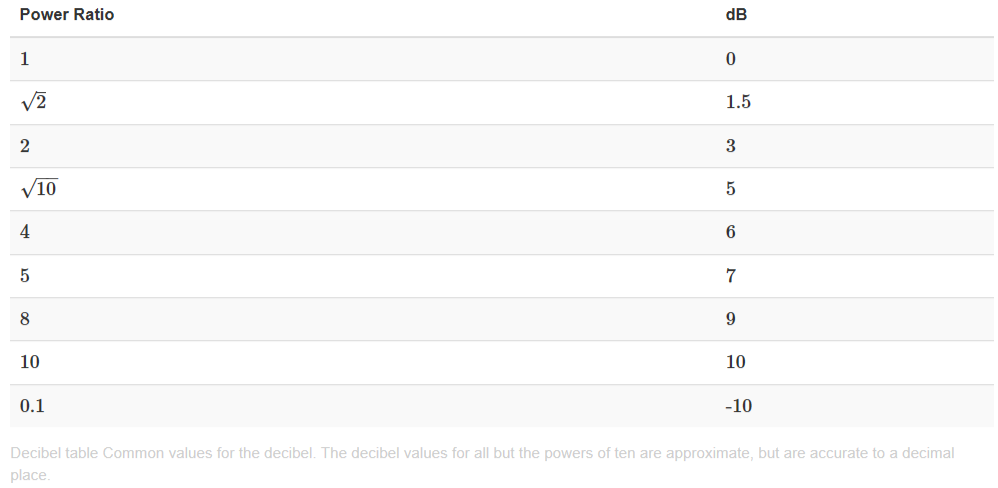
Супровідна таблиця надає «приємні» значення децибел. Перетворення значень децибел назад і вперед - це весело, і перевіряє вашу здатність думати про значення децибел як суми та/або відмінності відомих значень та коефіцієнтів як продуктів та/або коефіцієнтів. Це перетворення спирається на логарифмічну природу децибел шкали. Наприклад, щоб знайти значення децибел для\[\sqrt{2} \nonumber \] ми зменшуємо вдвічі значення децибел для 2; 26 дБ дорівнює 10+10+6 дБ, що відповідає співвідношенню 10×10×4=400. Децибел величини додати; значення співвідношення помножити.

Однією з причин децибел використовується так багато, є співвідношення вхід-вихід частотної області для лінійних систем:

\[Y(f)=X(f)H(f) \nonumber \]

Оскільки функція передачі множить спектр вхідного сигналу, щоб знайти вихідну амплітуду на заданій частоті, ми просто додаємо коефіцієнт посилення фільтра в децибелах (відносно посилання на один) до вхідної амплітуди на цій частоті. Цей розрахунок є однією з причин того, що ми будуємо величину передавальної функції за логарифмічною вертикальною шкалою, вираженою в децибелах.