3.9: Концепція імпедансу

Цілі навчання

• Обговорення результатів, якщо всі джерела в схемі є складними експоненціальними.

Замість того, щоб вирішувати диференціальне рівняння, що виникає в ланцюгах, що містять конденсатори та індуктори, давайте зробимо вигляд, що всі джерела в схемі є складними експоненціальними, що мають однакову частоту. Хоча це притворство може бути лише математично вірним, ця вигадка значно полегшить вирішення схеми незалежно від того, яким джерелом насправді є.

Малюнок 3.9.1 Проста RC-схема

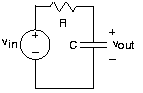
Для наведеного вище прикладу RC ланцюга, нехай

$$v_{in}=V_{in}e^{i2\pi ft} \nonumber$$

Комплексна амплітуда V _в визначає розмір джерела і його фазу. Критичним наслідком припущення, що джерела мають таку форму, є те, що всі напруги і струми в ланцюзі також є складними експоненціальними, мають амплітуди, регульовані KVL, KCL, і v-i відносини і ту ж частоту, що і джерело. Щоб оцінити, чому це повинно бути правдою, давайте досліджуємо, як поводиться кожен елемент ланцюга, коли напруга або струм є складною експоненціальною. Для резистора,

$$v=Ri \nonumber$$

Коли

$$v=Ve^{i2\pi ft} \nonumber$$

Тоді

$$i=\frac{V}{R}e^{i2\pi ft} \nonumber$$

Таким чином, якщо напруга резистора складна експоненціальна, так і струм, з амплітудою

$$I=\frac{V}{R} \nonumber$$ (визначається v-i співвідношенням резистора) і частотою, такою ж, як і напруга. Зрозуміло, що якби струм вважався складним експоненціальним, так було б і напруга. Для конденсатора,

$$i=C\frac{\mathrm{d} v}{\mathrm{d} t} \nonumber$$

Нехай напруга буде складною експоненціальною, ми маємо:

$$i=CVi2\pi fe^{i2\pi ft} \nonumber$$

Амплітуда цієї складної експоненціальної дорівнює:

$$I=CVi2\pi f \nonumber$$

Нарешті, для індуктора, де

$$v=L\frac{\mathrm{d} i}{\mathrm{d} t} \nonumber$$ А

Припускаючи, що струм є складною експоненціальною, призводить до того, що напруга має вигляд:

$$v=LIi2\pi fe^{i2\pi ft} \nonumber$$

Його складна амплітуда задається:

$$V=LIi2\pi f \nonumber$$

імпеданс

Основним наслідком припущення складних експоненціальних напруг і струмів є те, що співвідношення

$$Z=\frac{V}{I} \nonumber$$ для кожного елемента не залежить від часу, а залежить від частоти джерела. Ця величина відома як імпеданс елемента.

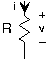
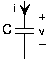
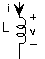
Резистор Z _R = R Конденсатор Z _c = 1/i2 πFC π 2 π 2 Індуктор Z _L = i2 πFL

Малюнок 3.9.2 Імпеданс

Імпеданс - це, як правило, складнозначна, залежна від частоти величина. Наприклад, величина імпедансу конденсатора обернено пов'язана з частотою, і має фазу − π 2 - π/2. Це спостереження означає, що якщо струм складний експоненціальний і має постійну амплітуду, то амплітуда напруги зменшується з частотою.

Розглянемо окружні закони Кірхоффа. Коли напруги навколо петлі всі складні експоненціальні однакової частоти, ми маємо:

$$\sum_{nN}v_{n}=\sum_{nN}V_{n}e^{i2\pi ft}=0 \nonumber$$

що означає

$$\sum_{nN}v_{n}=0 \nonumber$$

складні амплітуди напруг підкоряються КВЛ. Ми можемо легко уявити, що складні амплітуди струмів підкоряються ККЛ.

Ми виявили, що джерело (и), що дорівнює складній експоненціальній однаковій частоті, змушує всі змінні ланцюга бути складними експоненціальними однаковою частотою. Отже, відношення напруги до струму для кожного елемента дорівнює відношенню їх складних амплітуд, яке залежить тільки від частоти джерела і значень елемента.

Така ситуація виникає через те, що елементи схеми лінійні та інваріантні за часом. Наприклад, припустимо, у нас був елемент схеми, де напруга дорівнювало квадрату струму:

$$v(t)=Ki^{2}(t) \nonumber$$

Якщо

$$i(t)=Ie^{i2\pi ft}\\ v(t)=KI^{2}e^{i2\pi 2ft} \nonumber$$

це означає, що напруга і струм більше не мали однакової частоти і що їх співвідношення було залежним від часу.

Оскільки для лінійних елементів ланцюга складна амплітуда напруги пропорційна складній амплітуді струму:

$$V=ZI \nonumber$$

припускаючи складні експоненціальні джерела означає, що елементи схеми поводяться так, ніби вони були резисторами, де замість опору ми використовуємо імпеданс. Оскільки складні амплітуди напруги та струму також підкоряються законам Кірхоффа, ми можемо вирішувати схеми, використовуючи дільник напруги та струму та правила послідовного та паралельного поєднання, вважаючи елементи імпедансами.