3.2: Ідеальні елементи схеми

Last updated
Save as PDF

Page ID: 33145

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Цей модуль надає приклади елементів елементарної схеми; резистора, конденсатора та індуктора, які забезпечують лінійні залежності між напругою та струмом.

Елементарні елементи ланцюга - резистор, конденсатор та індуктор - накладають лінійні відносини між напругою та струмом.

Резистор

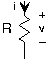
Резистор є далеко і далеко найпростішим елементом схеми. У резисторі напруга пропорційна струму, з постійною пропорційності R, відомою як опір.

\[v(t) = R\, i(t) \nonumber \]

Опір має одиниці Ом, що позначаються Ω, названий на честь німецького вченого-електрика Георга Ома. Іноді v-i відношення для резистора записується i = Gv, при G провідність, рівна 1/R. Провідність має одиниці Siemens (S), і названа на честь німецького промисловця електроніки Вернера фон Сіменса.

Коли опір позитивний, як і в більшості випадків, резистор споживає енергію. Миттєве енергоспоживання резистора можна записати одним з двох способів.

\[p(t) = R\, i^{2}(t) = \frac{1}{R}v^{2}(t) \nonumber \]

Коли опір наближається до нескінченності, ми маємо те, що відомо як розімкнута ланцюг: Ніякого струму не протікає, але ненульова напруга може з'явитися на відкритому ланцюзі. У міру того, як опір стає нульовим, напруга йде до нуля для ненульового потоку струму. Така ситуація відповідає короткому замиканню. Надпровідник фізично реалізує коротке замикання.

Конденсатор

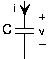
\[i = C\frac{\mathrm{d} v(t)}{\mathrm{d} t} \nonumber \]

Конденсатор зберігає заряд і співвідношення між збереженим зарядом і результуючою напругою q = Cv. Константа пропорційності, ємність, має одиниці фарад (F), і названа на честь англійського фізика-експериментатора Майкла Фарадея. Оскільки струм - це швидкість зміни заряду, v-i відношення може бути виражено в диференціальному або інтегральному вигляді.

\[i(t) = C\frac{\mathrm{d} v(t)}{\mathrm{d} t}\; or\; v(t) = \frac{1}{C}\int_{-\infty }^{t}i(\alpha )d\alpha \nonumber \]

Якщо напруга на конденсаторі постійне, то струм, що протікає в нього, дорівнює нулю. У цій ситуації конденсатор еквівалентний обриву ланцюга. Потужність, що споживається/виробляється напругою, прикладеною до конденсатора, залежить від твору напруги та його похідної.

\[p(t) = Cv(t)\frac{\mathrm{d} v(t)}{\mathrm{d} t} \nonumber \]

Цей результат означає, що сумарні витрати енергії конденсатора до часу t стисло задаються

\[E(t) = \frac{1}{2}Cv^{2}(t) \nonumber \]

Цей вислів передбачає фундаментальне припущення теорії схем: всі напруги і струми в будь-якому ланцюзі в далекому далекому минулому були нульовими (t = - ∞).

Індуктор

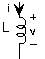
\[v = L\frac{\mathrm{d} i(t)}{\mathrm{d} t} \nonumber \]

Індуктор зберігає магнітний потік, з більшими індукторами, здатними зберігати більше потоку. Індуктивність має одиниці Генріса (H), і названа на честь американського фізика Джозефа Генрі. Диференціальна та інтегральна форми v-i відношення індуктора є

\[v(t) = L\frac{\mathrm{d} i(t)}{\mathrm{d} t}\; or\; i(t) = \frac{1}{L}\int_{-\infty }^{t}v(\alpha )d\alpha \nonumber \]

Потужність, що споживається/виробляється індуктором, залежить від добутку струму індуктора і його похідної

\[p(t) = Li(t)\frac{\mathrm{d} i(t)}{\mathrm{d} t} \nonumber \]

і його загальні витрати енергії до часу

\[E(t) = \frac{1}{2}Li^{2}(t) \nonumber \]

Джерела

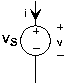
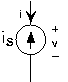
Малюнок 3.2.4 Джерело напруги зліва і джерело струму праворуч схожі на всі елементи ланцюга тим, що вони мають певну залежність між визначеною для них напругою і струмом. Для джерела напруги **v=v _s** для будь-якого струму i, *для джерела струму i **= -i _s** для будь-якої напруги* v

Джерела напруги і струму також є елементами ланцюга, але вони не є лінійними в строгому сенсі лінійних систем. Наприклад, співвідношення v-i джерела напруги дорівнює v=v _s незалежно від того, яким може бути струм. Що стосується джерела струму, то i=-i _sнезалежно від напруги. Інша назва джерела постійної напруги - акумулятор, і його можна придбати в будь-якому супермаркеті. Джерела струму, з іншого боку, набагато складніше придбати; ми дізнаємося, чому пізніше.