6.4: Основні статистичні поняття та методи

У цьому розділі та наступному мета полягає в тому, щоб зрозуміти, аналізувати та критикувати аргументи за допомогою статистики. Такі аргументи надзвичайно поширені; вони також часто маніпулятивні та/або помилкові. Як одного разу сказав Марк Твен: «Існує три види брехні: брехня, проклята брехня та статистика». Однак можна при мінімальному розумінні деяких основних статистичних понять та прийомів, поряд з усвідомленням різних способів, якими вони зазвичай зловживаються (навмисно чи ні), побачити «брехню» за те, що вони є: погані аргументи, які не повинні переконувати нас. У цьому розділі ми надамо основу базових статистичних знань. У наступному ми розглянемо різні статистичні помилки.

Середні значення: середнє проти медіани

Слово «середнє» слизьке: воно може використовуватися для позначення як до середнього арифметичного, так і до медіани набору значень. Середнє і медіана часто різні, і коли це так, використання слова «середнє» є двозначним. Розумна людина може використовувати цей факт в свою риторичну користь. Ми чуємо слово «середній», кинуте зовсім небагато в аргументах: середньостатистична сім'я має такий-такий дохід, середній студент несе такий-небудь в студентському кредиті борг і так далі. Аудиторія повинна сприймати цю вигадану середню сутність як представник усіх інших, і залежно від висновку, в якому вона намагається переконати людей, людина, яка робить аргумент, буде вибирати між середнім і медіанним, вибираючи число, яке найкраще відповідає її риторичній меті. Тому важливо, щоб критичний слухач запитував кожного разу, коли використовується слово «середнє», «Це стосується середнього чи медіани? Яка різниця між ними? Як би використання іншого вплине на аргумент?»

Простий приклад може зробити це зрозумілим. (Натхнення для цього прикладу, як і багато чого, що випливає, походить від Даррелла Хаффа, 1954, Як брехати зі статистикою, Нью-Йорк: Нортон.) Я керую бізнесом з укладання укладання на стороні - логічні конструкції (дочірня компанія Logicorp, що повністю належить). У тому числі і я, 22 людини працюють в «Логічних конструкціях». Ось скільки вони платять на рік: 350 000 доларів для мене (я начальник); 75 000 доларів кожен для двох бригадирів; 70 000 доларів для мого бухгалтера; 50 000 доларів за п'ять каменярів; 30 000 доларів для офісного секретаря; 25 000 доларів для двох учнів; і 20 000 доларів для десяти робітників. Щоб розрахувати середню зарплату в Logical Constructions, складаємо всі індивідуальні зарплати (мої 350 000 доларів, 75 000 доларів двічі, оскільки є два бригадири, і так далі) і ділимо на кількість працівників. Результат - 50 000 доларів. Щоб розрахувати середню заробітну плату, ми ставимо всі індивідуальні зарплати в числовому порядку (десять записів у розмірі 20 000 доларів для робітників, потім два записи по 25 000 доларів для учнів тощо) і знаходимо середнє число - або, як у випадку з нашим набором, який має парну кількість записів, середнє значення двох середніх цифри. Середні два числа обидва $25,000, так що медіана зарплата $25,000.

Ви, можливо, помітили, що багато моїх працівників не платять особливо добре. Зокрема, ті, що знаходяться внизу - мої десять робітників - дійсно отримують вал: 20 000 доларів на рік для такого роду нерозривних робіт - це сира угода. Припустимо, одного разу, коли я проїжджаю повз нашого будівельного майданчика (в задній частині мого лімузина, природно), я помічаю, що деякі зовнішні агітатори співпрацювали з моїми робітниками під час їх (10-хвилинна) обідня перерва - ви знаєте тип, організатори профспілки, пінко коміки (в цій історії, я жадібний капіталіст; грати разом). Вони намагаються переконати моїх співробітників торгуватися колективно за вищу заробітну плату. Зараз у нас дискусія: чи потрібно платити працівникам логічних конструкцій більше? Я беру одну сторону питання; працівники та організатори беруть іншу. Під час складання наших аргументів ми могли б обоє посилатися на середнього працівника в логічних конструкціях. Я хочу зробити це таким чином, щоб здавалося, що цей міфічний працівник працює досить добре, і тому нам не потрібно нічого змінювати; організатори захочуть зробити це таким чином, що робить здається, що середній працівник взагалі не дуже добре. У нас є два почуття «середнього» на вибір: середнє та середнє. У цьому випадку середнє значення вище, тому я буду використовувати його: «Середній працівник логічних конструкцій складає 50 000 доларів на рік. Це досить хороша заробітна плата!» Мої опоненти, організатори профспілки, будуть протистояти, використовуючи медіану: «Середній працівник логічних конструкцій робить лише $25,000 на рік. Спробуйте виховати сім'ю на таку безцінь!»

Багато що висить, яке почуття «середнього» ми вибираємо. Це вірно в багатьох реальних життєвих обставин. Наприклад, дохід домогосподарств у Сполучених Штатах розподіляється так само, як зарплати в моїй вигаданій компанії Logical Constructions: ті, хто знаходиться у верхній частині діапазону, набагато краще, ніж ті, що знаходяться внизу. (У 2014 році найбагатша п'ята частина американських домогосподарств становила понад 51% доходу; найбідніша п'ята - 3%.) За таких обставин середнє значення вище медіани. У 2014 році середній дохід домогосподарств у США становив $72 641. Це досить добре! Медіана, однак, становила лише 53 657 доларів. Це велика різниця! «Середня сім'я робить близько 72,000 доларів на рік» звучить набагато краще, ніж «Середня сім'я робить близько 53 000 доларів на рік».

Нормальні розподіли: стандартне відхилення, довірчі інтервали

Якщо ви дали IQ тести цілій купі людей, а потім графіки результати на гістограмі або барній діаграмі - так що кожен раз, коли ви бачили конкретний бал, планка для цього рахунку буде отримати вище - ви б в кінцевому підсумку з такою картинкою:

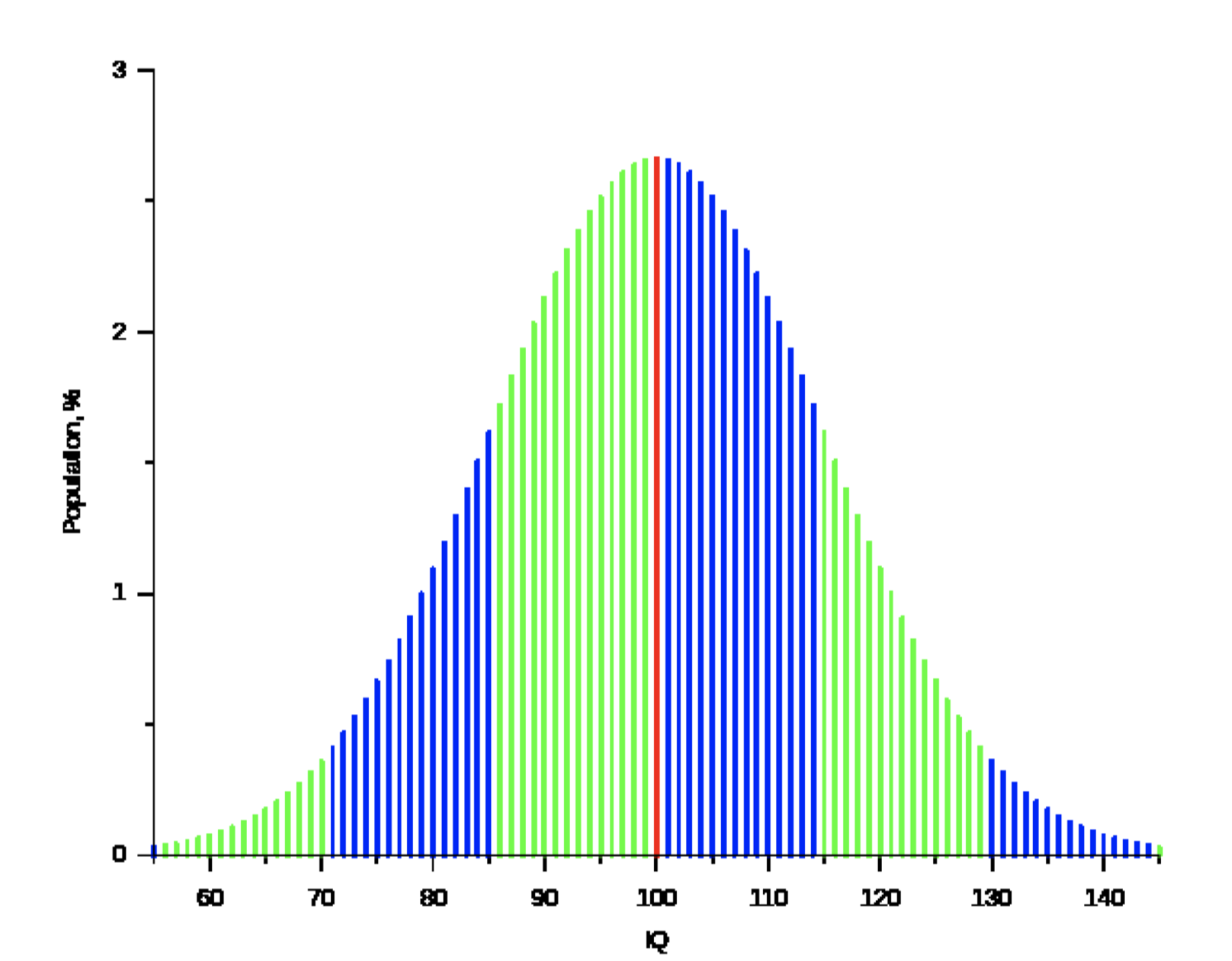
Такий вид розподілу називають «нормальним» або «гауссовим» розподілом (Гауссовим», тому що великий німецький математик Карл Фрідріх Гаусс вивчив такі розподіли на початку 19 століття (у зв'язку з їх співвідношенням до похибок вимірювання).); через свою форму його часто називають «крива дзвінка». Крім IQ, багато явищ в природі (приблизно) розподілені нормально: висота, артеріальний тиск, рухи окремих молекул у колекції, тривалість життя промислових продуктів, похибки вимірювань тощо. (Це наслідок математичного результату, Центральна гранична теорема, основний результат якої полягає в тому, що якщо якась випадкова величина (така риса, як IQ, наприклад, бути конкретним) є сумою багатьох незалежних випадкових величин (причини відмінностей IQ: багато різних генетичних факторів, багато різних фактори навколишнього середовища), тоді змінна (IQ) буде нормально розподілена. Математична теорема стосується абстрактних чисел, а розподіл є лише ідеально «нормальним», коли кількість незалежних змінних наближається до нескінченності. Ось чому реальні дистрибутиви є лише приблизно нормальними.) І навіть коли риси зазвичай не розподілені, може бути корисно ставитися до них так, ніби вони були. Це пов'язано з тим, що крива дзвінка забезпечує надзвичайно зручну відправну точку для здійснення певних висновків. Це зручно тим, що про таку криву можна знати все, вказавши дві її ознаки: її середнє (яке, оскільки крива симетрична, таке ж, як її медіана) і стандартне відхилення.

Ми вже розуміємо середнє значення. Давайте візьмемося за стандартне відхилення. Нам не потрібно вчитися його обчислювати (хоча це можна зробити); ми просто хочемо якісного (на відміну від кількісного) розуміння того, що це означає. Грубо кажучи, це міра поширення даних, представлених на кривій; це спосіб вказати, наскільки, в середньому, значення, як правило, відхиляються від середнього. Приклад може зробити це зрозумілим. Розглянемо два міста: Мілуокі, Вісконсин і Сан-Дієго, Каліфорнія. Ці два міста відрізняються різними способами, не в останню чергу погодою, яку відчувають їхні жителі. Відклавши опади, давайте зосередимося саме на температурі. Якщо ви записували високі температури щодня в кожному місті протягом тривалого періоду часу і зробили гістограму для кожного (з температурою на осі x, кількістю днів на осі y), ви отримаєте дві дуже різні криві. Може бути, щось на зразок цього:

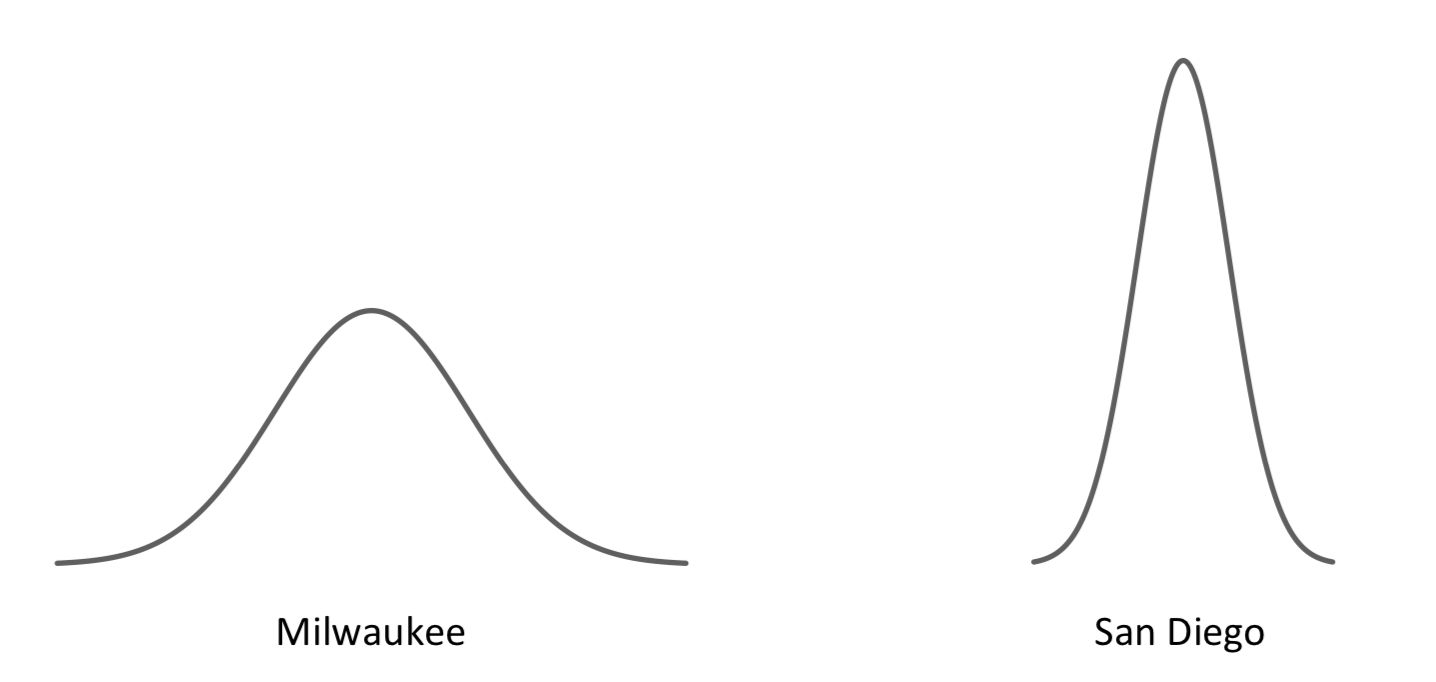
Середні високі температури для двох міст - вершини кривих - звичайно, були б різними: Сан-Дієго в середньому тепліше, ніж Мілуокі. Але діапазон температур, що спостерігаються в Мілуокі, набагато більший, ніж у Сан-Дієго: деякі дні в Мілуокі висока температура нижче нуля, тоді як в деякі дні влітку вона перевищує 100° F Сан-Дієго, з іншого боку, в основному завжди ідеальний: близько 70° або близько того . (Це, звичайно, перебільшення, але не багато одного. Середній максимум у Сан-Дієго в січні становить 65°; у липні - 75°. Тим часом у Мілуокі середній максимум у січні становить 29°, тоді як у липні - 80°.) Стандартне відхилення температур в Мілуокі набагато більше, ніж в Сан-Дієго. Це відбивається на формах відповідних кривих дзвонів: Мілуокі коротший і ширший - з нетривіальною кількістю днів при екстремальних температурах і широким поширенням протягом усіх інших днів - і Сан-Дієго вище і вужче - з температурою, що коливається в жорсткому діапазоні цілий рік, а отже, і більше днів на кожна температура реєструється (що пояснює відносні висоти кривих).

Як тільки ми дізнаємося середнє і стандартне відхилення нормального розподілу, ми знаємо все, що нам потрібно знати про це. Є три дуже корисних факту про ці криві, які можуть бути викладені з точки зору середнього і стандартного відхилення (SD). Що стосується математичного факту, 68,3% населення, зображеного на кривій (будь то люди з певними IQ, дні, коли були досягнуті певні температури, вимірювання з певною кількістю похибки) потрапляє в діапазон одного стандартного відхилення по обидва боки середнього. Так, наприклад, середній IQ дорівнює 100; стандартне відхилення - 15. Звідси випливає, що 68,3% людей мають IQ між 85 і 115—15 балами (один SD) по обидва боки 100 (середнє значення). Ще один факт: 95,4% населення, зображеного на кривій дзвінка, потраплять в діапазон двох стандартних відхилень від середнього. Таким чином, 95,4% людей мають IQ між 70 і 130-30 балами (2 SDs) по обидва боки 100. Нарешті, 99,7% населення потрапляє в межах трьох стандартних відхилень від середнього; 99,7% людей мають IQ між 55 і 145. Ці діапазони називаються довірчими інтервалами. (Виберіть людину навмання. Наскільки ви впевнені, що вони мають IQ між 70 і 130? 95.4%, ось наскільки впевнено.) Вони є зручними орієнтирами, які зазвичай використовуються в статистичному висновку. (Власне кажучи, в сучасній практиці частіше використовуються інші довірчі інтервали: 90%, (рівно) 95%, 99% і т.д. ці діапазони лежать по обидва боки від середнього в межах нецілого числа кратних стандартного відхилення. Наприклад, рівно -95% інтервал становить 1,96 SDs в обидві сторони від середнього. Зручність калькуляторів та електронних таблиць робити нашу математику для нас робить ці довірчі інтервали більш практичними. Але ми будемо дотримуватися інтервалів 68.3/95.4/99.7 заради простоти.)

Статистичний висновок: тестування гіпотез

Якщо ми почнемо зі знання властивостей даного нормального розподілу, ми можемо перевірити претензії щодо світу, до якого ця інформація має відношення. Починаючи з кривої дзвоника—інформації загального характеру—ми можемо зробити висновки про конкретні гіпотези. Це висновки індуктивних аргументів; вони не певні, але більш-менш ймовірні. Коли ми використовуємо знання про нормальні розподіли, щоб намалювати їх, ми можемо бути точними про те, наскільки вони ймовірні. Це індуктивна логіка.

Основна закономірність видів висновків, про які ми говоримо, полягає в наступному: формулює гіпотезу, потім запускає експеримент, щоб перевірити її; тест передбачає порівняння результатів цього експерименту з тим, що відомо (деякий нормальний розподіл); залежно від того, наскільки добре результати експерименту поєднуються з тим, що очікувалося б, враховуючи фонові знання, представлені кривою дзвінка, ми робимо висновок про те, чи є гіпотеза істинною чи ні.

Хоча вони застосовні в дуже широкому діапазоні контекстів, це, мабуть, найпростіше пояснити закономірності міркування, які ми збираємося вивчити, використовуючи приклади з медицини. Такі випадки є яскравими; вони допомагають зрозуміти, роблячи наслідки потенційних помилок більш реальними. Крім того, у цих випадках гіпотези, що перевіряються, відносно прості: твердження про здоров'я людей - чи здорові вони чи хворі, чи мають вони певний стан чи ні - на відміну від гіпотез, що стосуються більших груп населення та вимірювання їх властивостей. Вивчення цих простіших випадків дозволить нам чіткіше побачити основні закономірності міркувань, які охоплюють усі такі випадки тестування гіпотез, та ознайомитись із словниковим запасом, який статисти використовують у своїй роботі.

Знання, з яких ми починаємо, - це те, як якась риса, що стосується конкретного стану, розподіляється в популяції загалом - крива дзвінка. (Знову ж таки, фактичний розподіл може бути не нормальним, але ми будемо вважати, що це в наших прикладах. Основні закономірності міркування схожі при роботі з різними видами розподілів.) Експеримент, який ми проводимо, полягає в тому, щоб виміряти відповідну рису людини, здоров'я якої ми оцінюємо. Результат порівняння з результатом цього вимірювання та відомим розподілом ознаки говорить нам щось про те, здорова людина чи ні. Припустимо, почнемо з інформації про те, як розподіляється риса серед здорових людей. Гематокрит, наприклад, є мірою того, скільки крові людини забирається еритроцитами - виражена у відсотках (від загального обсягу крові). Зниження рівня гематокриту пов'язано з анемією; більш високі рівні пов'язані з зневодненням, певними видами пухлин та іншими порушеннями. Серед здорових чоловіків середній рівень гематокриту становить 47%, при стандартному відхиленні 3,5%. Ми можемо намалювати криву, зазначивши межі довірчих інтервалів:

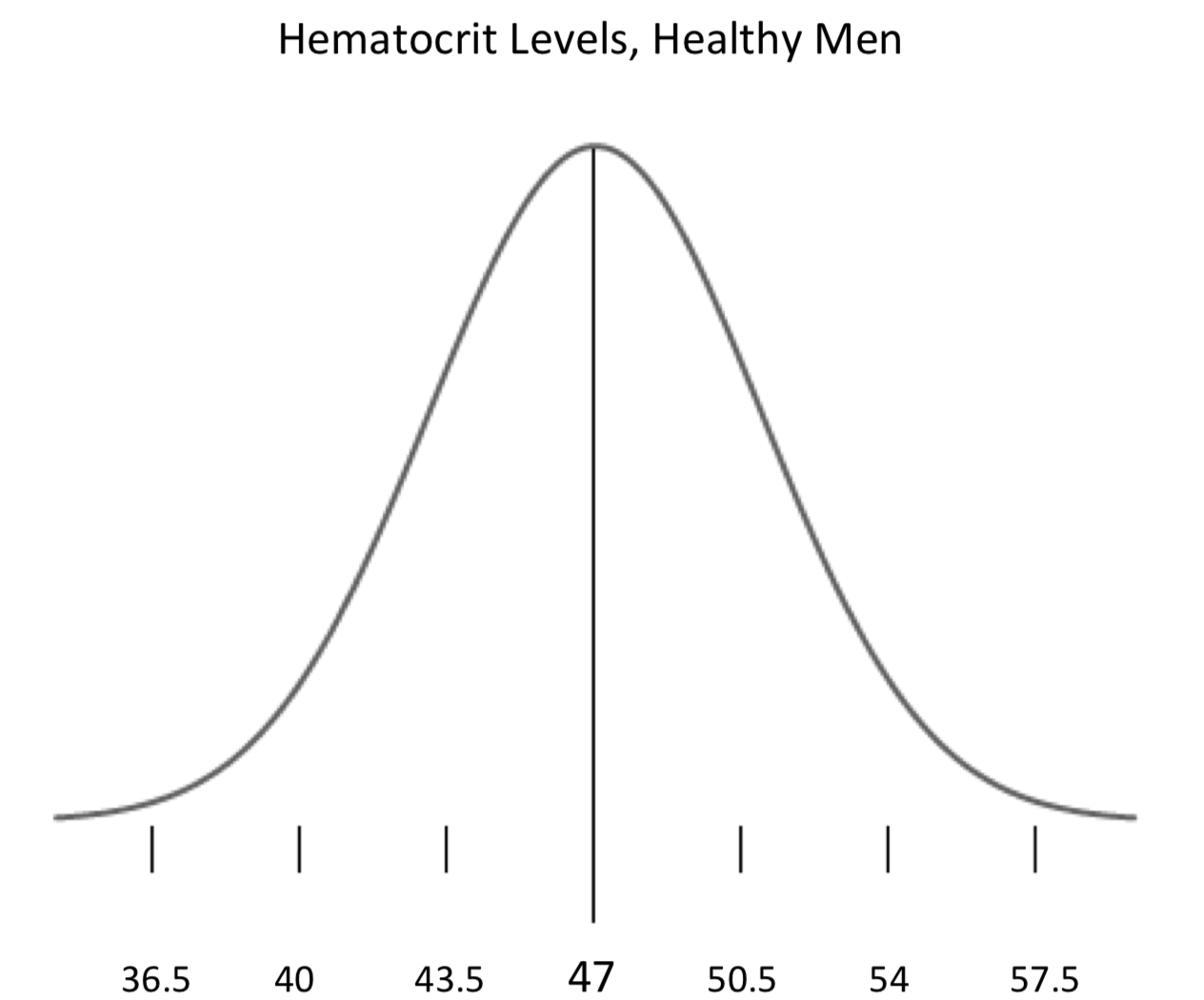
Через фіксовані математичні властивості кривої дзвінка ми знаємо, що 68,3% здорових чоловіків мають рівень гематокриту від 43,5% до 50,5%; 95,4% з них - від 40% до 54%; і 99,7% з них - від 36,5% до 57,5%. Розглянемо чоловіка, здоров'я якого ми зацікавлені в оцінці. Називайте його Ларрі. Беремо зразок крові Ларрі і вимірюємо рівень гематокриту. Ми порівнюємо його зі значеннями на кривій, щоб побачити, чи можуть бути якісь підстави турбуватися про здоров'я Ларрі. Пам'ятайте, крива говорить нам про рівень гематокриту для здорових чоловіків; ми хочемо знати, чи є Ларрі одним з них. Гіпотеза, яку ми перевіряємо, полягає в тому, що Ларрі здоровий. Статисти часто називають досліджувану гіпотезу в таких тестах як «нульова гіпотеза» - припущення за замовчуванням, те, що ми схильні вірити, якщо не виявимо доказів проти цього. У будь-якому випадку, ми вимірюємо гематокрит Ларрі; на який результат він повинен сподіватися? Зрозуміло, що він хотів би бути якомога ближче до середньої, жирної частини кривої; саме там знаходиться більшість здорових людей. Чим далі від середньостатистичного здорового рівня гематокриту він збивається, тим більше турбується про своє здоров'я. Ось як працюють ці тести: якщо результат експерименту (вимірювання гематокриту Ларрі) досить близький до середнього, у нас немає підстав відкидати нульову гіпотезу (що Ларрі здоровий); якщо результат далеко, у нас є підстави відхилити його.

Наскільки далеко від середнього знаходиться занадто далеко? Це залежить. Типовим відсіченням є два стандартних відхилення від середнього - 95,4% довірчого інтервалу. (Власне, типовий рівень зараз дорівнює рівно 95%, або 1,96 стандартних відхилень від середнього. Відтепер ми просто будемо робити вигляд, що рівні 95.4% і 95% - це одне і те ж.) Тобто, якщо рівень гематокриту Ларрі нижче 40% або вище 54%, то ми можемо сказати, що у нас є підстави сумніватися в нульовій гіпотезі про те, що Ларрі здоровий. Мовні статистики використовують для такого результату - скажімо, наприклад, якщо гематокрит Ларрі прийшов на 38% - це сказати, що це «статистично значущий». Крім того, вони вказують рівень, на якому він важливий - вказівка на відсічення інтервалу довіри, яке було використано. У цьому випадку ми б сказали, що результат Ларрі 38% є статистично значущим на рівні .05. (95% = .95; 1 - .95 = .05) Або Ларрі нездоровий (анемія, швидше за все), або він серед (приблизно) 5% здорових людей, які потрапляють за межі двох стандартних відхилень. Якби він прийшов на рівні ще далі від середнього - скажімо, 36% - ми б сказали, що цей результат є значним на рівні .003 (99,7% = .997; 1 - .997 = .003). Це дало б нам ще більше підстав сумніватися, що Ларрі здоровий.

Отже, коли ми розробляємо медичний тест, як це, найважливіше рішення, яке потрібно прийняти, - це те, де встановити відсічення. Знову ж таки, як правило, це 95% довіри інтервал. Якщо результат виходить за межі цього діапазону, людина перевіряє «позитивний» для будь-якого стану, за яким ми шукаємо. (Звичайно, «позитивний» результат навряд чи є позитивною новиною - у сенсі того, що ви хочете почути.) Але такі результати не є переконливими: можливо, нульова гіпотеза (ця людина здорова) є правдою, і що вони просто одні з відносних рідкісних 5%, які падають на околиці кривої. У такому випадку ми б сказали, що тест дав людині «хибнопозитивний» результат: тест вказує на хворобу, коли насправді її немає. Статистики називають такого роду помилку «помилкою типу I». Ми могли б зменшити кількість помилкових результатів, які дає наш тест, змінивши рівень довіри, при якому ми даємо позитивний результат. Повертаючись до конкретного прикладу вище: припустимо, що у Ларрі рівень гематокриту 38%, але він насправді не анемічний; оскільки 38% знаходиться за межами двох діапазонів стандартних відхилень, наш тест дав би Ларрі хибнопозитивний результат, якби ми використовували рівень довіри 95%. Однак, якби ми підняли поріг статистичної значущості до трьох стандартних відхилень рівня 99,7%, Ларрі не отримав би позначку на анемію; не було б помилкового позитиву, помилки типу I.

Тому ми завжди повинні використовувати ширший діапазон на таких видах тестів, щоб уникнути помилкових спрацьовувань, чи не так? Не так швидко. Існує ще одна помилка, яку ми можемо зробити: помилкові негативи, або помилки типу II. Збільшення нашого асортименту збільшує наш ризик цього другого виду фол-Ап. Внизу там на худому кінці кривої є відносно мало здорових людей. Хворі люди - це ті, хто, як правило, має вимірювання в цьому діапазоні; це ті, кого ми намагаємося зловити. Коли ми видаємо помилковий негатив, ми пропускаємо їх. Помилковий негатив виникає, коли тест говорить вам, що немає підстав сумніватися в нульовій гіпотезі (що ви здорові), коли насправді ви хворі. Якщо ми збільшимо наш діапазон від двох до трьох стандартних відхилень - від рівня 95% до рівня 99,7% - ми уникнемо давати хибнопозитивний результат Ларрі, який здоровий, незважаючи на низький рівень гематокриту 38%. Але ми в кінцевому підсумку дамо помилкові запевнення деяким анемічним людям, які мають рівні, подібні до Ларрі; той, хто має рівень 38% і хворий, отримає помилково негативний результат, якщо ми позначимо лише тих, хто знаходиться поза інтервалом довіри 99,7% (36,5% - 57,5%).

Це багаторічна дилема в медичному скринінгу: як найкраще досягти балансу між двома типами помилок - між непотрібними тривожними здоровими людьми з хибнопозитивними результатами та нездатністю виявити хворобу у людей з помилковими негативними результатами. Терміни клініцисти використовують для характеристики того, наскільки добре діагностичні тести виконують за цими двома вимірами чутливість та специфічність. Високочутливий тест вловить велику кількість випадків хвороби - він має високий рівень справжніх позитивних результатів; звичайно, це відбувається ціною збільшення кількості хибнопозитивних результатів, а також. Тест з високим рівнем специфічності матиме високий рівень справжніх негативних результатів - правильне визначення здорових людей як таких; однак вартість підвищеної специфічності є збільшенням кількості помилково негативних результатів - хворих людей, яких тест пропускає. Оскільки кожен помилковий позитив - це втрачена можливість для справжнього негативу, підвищення чутливості відбувається ціною зниження специфічності. І оскільки кожен помилковий негатив є пропущеним істинним позитивом, збільшення специфічності відбувається ціною зменшення специфічності. Останній біт медичного жаргону: скринінговий тест є точним до того ступеня, що він є одночасно чутливим і специфічним.

Враховуючи достатньо ретельну інформацію про розподіл ознак серед здорових та хворих груп населення, клініцисти можуть налаштувати свої діагностичні тести настільки чутливими або специфічними, наскільки їм подобається. Але оскільки ці дві властивості тягнуть в протилежних напрямках, існують межі ступеня точності, яка можлива. І в залежності від конкретного випадку може бути бажано пожертвувати специфікою для більшої чутливості, або навпаки.

Щоб побачити, як скринінговий тест може бути сфальсифікований, щоб максимізувати чутливість, давайте розглянемо абстрактний гіпотетичний приклад. Припустимо, ми знали розподіл певної ознаки серед населення людей, які страждають певним захворюванням. (Протиставте це з нашою відправною точкою вище: знання про розподіл серед здорових людей.) Цей вид знань є поширеним у медичному контексті: різні так звані біомаркери - генні мутації, білки в крові тощо, як відомо, свідчать про певні умови; часто можна знати, як такі маркери розподіляються між людьми з цим станом. Знову ж таки, зберігаючи його абстрактним та гіпотетичним, припустимо, ми знаємо, що серед людей, які страждають на хворобу X, середній рівень певного біомаркера β для захворювання становить 20, зі стандартним відхиленням 3. Ми можемо підсумувати ці знання за допомогою кривої:

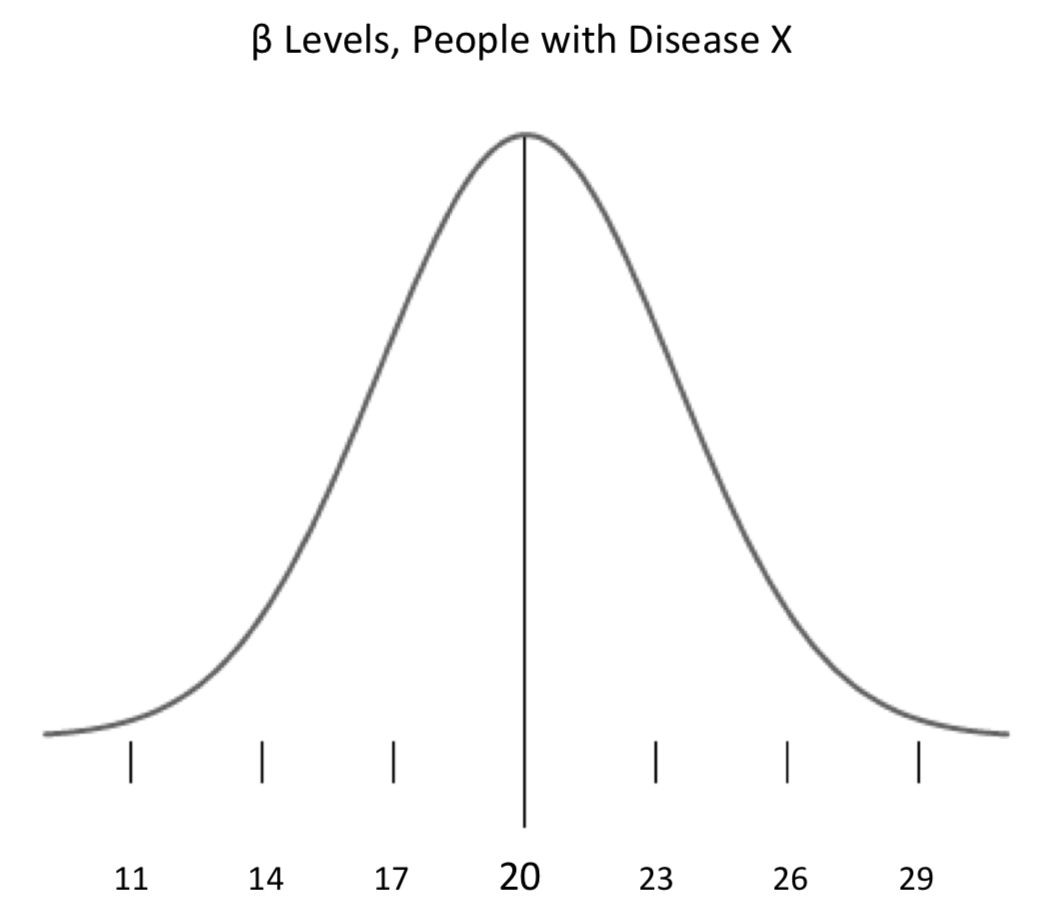
Тепер, припустимо, хвороба X дійсно дуже серйозна. Було б корисним для громадського здоров'я, якби ми змогли розробити скринінговий тест, який міг би вловити якомога більше випадків - тест з високою чутливістю. Враховуючи знання, які ми маємо про розподіл β серед пацієнтів із захворюванням, ми можемо зробити наш тест таким чутливим, наскільки нам подобається. Ми знаємо, як математичний факт, що 68,3% людей з хворобою мають β-рівні між 17 і 23; 95,4% людей з хворобою мають рівні між 14 і 26; 99,7% мають рівні між 11 і 29. Враховуючи ці факти, ми можемо розробити тест, який вловить 99,7% випадків хвороби X так: виміряйте рівень біомаркера β у людей, і якщо вони мають значення між 11 і 29, вони отримують позитивний результат тесту; позитивний результат свідчить про захворювання. Це вловить 99,7% випадків стану, оскільки обраний діапазон - це три стандартні відхилення по обидві сторони від середнього, і цей діапазон містить 99,7% нездорових людей; якщо ми позначимо всіх у цьому діапазоні, ми зловимо 99,7% випадків. Звичайно, ми, ймовірно, в кінцевому підсумку зловити багато здорових людей, а також, якщо ми кидаємо нашу мережу так широко; ми отримаємо багато помилкових спрацьовувань. Ми могли б виправити це, зробивши наш тест менш чутливим, скажімо, знизивши поріг для позитивного тесту до двох діапазонів стандартних відхилень 14 - 26. Зараз ми б зловили лише 95,4% випадків хвороби, але зменшили б кількість здорових людей, які отримували помилкові спрацьовування; натомість вони отримали б справжні негативні результати, підвищуючи специфічність нашого тесту.

Зверніть увагу, що спосіб, який ми використовували криву дзвінка в нашому гіпотетичному тесті на хворобу X, відрізнявся від того, як ми використовували криву дзвінка в нашому тесті рівня гематокриту вище. У цьому випадку ми позначали людей як потенційно хворих, коли вони потрапляли за межі діапазону навколо середнього; у новому випадку ми позначали людей як потенційно хворих, коли вони потрапляли в певний діапазон. Ця різниця відповідає відмінностям у двох популяціях, які представляють відповідні розподіли: у випадку гематокриту ми почали з кривої, що зображує розподіл ознаки серед здорових людей; у другому випадку ми почали з кривої, яка розповідає нам про хворих людей. У першому випадку хворі люди будуть, як правило, далекі від середнього; в останньому вони, як правило, скупчуються ближче.

Напруженість, яку ми відзначили між чутливістю та специфічністю - між збільшенням кількості випадків, які виявляє наш діагностичний тест, і зменшенням кількості помилкових спрацьовувань, які він виробляє, можна побачити, коли показують криві для здорових груп населення та хворих груп населення на одному графіку. У сироватці крові вагітних є біомаркер під назвою альфа-фетопротеїн. Низький рівень цього білка пов'язаний з синдромом Дауна у плода; високі рівні пов'язані з дефектами нервової трубки, такими як відкритий spina bifida (хребет не повністю всередині тіла) та аненцефалія (навряд чи розвивається будь-який з мозків/черепа). Це серйозні стани - особливо ті, що пов'язані з високим рівнем: якщо у дитини відкрита біфіда хребта, потрібно бути готовим до цього (з фахівцями та спеціальним обладнанням) під час народження; у випадках аненцефалії плід не буде життєздатним (в гіршому випадку) або буде жити без відчуттів або обізнаність (в кращому випадку?). На ранніх термівах вагітності ці стани обстежуються. Оскільки вони настільки серйозні, ви хотіли б зловити якомога більше випадків. І все ж, ви хотіли б уникнути тривожних помилкових позитивних результатів для цих умов. Наступна діаграма, з кривими дзвінка для здорових немовлят, тих, у кого відкрита біфіда хребта та аненцефалія, ілюструє складні компроміси у прийнятті таких рішень (Зображення з публікації на www.pregnancylab.net Девід Гренаш, доктор філософії: http://www.pregnancylab.net/2012/11/...e-defects.html):

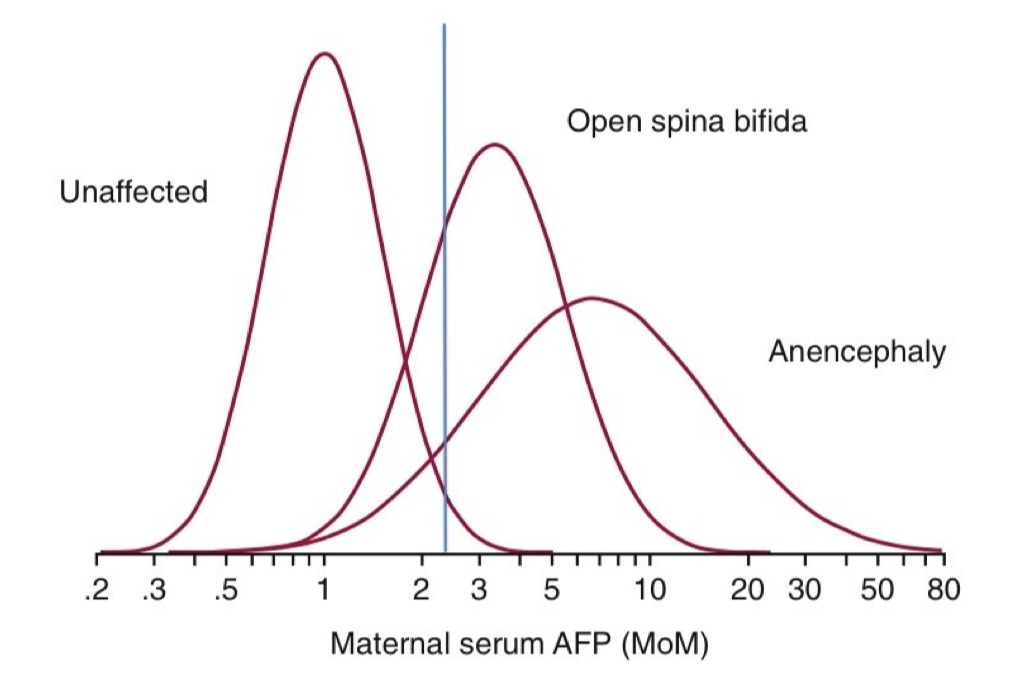
Вертикальна лінія на 2,5 мОм (кратні медіані) є типовим відсіченням для «позитивного» результату (позначено для потенційних задач). З одного боку, є значні частини двох кривих, що представляють нездорове населення - зліва від цієї лінії - які не будуть позначені тестом. Це випадки хвороби, які ми не зловитимемо - помилкові негативи. З іншого боку, є багато здорових немовлят, батьки яких будуть надмірно насторожені. Площа кривої «незмінної» праворуч від лінії може виглядати не так багато, але ці криві не намальовані в лінійному масштабі. Якби вони були, ця крива була б багато (багато!) вище, ніж два для відкритої біфіди хребта та аненцефалії: ці умови справді рідкісні; є набагато більше здорових дітей. Підсумок полягає в тому, що крихітна частина здорової кривої представляє багато помилкових спрацьовувань.

Знову ж таки, такий компроміс між чутливістю та специфічністю часто представляє клініцистам складний вибір при розробці діагностичних тестів. Вони повинні зважити переваги лову якомога більше випадків проти потенційних витрат занадто багато помилкових спрацьовувань. Серед витрат - психологічні наслідки отримання помилкового позитиву. Як батько, який пережив це, я можу сказати вам, що отримання новин про потенційну відкриту біфіду хребта або аненцефалію є досить травматичним. (Хибнопозитивний: малюк був абсолютно здоровий.) Але може бути і гірше. Наприклад, коли біомаркер СНІДу був вперше виявлений в середині 1980-х років, люди Центрів контролю захворювань розглядали скринінг на захворювання серед усього населення. Тест був чутливим, тому вони знали, що вловить багато випадків. Але вони також знали, що буде велика кількість помилкових спрацьовувань. Враховуючи істерію, яка, ймовірно, виникне внаслідок такої кількості діагнозів страшної хвороби (в ті часи люди майже нічого не знали про СНІД; люди вмирали від таємничої хвороби, а страх і дезінформація були широко поширені), вони вирішили проти загального скринінгу. Іноді до негативних наслідків помилкових спрацьовувань відносять фінансові та медичні витрати. У 2015 році Американське онкологічне товариство змінило свої рекомендації щодо скринінгу на рак молочної залози: замість того, щоб починати щорічну мамографію у віці 40 років, жінкам слід чекати до 45 років. (За винятком тих, хто, як відомо, знаходиться в групі ризику, хто повинен почати раніше.) Це було спірне рішення. Після цього багато жінок прийшли свідчити, що їхнє життя було врятовано раннім виявленням раку молочної залози, і що згідно з новими рекомендаціями вони, можливо, не так добре впоралися. Але проти вигоди від лову цих випадків САУ довелося зважувати витрати на хибно-позитивні мамограми. Спостереження за позитивною мамографією часто є біопсією; це інвазивна хірургічна процедура і дорога. Контраст, що з подальшим позитивним результатом для відкритої біфіди/аненцефалії хребта: неінвазивне, дешеве ультразвукове дослідження. І на відміну від УЗД, біопсію іноді досить важко інтерпретувати; ви отримуєте деякі діагнози раку, коли раку немає. Ці жінки можуть продовжувати отримувати лікування - хіміотерапію, радіацію - від раку, якого у них немає. Витрати і фізичні побічні ефекти, які є серйозними. (Особливо збочені випадки, коли саме променеве лікування викликає рак у пацієнта, якому не потрібно було лікувати для початку.) В одному дослідженні було визначено, що за кожне життя, врятоване мамографічним скринінгом, було 100 жінок, які отримали помилкові спрацьовування (і дізналися про це після біопсії) і п'ять жінок, які лікувалися від раку, у них не було. (PC Gøtzsche and KJ Jørgensen, 2013, Кокранівська база даних систематичних оглядів (6), CD001877.pub5)

Логіка тестування статистичних гіпотез відносно зрозуміла. Що не зрозуміло, так це те, як ми повинні застосовувати ці відносно прості методи в реальній практиці. Це часто пов'язане з важкими фінансовими, медичними та моральними рішеннями.

Статистичний висновок: вибірка

Коли ми перевіряли гіпотези, нашою відправною точкою були знання про те, як риси були розподілені серед великого населення - наприклад, рівень гематокриту серед здорових чоловіків. Ми зараз задаємо нагальне питання: як ми отримуємо такі знання? Як ми з'ясуємо, як йдуть справи з дуже великим населенням? Складність полягає в тому, що перевірити кожного члена населення зазвичай неможливо. Замість цього ми повинні зробити висновок. Цей висновок включає вибірку: замість того, щоб перевіряти кожного члена популяції, ми перевіряємо невелику частину населення - вибірку - і робимо висновок з його властивостей до властивостей цілого. Це простий індуктивний аргумент:

Вибірка має властивість X.
Тому загальна чисельність населення має властивість X.

Аргумент є індуктивним: передумова не гарантує істинності висновку; це лише робить його більш імовірним. Як і у випадку з тестуванням гіпотез, ми можемо бути точними щодо ймовірностей, що беруть участь, і наші ймовірності походять від старої доброї кривої дзвінка.

Візьмемо простий приклад. (Я заборгований за цей приклад, зокрема (і для великого фону на поданні статистичних міркувань в цілому) Джону Нортону, 1998, Як працює наука, Нью-Йорк: Макгроу-Хілл, стор. 12.14 - 12.15.) Припустимо, ми намагалися виявити відсоток чоловіків у загальній популяції; ми опитуємо 100 людей, і виявляється, що в нашій вибірці 55 чоловіків. Отже, частка чоловіків в нашій вибірці становить 0,55. Ми намагаємося зробити висновок з цієї передумови до висновку про частку чоловіків у загальному населенні. Яка ймовірність того, що частка чоловіків у загальній популяції становить 0,55? Це не зовсім питання, на яке ми хочемо відповісти в таких випадках. Швидше, ми запитуємо, яка ймовірність того, що справжня частка чоловіків у загальній популяції знаходиться в деякому діапазоні по обидва боки 0,55? Ми можемо дати точну відповідь на це питання; відповідь залежить від розміру діапазону, який ви розглядаєте, звичним чином.

Враховуючи, що частка чоловіків нашої вибірки становить 0,55, порівняно більш імовірно, що справжня частка в загальній чисельності населення близька до цього числа, рідше, що вона далеко. Наприклад, з огляду на результат нашого опитування, більш імовірно, що насправді 50% населення - це чоловіки, ніж лише 45% - чоловіки. І все ж менш імовірно, що тільки 40% - чоловіки. Та ж картина тримається і в зворотному напрямку: швидше за все, справжній відсоток чоловіків становить 60%, ніж 65%. Взагалі кажучи, чим далі від наших результатів опитування ми йдемо, тим менша ймовірність того, що ми маємо справжню цінність для загальної популяції. Випадання в описаних ймовірностях набуває вигляду кривої дзвінка:

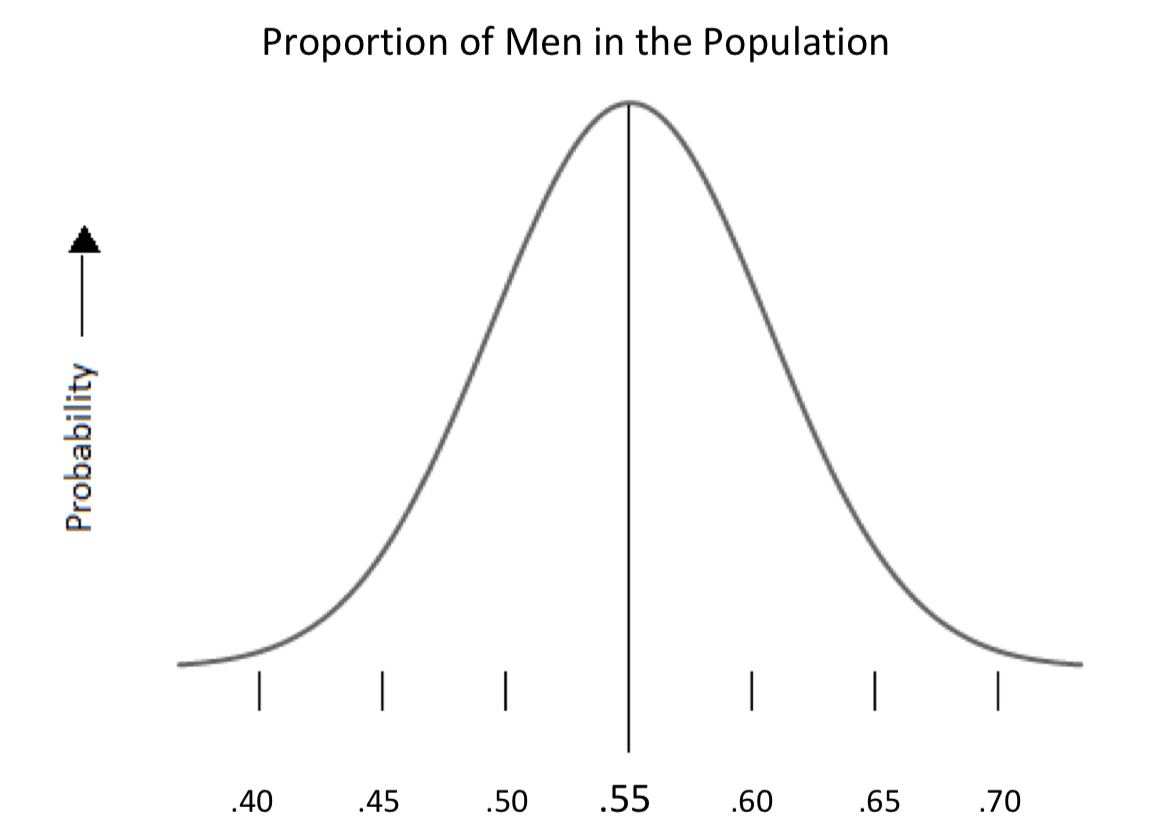
Стандартне відхилення 0,05 є функцією нашого розміру вибірки 100. (І середнє (наш результат 0,55). Математичні деталі розрахунку не повинні нас затримувати.) Ми можемо використовувати звичайні інтервали довіри - знову ж таки, з 2 стандартними відхиленнями, 95,4% - стандартною практикою - для інтерпретації результатів нашого опитування: ми впевнені - на основі 95% - що загальна чисельність населення становить від 45% до 65% чоловіків.

Це досить широкий асортимент. Наш результат не такий вражаючий (особливо з огляду на те, що ми знаємо, що реальна кількість дуже близька до 50%). Але це найкраще, що ми можемо зробити, враховуючи обмеження нашого опитування. Головним обмеженням, звичайно, був розмір нашої вибірки: 100 чоловік просто не дуже багато. Ми могли б звузити діапазон, в якому ми впевнені на 95%, якщо ми збільшимо розмір вибірки; це, ймовірно, (хоча і не звичайно) дасть нам пропорцію в нашому зразку ближче до істинного значення (приблизно) .5. Взаємозв'язок між розміром вибірки і шириною довірчих інтервалів є чисто математичним. Коли розмір вибірки зростає, стандартне відхилення знижується - крива звужується:

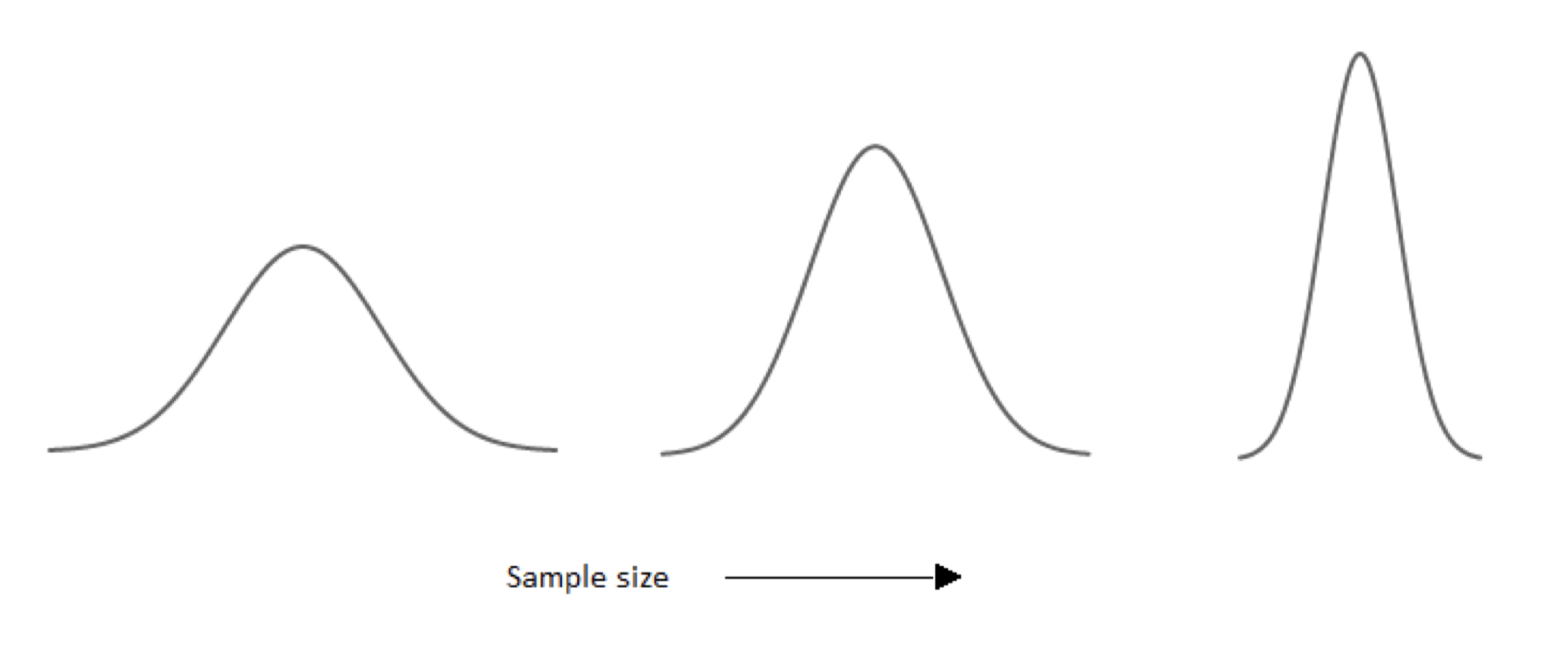
Схема міркування на дисплеї в нашому прикладі іграшок така ж, як і в цілому використовується при вибірці. Мабуть, найбільш звичними екземплярами вибірки в повсякденному житті є опитування громадської думки. Замість того, щоб намагатися визначити частку людей у загальному населенні, які є чоловіками (не справжня таємниця), опитувальники намагаються визначити частку даного населення, яке, скажімо, має намір проголосувати за певного кандидата, або схвалити роботу, яку виконує президент, або вірять в снігової людини. Опитувальники опитують вибірку людей з цього питання, і в кінцевому підсумку отримують результат: 29% американців вірять у бігфута, наприклад. (Ось фактичне опитування з таким результатом: angusreidglobal.com/wp-conten... 3.04_myths.pdf)

Але номер заголовка, як ми бачили, не розповідає про всю історію. 29% вибірки (в даному випадку близько 1000 американців) повідомили, що вірять у бігфута; це не випливає з упевненістю, що 29% загального населення (усі американці) мають таку віру. Швидше за все, опитувальники мають певний ступінь впевненості (знову ж таки, 95% є стандартним), що фактичний відсоток американців, які вірять у снігової людини, знаходиться в деякому діапазоні близько 29%. Можливо, ви чули «похибку», згадану у зв'язку з такими опитуваннями. Ця фраза відноситься до самого діапазону, про який ми говоримо. В опитуванні про снігової людини похибка становить 3%. (Насправді, це 3,1%, але не шкода.) Це відстань від середнього (29% знайдених у вибірці) і кінці двох стандартних відхилень довіри інтервалу - діапазон, в якому ми 95% впевнені, що справжнє значення лежить. Знову ж таки, цей діапазон є лише математичною функцією розміру вибірки: якщо розмір вибірки становить близько 100, похибка становить близько 10% (див. Приклад іграшки вище: 2 SDs = .10); якщо розмір вибірки становить близько 400, ви отримуєте це до 5%; при 600 ви знижуєтесь до 4%; приблизно 1,000, 3%; щоб знизити до 2%, вам потрібно близько 2500 в вибірці, і щоб отримати до 1%, вам потрібно 10000. (Цікавий математичний факт: ці відносини тримаються незалежно від того, наскільки велика загальна сукупність, з якої ви вибірки (до тих пір, поки це вище певного порогу). Це може бути розмір населення Вісконсіна або населення Китаю: якщо ваша вибірка становить 600 вісконсинітів, ваша похибка становить 4%; якщо це 600 китайців, це все ще 4%. Це контрінтуїтивно, але правда - принаймні, абстрактно. Ми опускаємо дуже серйозні труднощі, які виникають під час фактичного опитування (про які ми обговоримо): пошук правильних 600 вісконсинітів або китайців, щоб зробити ваше опитування надійним; Китай буде представляти більше труднощів, ніж Вісконсін.) Таким чином, реальний результат опитування снігової людини приблизно такий: десь від 26% до 32% американців вірять у бігфута, і ми на 95% впевнені, що це правильний діапазон; або, по-іншому, ми використали метод визначення справжньої частки американців, які вірять у бігфута, що може бути очікували визначити діапазон, в якому справжнє значення фактично падає 95% часу, а діапазон, який був результатом нашого застосування методу з цього приводу, становив 26% - 32%.

Це останнє речення, ми повинні визнати, зробило б досить паршивий заголовок газети («29% американців вірять у снігової людини!» набагато сексуальніше), але це найчесніше уявлення про те, що насправді показують результати такого роду вправи вибірки. Вибірка дає нам діапазон, який буде ширшим або вужчим залежно від розміру зразка, і навіть не гарантує, що фактичне значення знаходиться в межах цього діапазону. Це найкраще, що ми можемо зробити; це індуктивні, а не дедуктивні аргументи.

Нарешті, щодо теми вибірки ми повинні визнати, ніж у реальній практиці опитування важко. Математичні зв'язки між розміром вибірки та похибкою/впевненістю, які ми відзначили, тримаються в анотації, але реальні опитування можуть мати помилки, які виходять за рамки цих теоретичних обмежень щодо їх точності. Оскільки президентські вибори в США 2016 року - і так зване голосування «Brexit» у Сполученому Королівстві того ж року, і багато, багато інших прикладів протягом історії опитування громадської думки - показали нам, опитування можуть систематично помилятися. Види фактів, про які ми заявляли - що при розмірі вибірки 600 опитування має похибку 4% на рівні довіри 95% - тримаються лише на припущенні, що існує систематичний зв'язок між вибіркою та загальною сукупністю, яку він повинен представляти; а саме, що вибірка є представник. Репрезентативна вибірка відображає загальну чисельність населення; у випадку людей це означає, що вибірка та загальна чисельність населення мають однаковий демографічний склад - однаковий відсоток старих та молодих людей, білих людей та кольорових людей, багатих людей та бідних людей тощо тощо Опитування, зразки яких є не представник, швидше за все, спотворює особливість населення, яке вони намагаються захопити. Припустимо, я хотів дізнатися, який відсоток населення США прихильно ставиться до Дональда Трампа. Якби я запитав 1000 людей, скажімо, в сільській місцевості Оклахоми, я б отримав один результат; якби я запитав 1000 людей у центрі Манхеттена, я б отримав набагато інший результат. Жодна з цих двох зразків не є репрезентативною для населення Сполучених Штатів в цілому. Щоб отримати такий зразок, мені довелося б бути набагато обережніше, кого я опитував. Відомий приклад з історії публічних опитувань досить яскраво ілюструє труднощі тут: на президентських виборах в США 1936 року претендентами були республіканець Альф Лендон з Канзасу, і чинний президент Франклін Рузвельт. (нині неіснуючий) журнал «Літературний дайджест» провів опитування з 2,4 мільйонами (!) учасників, і передбачив, що Лендон переможе в зсуві. Натомість він програв у зсуві; ФДР виграла другий з чотирьох своїх президентських виборів. Що пішло не так? З таким великим розміром вибірки, похибка буде крихітною. Проблема полягала в тому, що їх вибірка не була репрезентативною для американського населення. Вони вибирали учасників випадковим чином з трьох джерел: (а) їх список абонентів; (б) форми реєстрації автомобілів; і (c) телефонні списки. Проблема цієї процедури відбору полягає в тому, що всі три групи, як правило, багатші за середні. Це був 1936 рік, під час глибини Великої депресії. Більшість людей не мали достатнього наявного доходу, щоб підписатися на журнали, не кажучи вже про наявність телефонів або власних автомобілів. Таким чином, опитування перевищило вибірку республіканських виборців і отримало перекошені результати. Навіть великий і, здавалося б, випадковий зразок може привести одного в оману. Саме це ускладнює опитування: знайти репрезентативні зразки важко. (Це навіть складніше, ніж цей абзац робить це бути. Зазвичай неможливо, щоб зразок - люди, з якими ви розмовляли по телефону про президента або про що завгодно - точно відобразити демографічні показники населення. Тож опитувальники повинні зважувати відповіді певних членів їх вибірки більше, ніж інші, щоб компенсувати ці розбіжності. Це більше мистецтво, ніж наука. Різні опитувальники, представлені з точно такими ж даними, будуть робити різні варіанти щодо того, як зважити речі, і в кінцевому підсумку повідомлять про різні результати. Дивіться цей захоплюючий шматок для прикладу: www.nytimes.com/interactive/2... про.html_r=0)

Варто відзначити й інші практичні труднощі з опитуванням. По-перше, те, як сформульовано ваше опитування питання, може мати велике значення в результатах, які ви отримуєте. Як ми обговорювали в розділі 2, обрамлення питання - слова, що використовуються для визначення певної політики чи позиції - може мати драматичний вплив на те, як відносно неінформована людина буде відчувати себе про це. Якщо ви хотіли дізнатися думку американської громадськості про те, чи є це гарна ідея оподаткувати передачу багатства спадкоємцям людей, чиї володіння перевищують $5.5 млн або близько того, ви отримаєте один набір відповідей, якщо ви назвали політику «податок на нерухомість», інший набір відповідей, якщо ви посилалися до нього як «податок на спадщину», і ще інший набір, якщо ви назвали його «податок на смерть». Опитування жителів Теннессі показало, що 85% виступали проти «Obamacare», тоді як лише 16% виступали проти «Застрахувати Теннессі» (це те ж саме, звичайно). (Джерело: http://www.nbcnews.com/politics/elec... -power-n301031) Навіть незначні зміни в формулюванні питань можуть змінити результати соціологічного опитування. Ось чому виборча фірма Gallup не змінювала формулювання свого президентського питання з 1930-х років. Вони завжди запитують: «Ви схвалюєте чи не схвалюєте те, як [ім'я президента] обробляє свою роботу на посаді президента?» Відхилення від цього стандартного формулювання може дати різні результати. Опитувальна фірма Ipsos виявила, що її опитування були більш сприятливими, ніж інші для президента. Вони простежили невідповідність різному способу формулювання свого питання, даючи додатковий варіант: «Ви схвалюєте, не схвалюєте чи маєте змішані почуття щодо того, як Барак Обама обробляє свою роботу на посаді президента?» (spotlight.ipsos-na.com/index... on-wording-on- leves-of-presidential-support/) Гіпотеза: рейтинг схвалення Обами знизиться, якщо опитувальники включили його друге ім'я (Хусейн), коли задають питання. Невеликі зміни можуть мати велике значення.

Інша складність опитування полягає в тому, що деякі питання важче отримати достовірні дані, ніж інші, просто тому, що вони включають теми, про які люди, як правило, неправдиві. Запитати когось, чи схвалює він роботу, яку робить президент, - це одне; запитати його, чи він коли-небудь обманював свої податки, скажімо, зовсім інше. Він, мабуть, не соромиться ділитися своєю думкою з першого питання; він буде набагато неохоче бути правдивим щодо останнього (припускаючи, що він коли-небудь підбивав речі у своїх податкових деклараціях). Є багато речей, які було б важко виявити з цієї причини: як часто люди ниткою, скільки вони п'ють, чи займаються вони фізичними вправами, їх сексуальні звички тощо. Іноді таке небажання ділитися правдою про себе є досить наслідковим: деякі експерти вважають, що причина опитування не спрогнозували обрання Дональда Трампа президентом США в 2016 році, полягала в тому, що деякі його прихильники були «сором'язливі» — не бажаючи визнати, що підтримували спірне. кандидат. (Дивіться тут, наприклад: https://www.washingtonpost.com/news/...=.f20212063a9c) У них не було таких сумнівів у кабінці для голосування, однак.

Нарешті, хто задає питання - і контекст, в якому його задають, може мати велике значення. Люди можуть бути більш готові відповісти на питання у відносній анонімності онлайн-опитування, трохи менше бажаючих у дещо більш особистому контексті телефонного дзвінка, і все ще менш майбутніх в інтерв'ю віч-на-віч. Опитувачі використовують усі ці методи для збору даних, і результати відповідно змінюються. Звичайно, ці фактори стають особливо актуальними, коли питання, яке опитується, є чутливим, або щось, про що люди, як правило, не чесні чи майбутні. Візьмемо приклад: найкращий спосіб виявити, як часто люди справді нитки, ймовірно, з анонімним онлайн-опитуванням. Люди, ймовірно, швидше за все, брешуть про це по телефону, і все ж, швидше за все, зроблять це в розмові віч-на-віч. Абсолютно найгіршим джерелом даних з цього питання, мабуть, було б від людей, які найчастіше його запитують: стоматологів та гігієністів. Кожен раз, коли ви заходите на прибирання, вони запитують вас, як часто ви чистите щітку і нитку; і якщо ви схожі на більшість людей, ви брешете, перебільшуючи посидючість, з якою ви відвідуєте своє стоматологічне обслуговування здоров'я («Я чищу після кожного прийому їжі і нитку двічі на день, чесно».).

Як і у випадку з тестуванням гіпотез, логіка статистичної вибірки відносно чітка. Речі стають каламутними, знову ж таки, коли прості абстрактні методи протистоять заплутаним факторам, що беруть участь у застосуванні в реальному житті.

Вправи

1. Я і купа моїх друзів готуються грати в захоплюючу гру «армійців». Разом у нас є 110 маленьких солдатиків із пластикових іграшок, яких вистачить для цілої битви. Однак деякі з нас мають більше солдатів, ніж у інших. Буде, Брайан і я кожен має 25; Роджер і Джо мають по 11; Ден має 4; Джон і Херб мають 3; Майк, Джеймі, і Денніс мають тільки 1 кожен.

(a) Яка середня кількість утримуваних армійців? Що таке медіана?
(б) Джеймі, наприклад, можливо, зрозуміло незадоволений розподілом; Я, з іншого боку, задоволений домовленістю. Захищаючи свої позиції, кожен з нас може посилатися на «середньостатистичну людину» і кількість армійців, які він має. Яке почуття «середнє» - середнє або середнє - повинен використовувати Джеймі, щоб отримати риторичну перевагу? Який сенс слід використовувати?

2. Розглянемо котів і собак—одомашненого роду, домашніх тварин (тигри не враховують). Припустимо, я зробив гістограму для дуже великої кількості домашніх кішок виходячи з їх ваги, і зробив те ж саме для домашніх собак. Який розподіл мав би більше стандартне відхилення?

3. Чоловічі висоти зазвичай розподілені, в середньому близько 70 дюймів і стандартне відхилення близько 3 дюймів. 68,3% чоловіків потрапляють в який діапазон висот? Куди падають 95,4% з них? 99,7%? Мій тесть був 76 дюймів у висоту. Який відсоток чоловіків був вищим, ніж він був?

4. Жінки, в середньому, мають нижчий рівень гематокриту, ніж у чоловіків. Середнє значення для здорових жінок становить 42%, при стандартному відхиленні 3%. Припустимо, ми хочемо перевірити нульову гіпотезу про те, що Аліса здорова. Які показання гематокриту вище яких і нижче яких результатів тесту Аліси вважався б значним на рівні .05?

5. Серед здорових людей середній (натще) рівень глюкози в крові становить 90 мг/дл, при стандартному відхиленні - 9 мг/дл. Які рівні на високому і нижньому кінці 95,4% довільного інтервалу? Нещодавно я здав аналіз крові і отримав результат 100 мг/дл. Чи є цей результат значним на рівні .05? Мій результат був позначений як потенційно свідчить про те, що я «перед діабетиком» (високий рівень глюкози в крові є маркером діабету). Мій лікар сказав, що це новий стандарт, оскільки останнім часом діабет зростає, але я не повинен хвилюватися, тому що я не мав зайвої ваги і був здоровим. Порівняно з режимом тестування, який лише позначає пацієнтів поза двома довірчими інтервалами стандартного відхилення, чи ця нова практика позначення результатів при 100 мг/дл збільшує або зменшує чутливість скринінгу діабету? Збільшує або зменшує його специфічність?

6. Інсульт - це коли кров не досягає частини мозку через непрохідність кровоносної судини. Часто непрохідність обумовлена атеросклерозом - затвердженням/звуженням артерій від накопичення бляшок. Інсульти можуть бути дійсно поганими, тому непогано було б їх передбачити. Недавні дослідження шукали потенційно прогностичний біомаркер, і одне дослідження показало, що серед жертв інсульту був надзвичайно високий рівень ферменту під назвою мієлопероксидаза: середнє значення становило 583 пмоль/л, зі стандартним відхиленням 48 пмоль/л. (Див. Це дослідження: https://www.ncbi.nlm.nih.gov/pubmed/21180247) Припустимо, ми хотіли розробити скринінговий тест на основі цих даних. Щоб гарантувати, що ми спіймали 99,7% потенційних жертв інсульту, який діапазон рівнів мієлопероксидази повинен отримати «позитивний» результат тесту? Якщо середній рівень мієлопероксидази серед здорових людей становить 425 пмоль/л, при стандартному відхиленні 36 пмоль/л, приблизно який відсоток здорових людей отримає позитивний результат від запропонованого нами скринінгового тесту?

7. Я опитую вибірку 1,000 американців (припустимо, що це репрезентативно), і 43% з них повідомляють, що вони вірять, що Бог створив людей у їхньому теперішньому вигляді менше 10 000 років тому. (Див. Це опитування: http://www.gallup.com/poll/27847/Maj...Evolution.aspx) На рівні довіри 95%, який діапазон, в якому істинний відсоток, ймовірно, лежить?

8. Члені-волонтери «Матері проти п'яного водіння» провели опитування «від дверей до дверей» в гуртожитку коледжу в суботу ввечері та виявили, що студенти п'ють і в середньому два алкогольні напої на тиждень. Які причини сумніватися в результатах цього опитування?